
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Восстановления давления без учета притокаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод восстановления давления применяют в условиях проявления в пласте упругого режима. Такие условия возникают при остановках, пусках и изменениях режима эксплуатации скважины.
Если в скважине, длительно эксплуатируемой на установившемся режиме, мгновенно изменить дебит на величину
где
Значения Формула (6.1) широко применяется в подземной гидродинамике и называется основной формулой упругого режима фильтрации. В случае, когда наблюдение за изменением давления после мгновенного изменения дебита скважины производить не в какой-либо удаленной точке пласта, а непосредственно на ее забое, то в формулу (6.1) вместо
Формула (6.2) позволяет рассчитать изменение давления на забое скважины при пуске ее в работу с постоянным дебитом на упругом режиме фильтрации. Рассмотрим первую схему исследования, рис.6.2. По условию первой схемы исследования мгновенное прекращение притока жидкости можно представить как наличие отрицательного дебита, равного по величине предыдущему. Тогда, если скважина, работавшая на установившемся режиме с дебитом
или
Формула (6.4) является основой так называемого метода Хорнера. На практике используется тогда, когда время работы скважины Это уравнение прямой в координатах
По углу наклона этой прямой к оси абсцисс
Экстраполируя прямолинейный участок до пересечения с осью ординат, находим пластовое давление Аналогично по формуле (6.3) определяем текущую депрессию
Если
Это уравнение прямой в координатах
По углу наклона этой прямой к оси абсцисс 1. Гидропроводность пласта:
2.Относительная пьезопроводность пласта:
3. Если известны толщина пласта
и проницаемость пласта
4. Если рассчитать пьезопроводность пласта по формуле:
где
6. Если известна статическая депрессия на пласт
где 6. Зная функцию
где 7. Вычисляется общее несовершенство вскрытия пласта – скин-фактор
8. Рассчитывается коэффициент продуктивности скважины на данном режиме:
9. Вычисляется функция
10. Рассчитывается время стабилизации режима,
Факторы, влияющие на характер кривой Восстановления давления
Применение расчетных формул (6.1, 6.2) основано на следующих допущениях: 1. Пласт однородный и бесконечный; 2. Жидкость малосжимаемая; 3. Влияние соседних скважин пренебрежительно мало, так что скважину можно считать единственной в пласте; 4. До возмущения скважина находилась в стационарном состоянии. В реальных условиях эти допущения могут не выполняться, что приводит к искажению формы КВД. К числу причин, наиболее сильно искажающих форму кривых восстановления, следует отнести: 1. Нарушение режима работы скважины перед ее остановкой; 2. Влияние границ пласта; 3. Нарушение геометрии потока в призабойной зоне скважины (скин-эффект); 4. Приток жидкости в ствол скважины после ее остановки; 5. Неизотермичность процесса восстановления давления. Все эти факторы искажают или начальные, или конечные участки кривых восстановления давления.
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 , то давление в любой точке пласта, отстоящей от центра скважины на расстоянии
, то давление в любой точке пласта, отстоящей от центра скважины на расстоянии  , начнет изменяться в соответствии с формулой:
, начнет изменяться в соответствии с формулой: , (6.1)
, (6.1) - изменение дебита скважины;
- изменение дебита скважины;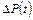 - изменение давления в произвольной точке наблюдения;
- изменение давления в произвольной точке наблюдения; - гидропроводность пласта;
- гидропроводность пласта; - время, отсчитываемое с момента изменения режима скважины;
- время, отсчитываемое с момента изменения режима скважины; - расстояние до точки наблюдения;
- расстояние до точки наблюдения; - коэффициент пьезопроводности пласта;
- коэффициент пьезопроводности пласта; -символ интегрально-показательной функции аргумента
-символ интегрально-показательной функции аргумента  .
.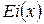 определяются по табл., прил. 1.
определяются по табл., прил. 1. . При этом аргумент
. При этом аргумент  уже через несколько секунд становится очень малым по абсолютному значению. Заменяя интегрально-показательную функцию ее выражением для малого аргумента, найдем депрессию, отсчитываемую от забойного давления:
уже через несколько секунд становится очень малым по абсолютному значению. Заменяя интегрально-показательную функцию ее выражением для малого аргумента, найдем депрессию, отсчитываемую от забойного давления: . (6.2)
. (6.2)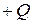 в течение времени
в течение времени 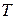 будет остановлена, то остаточная депрессия
будет остановлена, то остаточная депрессия 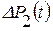 у стенки скважины согласно формуле (6.2) равна:
у стенки скважины согласно формуле (6.2) равна: (6.3)
(6.3) . (6.4)
. (6.4)
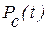 и
и 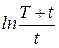 , рис. 6.3.
, рис. 6.3. . (6.5)
. (6.5)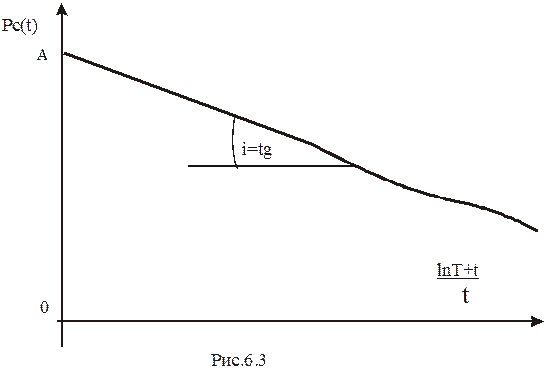
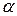 определяется гидропроводность пласта
определяется гидропроводность пласта 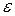 :
: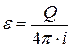 , или
, или  (6.6)
(6.6) .
.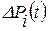 :
: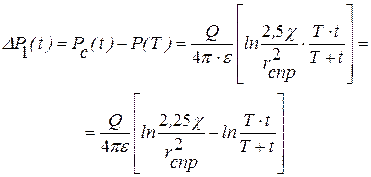 . (6.7)
. (6.7) , то
, то 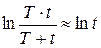 . Отсюда находим формулу обработки кривой восстановления давления после мгновенной остановки скважины, работающей с постоянным дебитом
. Отсюда находим формулу обработки кривой восстановления давления после мгновенной остановки скважины, работающей с постоянным дебитом  :
: . (6.8)
. (6.8)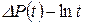 :
: . (6.9)
. (6.9)
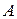 , отсекаемому на оси ординат, см. рис.6.4, определяются следующие параметры пласта.
, отсекаемому на оси ординат, см. рис.6.4, определяются следующие параметры пласта.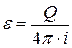 ;
; 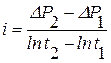 . (6.10)
. (6.10) . (6.11)
. (6.11) и вязкость нефти
и вязкость нефти  , то зная
, то зная 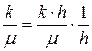 (6.12)
(6.12) :
: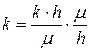 . (6.13)
. (6.13) , (6.14)
, (6.14)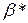 -упругоемкость пласта, то можно вычислить приведенный радиус скважины:
-упругоемкость пласта, то можно вычислить приведенный радиус скважины: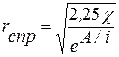 . (6.15)
. (6.15) , то можно вычислить функцию
, то можно вычислить функцию  :
: , (6.16)
, (6.16)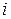 определена по КВД в координатах
определена по КВД в координатах  , можно вычислить приведенный радиус скважины
, можно вычислить приведенный радиус скважины 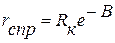 , (6.17)
, (6.17) .
.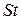 :
: . (6.18)
. (6.18) . (6.19)
. (6.19)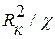 :
: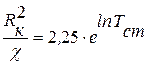 . (6.20)
. (6.20) , ч, по формуле:
, ч, по формуле: . (6.21)
. (6.21)


