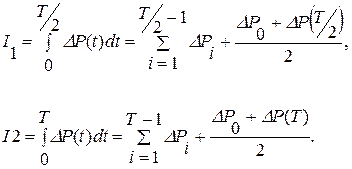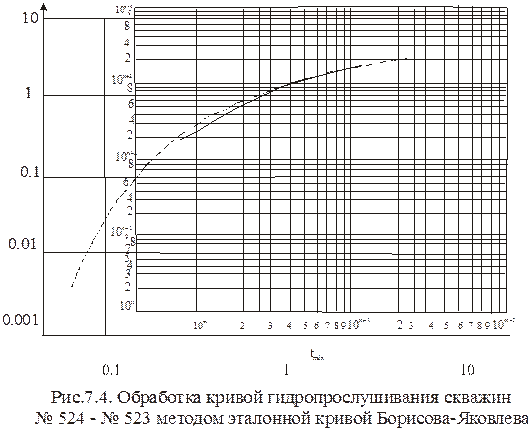Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реагирования С.Н.Бузинова, И.Д.УмрихинаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как видно из (7.4), функция Таким образом, чтобы сделать более заметным импульс, нужно увеличить Одним из методов, позволяющих определять параметры пласта не по отдельным точкам, а по характеристикам, вычисленным по всему участку кривой, является аналитический метод Бузинова - Умрихина. Формула (7.1) в упрощенном виде для условий бесконечного пласта может быть представлена в виде:
Проинтегрируем уравнение (7.7):
Обозначим
Подставляя принятые обозначения в (7.8), получим:
Левая часть выражения (7.9) представляет площадь, ограниченную кривой реагирования и осью абсцисс, рис.. Разделим левую и правую части равенства (7.9) на
Значения величин Имея кривую изменения давления в реагирующей скважине, находим площадь, ограниченную этой кривой и осью абсцисс. Разделим эту площадь на площадь прямоугольника
а по формуле найдем пьезопроводность пласта:
Иногда, для облегчения расчетов коэффициент пьезопроводности может быть найден по номограмме, см. рис. 7.8. Этот метод дает удовлетворительные результаты, если кривая реагирования имеет гладкий вид. При обработке негладких кривых реагирования функция Предлагаемый ниже метод обработки свободен от этих недостатков.
7.1.3. "Метод площадей" для обработки кривых реагирования (метод Р.И.Медведского и К.С.Юсупова)
Сущность "метода площадей" заключается в использовании всей кривой реагирования в виде отношения площадей первого цикла одно кратного импульсирования, см. рис. 7.1. Расчетная формула этого метода:
где
Функция справа зависит только от
Функция затабулирована. Значения Имея кривую реагирования однократного импульсирования по площадям Тогда по формулам:
или
определяются коэффициенты пьезопроводности и гидропроводности пласта. 7.1.4. Практические примеры
Рассмотрим практические примеры применения методов гидропрослушивания при однократном импульсировании.
На рис.7.1 приведена кривая изменения давления в простаивающей скважина № 1 Мегионского нефтяного месторождения. Кривая реагирования обработана пятью разными графоаналитическими методами, а результаты приведены, табл. 7.1. Сущность аналитических методов обработки кривых реагирования состоит в вычислении площадей, ограниченных кривой реагирования и осью абсцисс. Эти площади могут быть найдены непосредственно планиметрированием или любым из способов численного интегрирования. Обычно при малом шаге разбиения кривой реагирования удовлетворительные результаты дает метод трапеции. Для расчета площадей
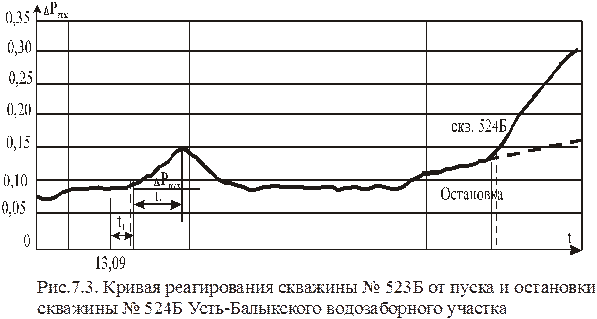
На рис. 7.3 представлен график изменения давления водозаборной скважины № 5236 Усть-Балыкского участка в зависимости от остановки скважина № 524. Как видно, см. рис. 7.3, между скважинами № 5246 и № 5236 по водоносному пласту сеноманского возраста имеется хорошее взаимодействие. Кривая реагирования обработана методом эталонной кривой Борисова-Яковлева, рис.7.8, а результаты приведены, табл. 7.1.
Таблица 7.1 Обработка результатов гидропрослушивания
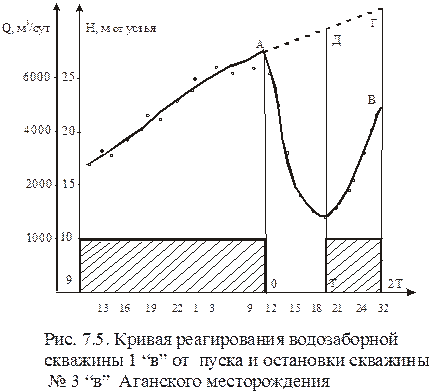
На рис. 7.5 представлен график реагирования уровня водозаборной скважины № 1в от остановки и пуска возмущающей скважины № 38 Аганского водозаборного участка. Обработка кривой проведена методом измерения площадей – планиметрированием. № 12 Русского месторождения высоковязкой нефти от пуска и от остановки закачки воды в пласт нагнетательной скважина № 40. Кривая реагирования получена с помощью дистанционного датчика давления типа ДД-8 и обработана методом площадей.
На рис. 7.6 приведена кривая реагирования простаивающей скважина. Результаты обработки методами однократного импульсирования приведены, см. табл. 7.1.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.009 с.) |

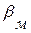 в правой части монотонно возрастает, поэтому чем больше
в правой части монотонно возрастает, поэтому чем больше 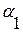 , тем больше
, тем больше 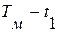 , тем больше, чем меньше
, тем больше, чем меньше 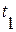 , и с этой целью последнее как будто нужно устанавливать более коротким. Однако это не совсем верно, поскольку значительно уменьшается
, и с этой целью последнее как будто нужно устанавливать более коротким. Однако это не совсем верно, поскольку значительно уменьшается 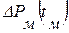 , а импульс может быть вообще не замечен в реагирующей скважине.
, а импульс может быть вообще не замечен в реагирующей скважине.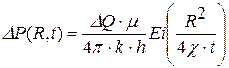 . (7.7)
. (7.7)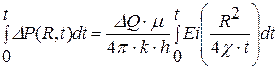 . (7.8)
. (7.8)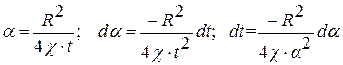 .
.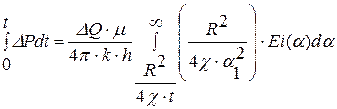 . (7.9)
. (7.9)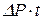 с учетом (7.7), имеем:
с учетом (7.7), имеем: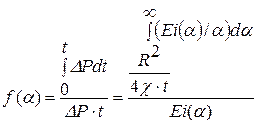 . (7.10)
. (7.10)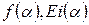 даны, прил. 5.
даны, прил. 5.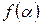 . По таблице прил.5, найдем численные значения величин
. По таблице прил.5, найдем численные значения величин 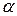 и
и 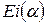 , тогда пьезопроводность
, тогда пьезопроводность 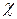 вычислим по формуле:
вычислим по формуле: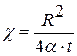 , (7.11)
, (7.11)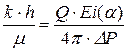 . (7.11¢)
. (7.11¢)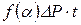 в виде площади прямоугольника зависит от точки на кривой реагирования. Если положение точки определено на дефектном участке, то площадь прямоугольника определяется с погрешностью.
в виде площади прямоугольника зависит от точки на кривой реагирования. Если положение точки определено на дефектном участке, то площадь прямоугольника определяется с погрешностью.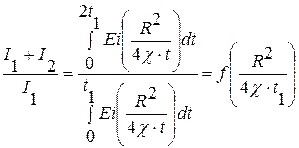 , (7.12)
, (7.12)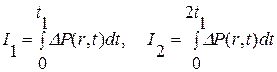 .
.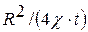 и является универсальной. Обозначив функцию справа через
и является универсальной. Обозначив функцию справа через 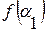 , где
, где 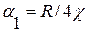 ;
; 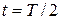 , получим более удобную для использования формулу:
, получим более удобную для использования формулу: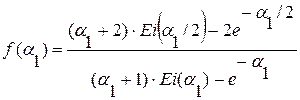 . (7.13)
. (7.13)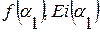 приведены,прил. 2.
приведены,прил. 2.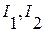 определяем
определяем 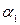 и
и 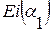 .
.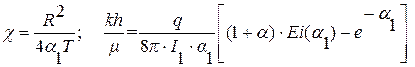 (7.14)
(7.14)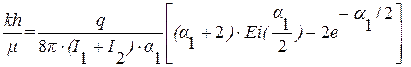 (7.15)
(7.15)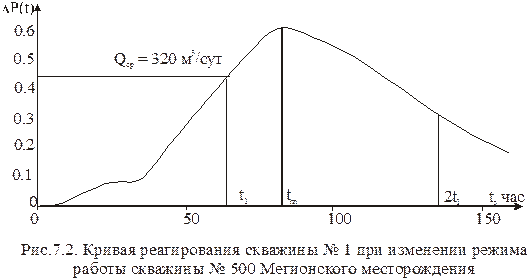
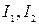 методом трапеции рекомендуются формулы
методом трапеции рекомендуются формулы 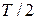 .
.