
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы обработки кривых восстановления давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С учетом притока
Промысловые исследования показали, что немгновенное закрытие скважины на забое иногда настолько сильно деформирует кривую восстановления давления, что для выхода этой кривой на асимптоту требуется много времени. Поэтому с целью сокращения времени исследования скважин и использования информации начальных участков КВД были предложены методы их обработки с учетом притока. Текущий затухающий приток жидкости из пласта в скважину определяют непосредственно с помощью глубинных дебитомеров или косвенно, путем вычисления по формуле:
Суммарный приток или количество жидкости, поступившей из пласта в скважину после ее остановки можно найти по формуле:
Затухающий приток жидкости из пласта в скважину можно вычислить и по формуле:
где
Формулы (6.32) и (6.33) получены в предположении, что приток в скважину после ее остановки происходит за счет заполнения труб и затрубного пространства, т.е. объема скважины, занятого газом – жидкостью, которая продолжает поступать из пласта в скважину. Формулы справедливы для случая мгновенной сепарации газа в насосно-компрессорных трубах и основаны на предположении, что процесс в скважине после остановки изотермический. Фактически не мгновенная сепарация газа в фонтанных трубах, а также перераспределение температуры в стволе скважины приводит к тому, что приток жидкости определяется не только ростом давления на забое за счет восстановления давления в пласте после остановки скважины, но и сепарацией газа, и перераспределением температуры по стволу скважины. Влияние этих факторов иногда приводит к получению немонотонных кривых притока. Применение глубинных дебитомеров – расходомеров позволяет исключить погрешности, связанные с неточностями определения притока в скважину после ее остановки. В настоящее время разработано множество методов обработки КВД с учетом притока в дифференциальной и интегральной модификации. Все эти методы теоретически достаточно обоснованы, но отличаются точностью и сложностью вычислений. В основу обработки КВД с учетом притока положены уравнения: 1. Для дифференциального метода:
2. Для интегрального метода:
где График в координатах Из основных формул (6.35 и 6.36) можно вывести расчетные формулы почти всех дифференциальных и интегральных методов обработки КВД. Например, если приближенно принять Целый ряд методов обработки КВД основан на формуле:
Это методы Пирвердяна ( Ю.П. Борисов для приближенного вычисления
При остановке скважины, работавшей кратковременно в период
При тех же значениях
При
Устремляя
что полностью совпадает с интегральным методом И.А. Чарного и И.Д. Умрихина. Для практического вычисления среднего геометрического времени
здесь под Как видно, в формулах (6.45) и (6.46) единственную трудность представляет вычисление сингулярного интеграла типа:
И.А. Чарным и И.Д. Умрихиным был предложен способ прямого вычисления интеграла методом прямоугольников. Немного позже Ю.П. Борисов представил другой, значительно более простой способ вычисления (6.45), основанный на аппроксимации подынтегральной функции квадратичной параболой (6.40) и (6.41). Нами в работе обобщен способ Ю.П. Борисова. Подынтегральная функция аппроксимируется не одной, а четырьмя различными квадратичными параболами, а затем среди полученных приближений выбирается наилучшее. Для практического вычисления сингулярного интеграла Tf, с учетом оценки погрешностей, принято следующее приближение:
где
Погрешность расчетов по формулам (6.48) и (6.49) в сравнении с точными методами не превышает 6 %. На основании вышеизложенного предлагается для обработки КВД с учетом притока дифференциальный метод:
и интегральный метод:
где
Разбивая промежуток интегрирования
Значение сингулярного интеграла
Кривая восстановления давления в системе координат Отметим, что предложенные дифференциальный и интегральный методы обработки КВД с учетом притока по точности не уступают методу И.А. Чарного и И.Д. Умрихина и намного проще в вычислениях. На рис. 6. 16 приведен пример обработки КВД с учетом притока по скважине № 4 Вынгинской площади. Как видно из рисунка, КВД без учета притока выходит на асимптоту через 3,5 часа, а КВД с учетом притока с самого начала прямолинейная.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.008 с.) |

 . (6.32)
. (6.32) . (6.33)
. (6.33)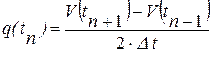 , (6.34)
, (6.34) - соответственно площади затрубного пространства и насосно-компрессорных труб по внутреннему диаметру;
- соответственно площади затрубного пространства и насосно-компрессорных труб по внутреннему диаметру;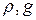 - плотность жидкости, поступающей в скважину;
- плотность жидкости, поступающей в скважину;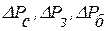 , - соответственно текущая депрессия на забое, в затрубном пространстве и на буфере скважины.
, - соответственно текущая депрессия на забое, в затрубном пространстве и на буфере скважины. , (6.35)
, (6.35) , (6.36)
, (6.36) , (6.37)
, (6.37) - геометрическое среднее время по давлению или дебиту для дифференциальных методов;
- геометрическое среднее время по давлению или дебиту для дифференциальных методов; 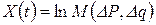 - геометрическое среднее время по давлению или дебиту для интегральных методов.
- геометрическое среднее время по давлению или дебиту для интегральных методов.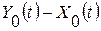 или
или  прямая линия. По ее наклону и точке пресечения с осью давлений можно найти гидропроводность
прямая линия. По ее наклону и точке пресечения с осью давлений можно найти гидропроводность  кh/m и относительную пьезопроводность
кh/m и относительную пьезопроводность  пласта.
пласта. , то получим метод поправочного коэффициента. Этот метод был предложен в 1953 г. Глетферьтром и Уэлси, а позже проверен на гидроинтеграторе Требиным и Щербаковым в 1955 г.
, то получим метод поправочного коэффициента. Этот метод был предложен в 1953 г. Глетферьтром и Уэлси, а позже проверен на гидроинтеграторе Требиным и Щербаковым в 1955 г. , (6.38)
, (6.38) ), Блинова (
), Блинова ( ), Гусейнова (
), Гусейнова ( ) и др.
) и др. предлагает аппроксимировать
предлагает аппроксимировать  или
или  на участке
на участке  параболой второй степени:
параболой второй степени: ; (6.39)
; (6.39) . (6.40)
. (6.40) с постоянным дебитом
с постоянным дебитом  , параметры пласта по КВД могут быть определены дифференциальным методом Ю.А. Мясникова / /. В основе этого метода используется прямолинейная анаморфоза вида:
, параметры пласта по КВД могут быть определены дифференциальным методом Ю.А. Мясникова / /. В основе этого метода используется прямолинейная анаморфоза вида: . (6.41)
. (6.41)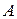 ,
, 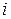 и переменной
и переменной 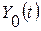 , что и в методе Ю.П.Борисова, но с иным определением координаты
, что и в методе Ю.П.Борисова, но с иным определением координаты  :
: (6.42)
(6.42)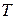
 и
и  метод преобразуется в дифференциальный метод И.А. Чарного и И.Д. Умрихина, не учитывающий продолжительность работы скважины до остановки T. Дифференциальный метод, приближенно учитывающий продолжающийся приток, дает заниженные (до 30%) параметры пласта. И.А. Чарный и И.Д. Умрихин предложили один из первых интегральных методов. В обобщении Ю.А. Мясникова с учетом кратковременной работы скважины в течение времени
метод преобразуется в дифференциальный метод И.А. Чарного и И.Д. Умрихина, не учитывающий продолжительность работы скважины до остановки T. Дифференциальный метод, приближенно учитывающий продолжающийся приток, дает заниженные (до 30%) параметры пласта. И.А. Чарный и И.Д. Умрихин предложили один из первых интегральных методов. В обобщении Ю.А. Мясникова с учетом кратковременной работы скважины в течение времени  формула этого метода имеет окончательный вид (6.41), причем переменные
формула этого метода имеет окончательный вид (6.41), причем переменные  и
и  выражаются следующим образом:
выражаются следующим образом: (6.43)
(6.43) и учитывая, что
и учитывая, что 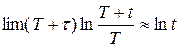 получим более простое выражение:
получим более простое выражение: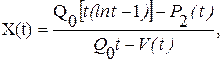 (6.44)
(6.44)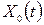 и
и  представим их в общем виде:
представим их в общем виде: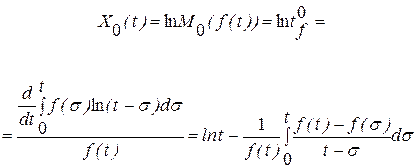 ; (6.45)
; (6.45) , (6.46)
, (6.46) понимаем
понимаем  или
или  .
.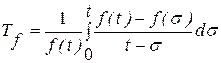 . (6.47)
. (6.47)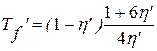 ; (6.48)
; (6.48) ; (6.50)
; (6.50) . (6.51)
. (6.51) (6.35)
(6.35) (6.36)
(6.36) - импульс давления;
- импульс давления; 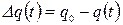 - потерянный дебит;
- потерянный дебит; − потерянная добыча;
− потерянная добыча; 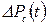 - забойная депрессия;
- забойная депрессия; - установившийся дебит скважины до остановки;
- установившийся дебит скважины до остановки;  - медленно-затухающий приток жидкости;
- медленно-затухающий приток жидкости; - накопленный приток жидкости.
- накопленный приток жидкости. и
и  - дебит, численно равные площади, ограниченной кривой
- дебит, численно равные площади, ограниченной кривой  и
и 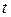 , могут быть вычислены любым из методов численного интегрирования, например, по формуле трапеции.
, могут быть вычислены любым из методов численного интегрирования, например, по формуле трапеции. на n частей, получим:
на n частей, получим: . (6.37)
. (6.37) и
и  может быть определено по графику, рис.6.16.
может быть определено по графику, рис.6.16.
 или
или  прямая линия. По наклону этой прямой к оси абсцисс
прямая линия. По наклону этой прямой к оси абсцисс  .
.


