
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Св-ва капельных ж-тей и газовСодержание книги
Поиск на нашем сайте
Св-ва капельных ж-тей и газов Капел.э-ть отличается тем, что в малых V за счет сил.поверх.натяжения принимают форму капли,а в больших образуют свободную пов-ть контактирующую либо с либо с атмосф. Воздуом либо с газом.1. текучесть – спос-ть ж-тей и газа изменять форму под действием сколь угодно малых сил. 2 вязкость – св-во обратное текучести, спос-ть Ж. или Г. Сопрот-ся смещению др.слоев при их совместном дв-ии. Проявл-ся только при движении. К-т кинемат.вязкости ϧ(мю)(м2/с). К-т динамич.вязкости µ(Па*с). ϧ=
Силы действующие в ж-тях и газах. 1 массовые илиобъемные – силы пропорциональные массе и равномерно распределенные по объему-силы тяжести и силы инерции переносного движ-ия. 2поверхностные – силы пропорциональные площади пов-ти и равномерно распред-ные по ней(пов-ые силв в Ж и Г вызывают напряжение-давление) P=F/S па. Н=(кг*м)с2
Св-ва гидростатич.давления 1) не зависит от ориентировки площадки и всегда направлена по внутр.нормали. т.к. ж-ть обладает текучестью, то если бы Р действовало не по нормали, то оно бы вызывало силу действующую не по нормали, раскладывающуюся на нормальную и тангенсиальную составляющую то тангенц. Составл-щая всегда обнуляется (благодаря текучести) и остается одна нормальная составляющая.2)гидростатическое Р в любой точке ж-ти по всем направлением одинаково. В неподв-ной ж-ти выберем точку. Свяжем с ней начало координат. В окр-ти этой точки построили 3хгранную призму с бесконечно малыми ребрами. Изнач-но полагаем что в направ-нии каждой из осей действует своя вел-на давления Рх, Ру, Рz. В напралении плоскости dn действует Рп. Каждая вел-на давления опр-ся силой в направ-ии соотв-щей оси и площади соотв-щей площадки. Составим усл-ия равн-сия призмы в направ-ии оси Х.
Ос-ное ур-ие гидростатики Рассмотрим ж-ть в резервуаре в статичском состоянии на свободную пов-ть ж-тей действует Ро-атмосф-ное давление.в ж-ти выделим вертик.цилиндр. с бескон. Малой площадью dS и конечной высотой – h, вес -G Т.к. ж-ть нах-ся в равновесии—и цилиндр нах-ся в равновесии принимая, что в обл-ти нижнего торца цил-ра ж=дейситвует Р составим условие равновесие в направлении верт. Оси. –
Диф.ур-ия равновесия Эйлера В иссл-ой ж-ти выберем точку М свяжем с началом коор-т в окр-ти построим пар-пипед с бесконечно малыми ребрами. В общем случае равнов-ия жид равнод-ющая массовых сил – R не направлена вертик. Вниз т.к. могут сущ-ть силы инерций переносного дв-ия. Т.е. дв-ие ж-ти совмесно с резервуаром, т.е с выбранной системой коор-т. Разложим R на оси. Введем понятие единичной массовой силы- силе относительной к массе. тогда обозначим елиничные сост-ия равнод-щей на ссответствующей оси X=
6 основное ур-ие гидростатики из ур-ия Эйлора. Каждая из системы диф.ур-ий равновесия Тейлора Х на дХ ду и дz и все три уравнения сложим. Xdx+Ydy+Zdz – 1/ρ
7. основные понятия и опр-ия гидрогазодинамики. В общемслучае параметры дв-ия зависят от t.однако,бывают случаи,когда изменение пар. Равновремени либо незначительная либо изменение параметров отн=но t имеет циклич.х-р с малыми вличинами отклонения, либо можно считать,что параметры вообще не зависят от t. Такое дв-ие или режим течения н-ся установившемся илистационарным. В случае когда параметры дв-ия яв-ся ф-цией времени то такое течение или режим дв-ия н-ся н еустановившемся, нестационарным. В движущихся Ж или Г, Р обладает теми же св-вами, что и при их статическом состоянии т.е. в любой точке по всем направлением давления одинаково и оно направлено всегда по внутр. Нормам. В отличии от дв-ия тв.тел при дв-ии Ж или Г набл-ся различие скоростей дв-ие отдел. Частиц на-ся в одном поперечном сечении потока.это обусловлено силами трения.,возникающимим м-у движущейся средой и ограничивающими стенками., а также силами трения внутри Ж и Г определяемыми вязкостью среды. Если в поперечном сечении любого потока каждой отдельно взятой движущейся частице построить вектор скорости, затем концы векторов соединить плавной кривой то получится распределение скоростей поперечном сечении потока – поле скоростей. В ламинарном р-ме дв-ия профиль поля скоростей имеет вид правил.параболы. линии тока – кривая в каждой точке которой вектор скорости направлен по касательной. Установивемся р-ме дв-ия линия тока совпадает с траекторией.если в потоке выделить несколько малый замкнутый контур и в каждой точке этого контра провести линии тока то получится трубч.пов-ть – трубка тока. поток внутри трубки тока н-ся = элементар.стркйкой в устан. Р-ме дв-ия эл.струйка обладает след. Св-вами:1)форма струйки с течнием времени неизменна 2)границы элем.струйки непроницаемы для с теч. Времени для ж-ти наход=щйся в сосед.струйках. 3) все частицы движущейся среды в попер.счении эл.струйки имеют одинаковую скорость, т.е. профиль поля скоростей в поперечном сечении эл.струйки имеет вид прямоугольника.совокупность все элементарных струек н-ся потоком. при дв-ии капельных ж-тей различают потоки напорные и безнапорные.. в напорны потоках ж-ть занимает все поперечное сечение магистрали.. в безнапорных потоках ж-ть занимает часть только часть попер.сечения магистрали с образ-ем своб.пов-ти контактирующей либо с атм.воздухом, либо с каким то другим газом. Безнапорных газовых потоков не сущ-ет. Живое сечение потока-это s сечения потока проводимого номрально к направлению линий тока. В потоке капельной ж-ти вводится понятие смоченный периметр – это весь или часть периметра живого сечения по которому ж-ть контактирует с ограничивающими ее стенками. Гидравл.радиус - отношение S живого сечения к смоченному периметру.Rт=d/4. Методы описания дв-ия ж-ти Сущ-ют 2 метода описания движ-ия ж-ти: 1) метод Лагранжа -в этом методе изучается дв-ие отдел. Частиц вдоль траектории. 2) метод Э йлора. В этом методе изучаются параметры движ-хся частиц в фиксированной точке пространства, то составляют ур-ия дв-ия и опис-ся изм-ием параметров ф-циии от скоорости и времени. Если считать что основными параметрами хар-щие движ-щие силы яв-ся скорость и Р то функцион.связь этих параметров будт иметь вид Vx=f(x,y,z,t), Vy… Vz..также.
Диф. Ур-ия дв-ия Ж и Г Диф. Ур-ия дв-ия можно получить из диф.ур-ий равновесия если к действующим силам добавить силы инерции.в диф.ур-иях равновесия исп-лись единичные силы, т.е. силы отнесенные к массе, поэтму необ-мо добавить силы инерции так же тнесенные к массе. Примеч.: в соотьветсвии с 2 зак-ном F=ma a=F/m. Cистема диф.ур-ий равновесия записана для 3- х коор-т поэтому необх-мо добаить в каждое ур-ие вел-ну ускорения в напраление соответствующей оси. X-à 11 ур-ие неразрыности – ур-ие расхода. Анализ капельной Ж и Г показыает, что межмолекуулярные промеж-ки в этих средах различны при\чем в газах брольше что и обуславливает их бесконечную сжимаемость.в капельных ж-тя эти пром-ки практически отсутствуют пожтому они обладают низкой сжимаемостью к-рая в свою очередь объясняется сжимаемостью растворенного в ж-тя газа.поэтому эти срелы особенно газообразные яв-ся дискретными,т.е. несплошными.поэтому для описания св-ви поведления таки сред необходим мат.аппарат базирующийся на спец.ф-циях что знач-но усложнякт решение практически задач.ур-ие неразрыности яв-ся мат.выражением з-на сохранения для для массы дв-ия газа ил ж-ти в гипотезе их сплошности.рассмотрим уч-к элементарной струйки перемнной площадью попереяного сеченияв произв-но расположенной в пространстве м-у с ечениями 1 и 2. Пксть за бесконечно малый промежуток времени dt масса Ж и Г нах-ся м-у 1 и 2 перемемтится в положением-у сечениями 1” и 2”. Анализ показ-ет что перемещение всей массы в-ва идентично перемещению масы из положения м-у сечениями 1-1” в положение м-у 2 и 2”. Считаем что в каждом из началыьных чечений 1-2) были соотв. Параметры дв-ия ρ1ds1*v1dt=p2ds2v2dtàp1ds1v1=p2ds2v2т.к. сечение в эл-ной струйке выбраны пароизв-но то можем записать что pidsivi=const=dQm. Кг/c – массовый расхожд.расходом н-ся кол-во в-вапроодящего через поперечное сечение потока в ед-цу времени. Для вычисления массового расода вего потока ур-ие необ-мо проинтегрироватьпо пдощади поперечного сечении приче при интегрировании будем считать что скорочть дв-ия капельглй ж-ти dQmViSi=Q м3/cм где Qm объемный расход. Qm=Qρ Qg=Qpg. V1s1=v2s2=Q=const. v1v2/s2s1.скорочть дв-ия ж-ти обратно пропорциональна величине площади поперечного сечения. На практике скорость зависит от диаметра трубы, т.е. от приращения площади.
Гидравл.потери Как показывает опыт величина энергет.потерь дв-ия ж-ти поропорциональная. В целях упрощения опр-ия Г.п. их принято делитьна 2 вида:1)потеря на трение потеря на длине, путеые потери-потери связанные с преодолением сил трения. 2) потери на преодоление местны сопротивлений. Под местными сопротивлениями понимается уч-к магистрали, преодоление которого нужен допол.затрат энергии к ним относится: любые геометрич.искажения, магистралирастяж.сужение поороты) а также любая гидр.потерч клапан, распред-тель фильтр кран вентиль).
Р-мы течения ж-ти и газа Наа опыте устан-но чято при дв-ии ж-ти и газа при разл.усл-ия может сущ-ть разл.физ.нормы течения. Ламинарный р-м –ся спокойным слоистым дв-ием без переливания и без пульсации давления и скорости. Турбулентный р-м х-ся интенсивным переливанием слоев, т.е. обменом энергии м-у отдел. Частицами образованием отрывых и виревых зон течения. Ж-ть склонна к ламинар.дв-ию при малых скоростях. Осборн уст-ил что вел-ну критической скорости дв-ия при которой происодит смена реж-мов дв-ия можно опред-ть по ф-ле Vкр= К1гню)/d где ню-к=т кин.вязкости К=(Vкр*d)/ϧ =Re кр. Длч крупных ассиметричных труб Ку rh gjcnjzyyf/ lkz dct[;-ntq b ufpf = 2300/ xbckj Reопределяет р-м дв-ия ж и г. Если ре меньше 2300 то ламинар. Если больше то турб. При неперерыном увеличении скорости дв-ия среды начиная от 0 и при достижении Re =2300 начинает зарождаться яв-ие турбулентности развитие которыхх может продолжаться до 4000. Т.е. этот уч-к в диапазоне 2300-4000 яв-ся переходным. Однако на практике его считает турбулентным, из=за сложности расчетов различных факторов влияющих на режим течения. Потери на трении в лам.р-ме Ранее п=была получен зав-ть hтр= Pтр/pg. Найдем величину потерь на трение используя зав-ть для опр-мя расхода.
Т.к. потери на трение в любом р-ме дв-ия ж-ти можно опр-ть по ф-ле Дарси вецсбоха
Турбулентнт. Р-м дв-ия(ТРД) Т.к. в ТРД сущ-ют пульсации Р-ия и скорости тоо строго говоря ТР не яв-ся установившемся (стационарым). Однако как показывает опыт пульчсации давления и скорости осущ-ся относ-но некоторы вел-н, к-рые с течением времени ост-ся неизменными потому ТР рассматривают как стационарный парасетры которого будут зависеть от числа Re потока. Иначе говря с развитием ТР т.е. с ростом числа ре несколько меняется физ.картина течения—0>меняется –р энергетического обмена м-у отдельными движ-ся частицами что и опред-ет физ. Парасетры потока. В частности к-т кореолиса альфа в ТР зависит от интенсивности турб.яв-ий т.е. от числа рейнольдса потока.
Кк видно из графика с уеличением ре альфа уменьшается или убываает приближаясь к 1. Потому при выпаолнении приближенных практических расчетов турб.течений можно применить альфа турб=1. Поскольку на –р дв-ия ж-ти или газа в турб.дв-ии влияет множ-во факторов теретическиф учеки к-рых часто затруднен. потому на практике при опрд-ии различных вел-н ар-щи турб. Течение испол-ся имперические или полуимперические зав-ти. Имперические – получены на основе экспер.данных. полуимперические – получены теорет.путем и уточненные разл. К-тами., полученными по р0-там ксперимента. В частности теорет.зав-тей для определения к-та потерь на трение Л(лямда)турбулентное не сущ-ет. На практике пользуются зав-тями полученными разл. Авторами,, хорошо работающие,, при определенных усл-ях(различная ж-ть, числа Re. Известна ф-ла конакова полученная для числа Rе кр меньшего числа Re и меньшего 6*
Для гидравлически гладки тркб исп-ся ф-ла Блазиуса Гидравлически гладкими трубами н-ся такие у к-ры высота микронеровносте пов-тей мала и она не оказывает влияние на вел-ну потерь на трение.(трубы из стекла сцв.Ме, сплавов нержавеющей стали полимерны мат-лов).наибольшее применение на практике получила ф-ла дл опр-ия к-та потерь на трение:Л(лямда)- Альтиция. - для шероховатых труб Рис.
Потери на трение в диф-ре зависят от его длины,что опр-ся углом α и ст-нью расширения n.Исп-уя формулу Вейзбаха для определения потерь на трение была получена эмпирическая зависимость для опр-ия коэф-та потерь на трение.hтр=(λтр/8sin(α/2))*(1-1/n2)(v1/2g)2.Потери св-ые с расширением потока можно вычислить по формуле Вейзбаха используя коэф-нт потерь опред-ый для внезапного расширения потока.Но т.к.условие расширения в диф-ре мягче,то исп-ся коэф-нт смягчения к<1.В р-те потери на рассм.в диф-ре:hрасш=к*(1-S1/S2)2*v12/2g.Подставляя значения в (*)=>hдиф=[λтр/8sin(α/2)(1-1/n2)+k(1-S1/S2)2]v12/2g.(выражение в кв-ых скобках- ᶓдиф)на практике:α(5-20)0;k=sinα;Если представить графики зависимостиь коэффициента потерь ф-ии от α. Рис.
Ф-ия имеет выр-ый экстремум в районе значения α=60,т.е. при этих углах полураствора гидравлические потери на диф-ре минимальны.Это объясняется тем,что при малых углах полурастворвора α<60 диф-ор получается длинным и в нем преобладают потери на трение;при α>60 диф-ор ->короткий ->потери на трение снижаются,но возрастают потери св-ые с расширением потока.hдиф=ᶓдиф*(v12/2g) Рис.
26)гидравлические потери при внезапном сужении русла:При внезапном сужении маг-ли набсяпоявление 2-х отрывных зон течения,происходит преврашение потенциальной энергии в кинетическую и потери опр-ся по формуле Вейсбаха......... Коэффициент потерьна внезапном сужении -по формле Идельчика........................ рис.
В частном случае внезапного сужения труба отходит от резервуара больших размеров:S1>>>S2,тогда S2/S1-->0, ᶓв суж=0,5 рис. допонителное сопротивление->расход уменьшается. 27)гидравлические потери при внезапном и плавном повороте канала: hотв= ᶓотв*v2/2.Коэффициент потерна отводе опр-ся по формуле Некрасова следующего вида: ᶓотв=0,051+0,19*d/R.При вычислении потерь на отводе не опр-ся потери на трение на нем эти потери учит-ся при опр-ии потерь на всей длене трубопровода рис. 28)истечение жидкости в атмосферу через отверстие в тонкой стенке:о.в.т.с.-наз-ся такое у которого диаметр во много больше толщины стенки. Рис.
При выходе из отв-ия струя истекающей жидкости с увеличением скорости,что можно оценить коэффициентом сжатия струи.ε=Sc/S0=(dc/d0)2; Z1+(P1/pg)+(α1v1/2g)= Z2+(P2/pg)+(α2v2/2g)+сумма(h1-2);Z1=H;Z2=0;v1=0; сумма(h1-2)=ᶓ*v22/2g; P1=P2=P0; H=α2v2/2g+ ᶓv22/2g;=>v2=((H*2g)/(α2+ ᶓ))1/2; ϕ=1/(α+ᶓ)=>v=ϕ*(2gH)1/2; СЛУЧАЙ ИДЕАЛЬНОЙ ЖИДКОСТИ:
29)истечение сжимаегого газа через отверстие в тонкой стенке при малых перепадах давления:
30)истечение жидкости через насадок при постоянном напоре:насадком наз-ся короткая труба не более 6- ти диаметров.Пусть жидкость из резервуара вытекает через насадок в аnмосферу. рис.
При входе в насадок струя несколько сжимается затем расширяясь занимает все поп-ое сечение насадка.Если составить ур-ие Бернулли выбрав в качестве 1-ого сечения свободную пов-сть жидкости в рез-ре,а в качестве второго сечения на выходе из насадка,то можно получить те же самые ур-ия для опред-ия скорости истечения и расхода используя все те же обозначения:v=ϕ(2gH)1/2;Q=µS0(2gH)1/2.Однако т.к. коэффициент сжатия на выходе из насадка=1,то µmax=εϕ=0,8=ϕ.т.е. при всех прочих равных условиях расход при истечении через насадок по сравнению с расходом истечения через отверстие в тонкой стенке больше в 1,3раза: µнас/µт.с.=0,8/0,6=1,3.Это объясняется тем,что в сечении 1-1 внутри насадка,где обр-ся отрывная зона течения реализуется давление ниже атмосферного(вакуум).И эта область играет роль своеобразного вакуумного насоса”помогающего”истечению жидкости из резервуара,причем давления в 1-1 и 2-2 связаны зависимостью:P1=P2-0,75pgH.Из уравнения видно,что:1)т.к.давление P2=Pатм то P1 в абс-ой шкале всегда меньше атмосферного.2)с ростом напора H давление P1 снижается т.е. возрастает величина вакуума. При этом при некотором значениях H=Hкрит=13,5м.(вода),атм-ое давление сжимает струю отрывая ее от стенок и атм-ый воздух прорывается в область пониж-ого давления,при этом реализуется истечение(истечение с отрывом)аналогичное ист-ию через отв-ие в тонкой стенке при этом расход падает т.к.µ из 0,8->0,6.При обратном снижении напора H возврат к безотрывному режиму ист-ия происходит при величинах напора значит уменьшается критическая.Это явление наз-ся явление Гистеррезиса режимов истечения т.е. при напорах H<Hкрит равноправно могут сущ-ать 2 режима с отрывом и без отрыва,что яв-ся серьезным препядствием при проектировании гидравл-их систем. 31)уравнение движения идеального сжимаегого газа.Интеграл Бернулли:Ранее рассм-ись ур-ия давления в формуле Эйлера справедливое как для капельной жид.,так и для сжимаемой.dvx=x-(1/p)*(dP/dx)(и так для y и z) Все слагаемые в ур-ях представляют собой единичные ситы,т.е. силы отнесенные к массе.Рассматривая сжимаемый газ можно видеть,что массовые силы к которым относятся-тяжести и инерции малы по ср-ию с дин-ими силами и силами давления и ими можно пренебреч(x=y=z=0).Тогда система диф-ых уравнений движения для сжимаемого газа принимает вид –dvx/dt=-(1/p)*(dP/dx)(для у и z).Преобразовав эти ур-ия умножив и разделив левые части на dx,dy,dz получаем-(dvx/dx)*(dx/dt)=-(1/p)*(dP/dx) и т.д.;Если считать движение установившимся для которого учтановившееся соотношение vx=dx/dt(y,z); (dvx/dx)*vx=-(1/p)*(dP/dx)(y,z);dvxvx=-(1/p)*(dP/dx)*dx(y,z).Сложим уравнения:vxdvx+vydvy+vzdvz—(1/p)*((dP/dx)dx+(dP/dy)*dy+(dP/dz)*dz)=>d(v2/2)+dP/p=0;интеграл((dP/p)+v2/2)=const(*).Уравнение (*) наз-сят интегралом Бернулли и это ур-ие уст-ет связь между пар-ами газа в установившемся режиме движения.Для вычисления интеграла(dP/p)-необходимо знать зависимость плотности от давления.На практике эта зависимость опр-ся при измерении следующих допущений:1)газ считается идеальным.2)течение адиабатным,т.е.без теплообмена с окр-ей средой.3)течение-одномерное т.е.параметры движения газа меняются только по одной координате совп-щей с напр-ем движения. 32)элементы термодинамики,используемы при рассмотрении газовых потоков.: среди гипотез приеняемых при рассмотрении газовых потоков яв-ся гипотеза об идеальности газа для которого параметры св-ны ур-ем сост.идеального газа или ур-ем Менделеева-Клапейрона:PV=mRT,Pv=RT,v=V/m=1/p;R=RM/M(RM-универсальная газовая пост.)[Дж/кг*К-кельвин]В термодинамике среди мн-ва сущ-их процессов рассм-ся изо-процессы т.е. простейшие т.е. протекающие при постоянстве к-л параметра:-изохорный(V-const);изобарный(P-const);изотермический(T-const);адиабатический(изоэнтропный)-(S-const)(энтрапия)-без теплообмена с окр-ей средой.При рссмотрении движ-ия идельного газа частопримен-ся гипотеза об адиабатности этого процесса т.е.отсутствия обмена энергией с окр-ей средой.Из термодинамики известно,что адиабатный процесс опис-ся 3-мя уравнениями Пуассона или ур-ями адиабатыидеального газа:Pvk=const,Tvk-1=const,TPk-1/kconst(k-коэффициент Пуассона или показатель адиабаты определяемйы выражением-k=Cp/Cv(теплоемкости при p и v-const)Cp-Cv=R-уравнение Майера. ДЛЯ ВОЗДУХА k=1,4. В результате при рассмотрении движ-ия газа часто исп-ся 4 основные гипотезы:1)течение одномерное(пар-ры изм-ся только по 1-ой координате)2)течение установившееся (параметры не изменяются во времени)3)течение изоэнтропное(без теплообмена с окр.средой)4)движущ-ся газ-идеальный(ур-ие сост.идеального газа справедливо) 33)АЛГЕБРАИЧЕСКИЙ ВИД ИНТЕГРАЛА БЕРНУЛЛИ ДЛЯ ОДНОМЕРНОГО УСТАНОВИВШЕГОСЯ ИЗОЭНТРОПНОГО ТЕЧЕНИЯ ИДЕАЛЬНОГО ГАЗА: интеграл(dP/p)+v2/2=const.Выполняется одним из уравнений адиабаты Pvk-const т.к. v(удельный объем)=1/p;P/pk-const=C=>P=Cpk(1);dP=Ckpk-1dp/:p;dP/p=Ckpk-2dp;Проинтегрируем уравнение,предварительно подстаив С из(1).интеграл(dP/p)=Pk/pk(k-1) *pk-1=kP/(k-1)p. Интеграл Бернулли:k/k-1*P/p+v2/2=const.С читая газ идеальным Pv=RT,P/p=RT=>k/k-1*RT+v2/2=const;k/k-1*RT=(k--1)/(k-1)RT+1/(k-1)*RT используя ур-ие сост-ия идеального газа последнее ур-ие:P/p+v2/2+1/k-1*RT=const.Последнее ур-ие пок-ет,что при изоэнтропном течении ид-ого газа сумма пъезометрического и скоростного и теплового напоров вдоль координаты движения есть величина постоянная.Из ур-ия видно,что в потоке газа возможен переход части мех-ой энергии в тепловую и обратно,при сохранении постоянства суммы всех видов энергии т.е. это ур-ие яв-ся мат-им выражением закона сохр-ия энергии движения ид-ого газа. 34)СЖИМАЕМОСТЬ ГАЗОВ.СКОРОСТЬ РАСПРЕДЕЛЕНИЯ ЗВУКА В ГАЗЕ:В отличае от капельной жидкости любой газ обладает сжимаемостью т.е. способностью изменять свой объем при внешних возд-ях.Из изики известно что мерой сжимаемости физ-их тел яв-ся скорост распределения звука в этом теле.Скорость звука в тв-ых телах больше чем скорость звука в жидких и больше чем скорость звука в газах.(приложение уха к рельсам).СКОРОСТЬ ЗВУКА В ВОЗДУХЕ=340м/c.Обозначим vзв=а.a2 =lim ///////=dP/dp=>a=(dP/dp)1/2;в абсолютно несжимаемой среде а->00.Рассмотрим vcpdдля изоэнтропного движения идеального газа.P/pk-const=C=>P=Cpk;dP=Ckpk-1dp.dP/dp=Ckpk-1=Pkpk-1/pk=k*P/p=>a=(k*P/p)1/2=(kRT)1/2.Скорость распределения малых возм-ий в газе т.е. скорость звука зависит от давления,плотности и температуры газа.При решении практических задач с движущимся газом обычно используют не абсолютную скорость движения газа,а скорость отнесенную к скоростьи звука(а).M=v/a(число маха потока).v<a M<1(дозвуковой поток;v=a M=1(звуковое течение);v>a M>1(сверхзвуковое течение).Рассмотрим физ-ую картину движения газа или тел с физ.телами:1)v=0 M=0;2)v<a M<1;3)v=a M=1;4)v>a M>1; рис.sina=dt/vt=a/v;1/M;M=1/sina;
Выразим отношение P/p:a=(k*P/p)1/2;a2=k*P/p*P/p=a2/2; k/k-1*a2/k+v2/2=const--с ростом скорости движения газа (а)скорость звука уменьшается и наоборот. 35)ОЦЕНКА ВЛИЯНИЯ СЖИМАЕМОСТИ ГАЗА НА ХАР-КИ ТЕЧЕНИЯ: При решении практ. задач иногда необходимо ответить на вопрс при каких условиях влиянием сжимаемости газа на хар-ки течения и параметры можно пренебреч:k/k-1*P/p+v2/2=const-интеграл Бернулли в алг-ой форме.Если предположить,что газ истекает из резервуара в котором его скорость v=0,то исходя из уравнения Бернулли параметры газа будут иметь величины соответствующие неподвижному,т.е. заторможенному потоку.Обозначим параметры заторможенного потока (параметры торможения)через величины P0,p0,v0,T0=0,тогда уравнение Берулли можно записать в виде:............................................................................................. Считая газ идеальным и течение изоэнтропным можем записать ур-ие адиабаты:............................................
Если рассмотреть атмосферный воздух к=1,4,то подставляя числа маха=>..................... Из табл.видно,что при скоростях движения по числу М до 0,3 изменение плотности потока не превышает 5%, что укладывается в погрешность изм-ых приборов в эксперименте поэтому на практике при скоростях газа не превышающих 30% от скорости звука в этом газе влиянием сжимаемости т.е. изменением плотности пренебрегают. 36)ОСНОВНЫЕ СООТНОШЕНИЯ ДЛЯ ОДНОМЕРНОГО,УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ ИДЕАЛЬНОГО ГАЗА: Используя параметры заторможенного потока с помощью ур-ия Бернулли их можно связать с текущими пар-ами потока:.......................................
Величина дельта Т ук-ет на педение темп-ры при скорости движения v или иначе говоря эта величина ни что иное как прирост t тела при торможении газа начиная с какой-то скорости v.На практике эта величина дельта Т будет несколько меньше т.к. любое течение не яв-ся изоэнтропным,т.е. часть энергии движущ-ся газа рассеивается в окр-ей среде.Если рассмотреть атм-ый воздух к=1,4;R=287Дж/кгК:дельта Т=v2/2000;По этой причине аппараты возвращающиеся с орбиты Земли с большими скоростями сильно разогреваются.Разделим 2 часть уравнения на Т:....................................................................................... Восп-ся ур-ями адиабаты следующего вида......................................
Используя уравнение (*) и полученное соотношение запишем:........................................ Система уравнений А уст-ет связь между текущими параметрами потока и пар-ами торможения этого же потока ф-ии от числа маха.Из ур-ий видно,что с ростом v движения газа т.е. с ростом числа маха потока давление,плотность и t потока снижается. 37)КРИТИЧЕСКИЕ ПАРАМЕТРЫ ПОТОКА;Запишем ур-ие Бернулли............... Как было ук-но ранее и видно из этого ур-ия с ростом скорости движения газа скорость звука уменьш-ся,т.е. в заторможенном потоке когда скорость газа=0 скорость звука имеет макс.значение и т.к. при непрерывном увеличении скорости движ.газа,начиная от 0 скорость звука уменьшается начиная с макс.значения,то обязательно по координате дв-ия сущ-ет сечение потока в котором скорость дв-ия газа=скорости звука в этом газе.Это сечение наз-ся критическое сечение и параметры газа в этом сечении наз-ся крит-ими параметрами обозначаемые:................... рис.
Используя (А) и подставляя в нее число маха=1:....................... Свяжем с помощью ур-ия Бернулли пар-ры заторможенного потока и пар-ры в критическом сечении:..........
скорость звука в заторможенном потоке...........................................скорость звука в крит-ом сечении:aкр=vкр.
38)МАКСИМАЛЬНАЯ СКОРОСТЬ ПОТОКА:при помощи ур-ия Бернулли сведем параметры заторможенного потока и текущие его параметры......................................... Из уравнения видно,что максимальное значение скорости будет соответствовать Т=0,v=vmax....................... Иначе говоря максимальное значение v истечения будет опр-ся величиной темп-ры торможения потока,v близкую к максимальной можно получить при истечении в вакууме когда понижать давление в движ-ся газе можно практически до 0.На практике получить vист=vmax незьзя,т.к. сущ-ют энергические потери и точение не адиабатное.......................................... В ракетной технике стремясь получить максимальную скорость истечения продуктов сгорания различными способами пытаются увеличить t горения топлива,т.е. поднять t заторможенного потока однако рак-ые дв-ия относящиеся к химическим тепловым движениям имеют ограничения по применимости по выше упомянутым причинам.Теоретическое значение максимальной скорости истечения газа соответствует переходу всей внутренней энергии газа в кинетическую. 39)БЕЗРАЗМЕРНАЯ СКОРОСТЬ ИЛИ КОЭФФИЦИЕНТ СКОРОСТИ.....ЕГО СООТНОШЕНИЕ С ЧИСЛОМ МАХА ПОТОКА:Наряду с числом маха потока М=v/a в газодимамических расчетах исп-ся безразмерная скорость...=v/aкр,где акр-кр-ая скорость звука акр=(кRTкр)1./2.Свяжем между собой число маха и безразмерную.............
Отношение температур в полученном выражении найдем используя ур-ия из систем уравнений (А и Б)......
Анализ ур-ия показывает,что при числах М<1...<1,не=М;M=0,....=1;M>1,....>1,не=M;Изуравнения видно,что при увеличении М.....-осимптотически приближается....................если взять атмосферный воздух к=1,4,то.................. РИС
Если уравнение (*) решить относительно числа маха М и подст-ить в сист (А).......................
40)ЗАВИСИМОСТЬ МЕЖДУ ПЛОЩАДЬЮ ПОПЕРЕЧНОГО СЕЧЕНИЯ СТРУИ И СКОРОСТЬЮ ГАЗА.УРАВНЕНИЕ ГЮГОНИО:Используем 4 гипотезы:1)течение одномерное 2)течение установленное 3)течение идеальное 4)газ идеален.Запишем уравнение неразрывности в форме массового расхода в направлении оси ОХ..............................................
исключим из этого уравнения 1-ое слагаемое исп-уя 1-ое ур-ие из системы диф-ых ур-ий дв-ия Эйлера.dvx/dt=-1/p*dP/dx-считая,что течение одномерное в направлении оси Х...............................................т.к.течение установившееся........................... Одновременно запишем:.................................. подставим значение в уравнение нер-ти записанное в диф-ой форме............. перепишем ур-ие одновременно опуская при скорости индекс Х,т.к.течение одномерное..............................
Полученное уравнение-уравнение Гюгонио уст-ющее связь между площадью поп-ого сечения потока и его числом маха.М<1 в этом случае (1-М2)>0,чтобы выполнилось равенство необходимо,чтобы изменение S и v были разнонаправленны т.е.при уменьшении S,dS<0=>dv>0(v увеличивается)и наоборот.М>1=>(1-M2)<0 т.е. S и v имеют разные знаки.М=1 течение звуковое (1-М2)=0,dS=0 dv=0.S=const,v=const(крит-ое течение).Для непр-ого увеличения v газового потока необходимо чтобы S сначала уменьшилась и при дост-ии vдвиж=vзв. Критическое-с минимальной S (v=a,M=1) рис.
Канал перп-ой S обеспечивающий напр-ое увеличение v от дозвуковых к сверхзвуковым наз-ся геометрическим соплом давления.В соответствии с системой уравнений А при неопр-ом увеличении v движения газа т.е. с увеличением числа маха потока давление,плотность и температура-уменьшатся. рис. 41)АНАЛИТИЧЕСКАЯ ЗАВИСИМОСТЬ ПЛОЩАДИ ГАЗОВОЙ СТРУИ ОТ ЧИСЛА МАХА ПОТОКА: Для выявления зависимости площади поп-ого сечения каналаот числа маха потока восп-ся ур-ем неразрывности в форме массового расхода связав текущие параметры с параметрами в критическом сечении................ ........................... Используем зависимость для определения скоростей звука:.......................... для искл-ия разм-ыхпараметров в ур-ии считая течение изоэнтропным восп-ся одним из уравнений адиабаты идеального газа:...................... ...................... Для исключения из уравнения отношения температур и перехода к безразмерным величинам восп-ся уравнениями из системы А и Б.......................... .......................................... Графически зависимость имеет вид: рис.
Из графика видно,что одно и то же отношение площадей соответствует 2-м числам маха в до и сверхзвуковых областях сопла Лаваля. 42)РЕЖИМ РАБОТЫ СВЕРХЗВУКОВОГО ГЕОМЕТРИЧЕСКОГО СОПЛА ЛАВАЛЯ: Как ук-ось выше из системемы уравнения А следует,что с ростом скорости движения газа параметры потока давление плотности потока убывают,т.е. по длине всего сопла Лаваля давление непрерывноснижается(т.к.v увелич-ся).Если истечение газа из сопла Лаваля происходит в какое-то пространство заполненное каким-либо газом или в атмосферу,то в зависимости от того как соотн-ся между собой давление окр-ей для сопла газа-PH и давление на выходе из сопла,т.е. на его срезе Pa различают 3 режима работы соплы Лаваля: рис.
1)в том случае когда Pa/PH=1-расчетный режим истечения яв-ся наивыгоднейшим с точки зрения энергетических характеристик сопла,а применительно к реактивному дв-ию соплоработающее в расчетном режиме позволяет получит максимальную величину реактивной силы(тяги двигателя);2)PH>Pa,Pa/PH>1-режим с перерасширением т.е. поток перерасширился и давление стало менше давления окр-ей среды;3)PH<Pa,Pa/PH>1-режим с недорасширением,т.е. можно было бы удлинит сверхзвуковую часть сопла,чтобы поток расширялся в сопле до давления окружающей среды. В случае работы сопла режима с перерасширением когда давление на срезе уменьшается давление окружающей среды при определенных соотношениях Pa и PH струя может оторваться от стенок сверхзвуковой части сопла -->сопло работает с отрывом потока,что энергетически не выгодно.При стационарном режиме работы сопла давление на срезе-неизменно и в случае изменения давления окр.среды (ракета в атмосферу)изменяется режим работы сопла от расчетного к недорасширению. рис. 43)УДАРНЫЕ ВОЛНЫ И СКАЧКИ УПЛОТНЕНИЯ.ПРЯМОЙ СКАЧЕК УПЛОТНЕНИЯ: Как следует из уравнения Гюгонио торможение сверхзвуковых потоков происходит при уменьшении площади поп-ого сечения канала.Однако вся практика сверхзвуковых течений связана ударными волнами или скочками уплотнения.Ударная волна и
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.156.91 (0.019 с.) |

 . С ростом температуры вязкость ж-ти уменьшается, а с ростом давления возрастает. 3. сжимаемость –способность изменять V под действием внешних сил.газы обладают сжимаемостью. Капельные ж-ти обладают низкой сжимаемостью к-рую можно оценять при помощи к-та низк сжатия βv=-
. С ростом температуры вязкость ж-ти уменьшается, а с ростом давления возрастает. 3. сжимаемость –способность изменять V под действием внешних сил.газы обладают сжимаемостью. Капельные ж-ти обладают низкой сжимаемостью к-рую можно оценять при помощи к-та низк сжатия βv=- 
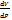 знак – обусловлен тем что с ростом давления объем уменьшается. 4 растворимость газов в ж-тях -спос-ть ж-ти растворять газ. Хар-ся количеством раств-ого газа в ед-це объема ж-ти с ростом t растворимость газов снижаться. С ростом Р растворимость повыш-ся. Для упрощения решения задачь введено понятие ид-ных Ж и Г к-рые счит-ся абс. Невязкими а ж-ть абс. несжимаемой
знак – обусловлен тем что с ростом давления объем уменьшается. 4 растворимость газов в ж-тях -спос-ть ж-ти растворять газ. Хар-ся количеством раств-ого газа в ед-це объема ж-ти с ростом t растворимость газов снижаться. С ростом Р растворимость повыш-ся. Для упрощения решения задачь введено понятие ид-ных Ж и Г к-рые счит-ся абс. Невязкими а ж-ть абс. несжимаемой Rx-Rncosα=0 Px dzdy-Rn dydncosα=0 Px-Pn=o Px=Pn.
Rx-Rncosα=0 Px dzdy-Rn dydncosα=0 Px-Pn=o Px=Pn.  Rz-Rnsinα=0 Pz dxdy-Pn dydnsinα. Pz-Pn=0 Pz=Pn
Rz-Rnsinα=0 Pz dxdy-Pn dydnsinα. Pz-Pn=0 Pz=Pn -G+F=0 -
-G+F=0 -  P=P0+pgh-осн.ур-ие гидростатики. С пом. К-рого можно опр-ть Р в любой точке ж-ти зная Р в др. точке этой ж-ти и рас-ие м-у этими точками, измеренное по вертикали. Пренебрегая изменениям плотности и ускорения своб.падения от высоты h можно считать что Р в жиж. Есть лин.ф-ция от высоты. Тогда эпюра Р на вертикальную стенку рез-ра будет иметь форму треугол. Из этого ур-ия видно что на одной глубине Р равны. Пов-ть в каждой точке которой давление одинаково-пов-ть уровня.
P=P0+pgh-осн.ур-ие гидростатики. С пом. К-рого можно опр-ть Р в любой точке ж-ти зная Р в др. точке этой ж-ти и рас-ие м-у этими точками, измеренное по вертикали. Пренебрегая изменениям плотности и ускорения своб.падения от высоты h можно считать что Р в жиж. Есть лин.ф-ция от высоты. Тогда эпюра Р на вертикальную стенку рез-ра будет иметь форму треугол. Из этого ур-ия видно что на одной глубине Р равны. Пов-ть в каждой точке которой давление одинаково-пов-ть уровня. ,Y=Ry/m, Z=Rz/m.-à Rx=Xm, Ry=Ym, Rz=Zm. Пусть в окр-тя М действуетдавление Р.тогда направление в каждой из осей
,Y=Ry/m, Z=Rz/m.-à Rx=Xm, Ry=Ym, Rz=Zm. Пусть в окр-тя М действуетдавление Р.тогда направление в каждой из осей +
+  =0. Выражение в квадрат.скобках предст.собой полный диф-л ф-ции.тогда ур-ие принимает вид:Xdx+Ydy+Zdz-
=0. Выражение в квадрат.скобках предст.собой полный диф-л ф-ции.тогда ур-ие принимает вид:Xdx+Ydy+Zdz-  =0 dP=ρ(Xdx+Ydy+Zdz)-ф-ция давлений.рассмотрим частный случай, когда перенос дв-ия отсутствует, тогда ос-ся только одна массовая сила-сила тяжести направлнная верт-но вниз., т.е. составляющих равнодействующей на оси Х и У нет. Х=У=0. dP=ρZdz. Т.к. по 2-у з-ну Ньютона, сила отнесенная к массе это ускорение,а сл-но z=-g, где z-это ускорение свободного падения g. Знак – обусловлен разнонаправленностью оси и ускорения. dP=-ρgdz. Ρg-const. P=-ρgz+C Z=
=0 dP=ρ(Xdx+Ydy+Zdz)-ф-ция давлений.рассмотрим частный случай, когда перенос дв-ия отсутствует, тогда ос-ся только одна массовая сила-сила тяжести направлнная верт-но вниз., т.е. составляющих равнодействующей на оси Х и У нет. Х=У=0. dP=ρZdz. Т.к. по 2-у з-ну Ньютона, сила отнесенная к массе это ускорение,а сл-но z=-g, где z-это ускорение свободного падения g. Знак – обусловлен разнонаправленностью оси и ускорения. dP=-ρgdz. Ρg-const. P=-ρgz+C Z=  P=
P= 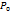
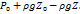 P=P_0+ρgh-осн.ур-ие гидростатики.
P=P_0+ρgh-осн.ур-ие гидростатики.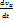 также для у и z. тогда система диф.ур-ий дв-ия примет вид
также для у и z. тогда система диф.ур-ий дв-ия примет вид 
 cистема диф. Ур-ий дв-ия Эйлера. Физ.смысл – полное ускорение частицы вдоль коор-т осей склад-ся из ускорения массовых сил и сил Р. Система ур-ий спраедлива как для сжимаемой и несжимаемой ж-ти, так и для установивш. И неустан.режимов дв-ия
cистема диф. Ур-ий дв-ия Эйлера. Физ.смысл – полное ускорение частицы вдоль коор-т осей склад-ся из ускорения массовых сил и сил Р. Система ур-ий спраедлива как для сжимаемой и несжимаемой ж-ти, так и для установивш. И неустан.режимов дв-ия




