
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идентификация характеристик технологических объектов с использованием стандартных методов ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Суть и этапы регрессионного анализа Регрессионный анализ заключается в определении аналитического выражения связи зависимой случайной величины Y (называемой так же результативным признаком) с независимыми случайными величинами X1, X2,…Xm (называемыми так же факторами). Форма связи результативного признака Y с факторами X1, X2,…Xm получила название уравнения регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессии (в последнем случае возможно дальнейшее уточнение: квадратичная, экспоненциальная, логарифмическая и т.д.). В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессии. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками – множественной (многофакторной) регрессией. При изучении регрессии следует придерживаться определенной последовательности этапов: 1. Задание аналитической формы уравнения регрессии и определение параметров регрессии. 2. Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии. 3. Проверка статической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.
Основное содержание этапов регрессионного анализа Основное содержание выделенных этапов рассмотрим на примере множественной линейной регрессии, реализованной в режиме «Регрессия» надстройки Пакет анализа Microsoft Excel. Этап 1. Уравнение линейной множественной регрессии имеет вид
где
Параметры уравнения регрессии могут быть определены с помощью метода наименьших квадратов (именно этот метод используется в Microsoft Excel). Сущность данного метода заключается в нахождении параметров модели (ai), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии, т.е.
Рассматривая S в качестве функции параметров ai и проводя математические преобразования (дифференцирование), получаем систему нормальных уравнений с m неизвестными (по числу параметров ai):
где n – число наблюдений; m – число факторов в уравнении регрессии. Решив систему уравнений, находим значения параметров ai, являющихся коэффициентами искомого теоретического уравнения регрессии. Этап 2. Для определения величины степени стохастической взаимосвязи результативного признака Y и факторов X необходимо знать следующие дисперсии: - общую дисперсию результативного признака Y, отображающую влияние как основных, так и остаточных факторов:
где - факторную дисперсию результативного признака Y, отображающую влияние только основных факторов:
- остаточную дисперсию результативного признака Y, отображающую влияние только остаточных факторов:
При корреляционной связи результативного признака и факторов выполняется соотношение
Для анализа общего качества уравнения линейной многофакторной регрессии используют обычно множественный коэффициент детерминации R2, называемый также квадратом коэффициента множественной корреляции R. Множественный коэффициент детерминации рассчитывается по формуле
и определяет долю вариации результативного признака, обусловленную изменением факторных признаков, входящих в многофакторную регрессионную модель. Так как в большинстве случаев уравнение регрессии приходится строить на основе выборочных данных, то возникает вопрос об адекватности построенного уравнения генеральным данным. Для этого проводится проверка статической значимости коэффициента детерминации R2 на основе F -критерия Фишера:
где n – число наблюдений; m – число факторов в уравнении регрессии. Примечание. Если в уравнении регрессии свободный член а0 = 0, то числитель n-m-1 следует увеличить на 1, т.е. он будет равен n-m.
В математической статистике доказывается, что если гипотеза H0: R2 = 0 выполняется, то величина F имеет F -распределение с k = m и l = n-m-1 числом степеней свободы, т.е.
Гипотеза H0: R2 = 0 о не значимости коэффициента детерминации R2 отвергается, если
При значениях R2 >0,7 считается, что вариация результативного признака Y обусловлена в основном влиянием включенных в регрессионную модель факторов X. Этап 3. Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т.е. значения данных коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии наряду с проверкой значимости коэффициента детерминации R2 включает в себя так же и проверку значимости каждого коэффициента регрессии. Значимость коэффициентов регрессии проверяется с помощью t -критерия Стьюдента:
где В математической статистике доказывается, что если гипотеза H0: ai = 0 выполняется, то величина t имеет распределение Стьюдента с k = n-m-1 числом степеней свободы, т.е.
Гипотеза H0: ai = 0 о незначимости коэффициента регрессии отвергается, если Кроме того, зная значение tкр, можно найти границы доверительных интервалов для коэффициентов регрессии:
Для работы с регрессией открываем вкладку Сервис –> Анализ данных –> Регрессия (см. рис. 2.24.).
Рис. 2.24
В диалоговом окне Регрессия задаются следующие параметры: 1. Входной интервал по Y – вводится ссылка на ячейки, содержащие данные по результативному признаку. Диапазон должен состоять из одного столбца. 2. Входной интервал X – вводится ссылка на ячейки, содержащие факторные признаки. Максимальное число входных диапазонов (столбцов) равно 16. 3. Флажок Метки – устанавливается в активное состояние, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок следует деактивировать. В этом случае будут автоматически созданы стандартные названия для данных выходного диапазона. 4. Уровень надежности – установите данный флажок в активное состояние, если в поле, расположенном напротив флажка необходимо ввести уровень надежности отличный от уровня 95%, применяемого по умолчанию. Установленный уровень надежности используется для проверки значимости коэффициента детерминации R2 и коэффициентов регрессии аi. (Уровень надежности оставляем по умолчанию 95 %). 5. Константа-ноль – установите данный флажок в активное состояние, если требуется, чтобы линия регрессии прошла через начало координат (т.е. а0 = 0). 6. Выходной интервал/Новый рабочий лист/Новая рабочая книга. В положении Выходной интервал активизируется поле, в которое необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экране появится сообщение в случае возможного наложения выходного диапазона на исходные данные. В положении Новый рабочий лист открывается новый лист, в который начиная с ячейки А1, вставляются результаты анализа. Если необходимо задать имя открываемого нового рабочего листа, введите его имя в поле, расположенное напротив соответствующего положения переключателя. В положении Новая рабочая книга открывается новая Книга, на первом листе которой, начиная с ячейки А1, вставляются результаты анализа.
Вывод результатов: В первой таблице сгенерированы результаты по регрессионной статистике. Эти результаты соответствуют следующим статистическим показателям:
2. R-квадрат – коэффициенту детерминации R2; 3. Стандартная ошибка – остаточному стандартному отклонению
- Наблюдения – числу наблюдений n.
В следующей таблице сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R2. 1. Столбец df – число степеней свободы. Для строки Регрессия число степеней свободы определяется количеством факторных признаков m в уравнении регрессии Для строки Остаток число степеней свободы определяется числом наблюдений n и количеством переменных в уравнении регрессии Для строки Итого число степеней свободы определяется суммой 2. Столбец SS – сумма квадратов отклонений. Для строки Регрессия – это сумма квадратов отклонений теоретических данных от среднего:
Для строки Остаток – это сумма квадратов отклонений эмпирических данных от теоретических:
Для строки Итого – это сумма квадратов отклонений эмпирических данных от среднего:
3. Столбец MS – дисперсии, рассчитываемые по формуле
Для строки Регрессия – это факторная дисперсия Для строки Остаток – это остаточная дисперсия 4. Столбец Значимость F – значение уровня значимости, соответствующее вычисленному значению Fp.
В последней таблице сгенерированы значения коэффициентов регрессии ai и их статические оценки. 1. Коэффициенты – значения коэффициентов ai. 2. Стандартная ошибка – стандартные ошибки коэффициентов ai.
4. Р-значение – значения уровней значимости, соответствующие вычисленным значениям tp. 5. Нижние 95% и Верхние 95% - соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии ai.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.72.220 (0.013 с.) |

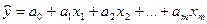 , (2.1)
, (2.1)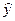 – теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии;
– теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии;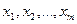 – значения факторных признаков;
– значения факторных признаков;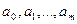 – параметры уравнения (коэффициенты регрессии).
– параметры уравнения (коэффициенты регрессии).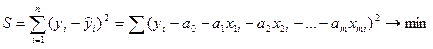 . (2.2)
. (2.2)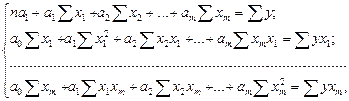 (2.3)
(2.3)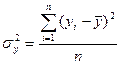 , (2.4)
, (2.4)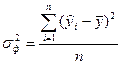 ; (2.5)
; (2.5)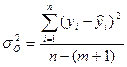 . (2.6)
. (2.6)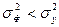 , при этом
, при этом 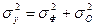 . (2.7)
. (2.7)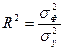 (2.8)
(2.8)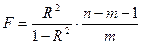 , (2.9)
, (2.9)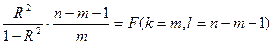 . (2.10)
. (2.10)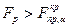 .
. , (2.11)
, (2.11)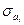 – стандартное значение ошибки для коэффициента регрессии
– стандартное значение ошибки для коэффициента регрессии 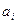 .
.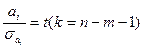 . (2.12)
. (2.12)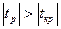 .
.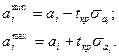 (2.13)
(2.13)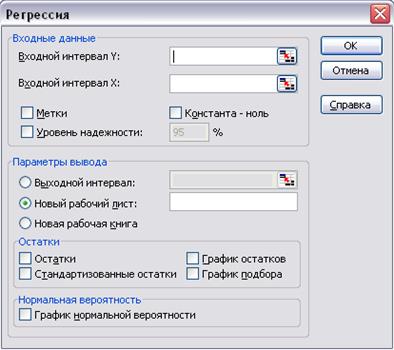
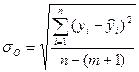 ; (2.14)
; (2.14)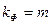 .
.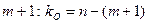 .
.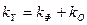 .
.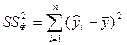 . (2.15)
. (2.15)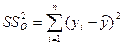 . (2.16)
. (2.16)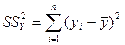 или
или 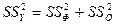 . (2.17)
. (2.17)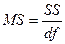 . (2.18)
. (2.18)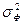 .
.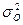 .
.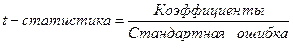 (2.19)
(2.19)


