
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика анализа режимов тепловых сетей на основе макромоделированияСодержание книги
Поиск на нашем сайте
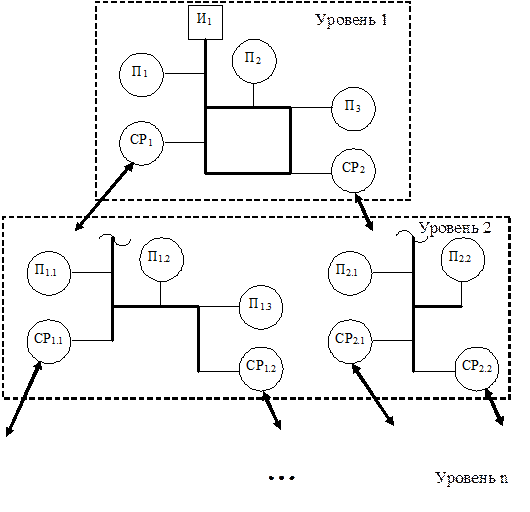
Решение задачи оперативного анализа экономичности режимов функционирования тепловых сетей осуществляется на основе математического моделирования процесса теплоснабжения. Для эффективного моделирования системы теплоснабжения в реальном времени требуется разработка упрощенной макромодели тепловой сети, не требующей чрезмерной детализации характеристик сети и позволяющей проводить расчет и анализ режимов теплоснабжения с достаточной для практического применения точностью. Суть предлагаемого подхода состоит в представлении реальной тепловой сети в виде многоуровневой структуры с выделенными сетевыми районами, отдельными крупными потребителями и соединяющими их магистральными тепловыми сетями (рис. 5.2). В отличие от полной модели, отражающей состояния всех имеющихся межэлементных связей, в макромодели отображаются состояния значительно меньшего числа межэлементных связей, что соответствует описанию объекта при укрупненном выделении элементов. В основу построения макромодели для расчета тепловых сетей могут быть положены следующие принципы: 1. Сетевые районы (СР i) со сложной схемой сетевых соединений, содержащие большое количество относительно маломощных потребителей, рассматриваются как единый эквивалентный потребитель. 2. Потребители (П j), подключенные непосредственно к магистральной сети, рассматриваются как таковые. 3. При необходимости более подробного рассмотрения параметров гидравлических режимов внутри отдельных сетевых районов может быть осуществлен переход на следующий уровень макромодели, отражающий состояние потребителей (П i.k) и вновь выделенных сетевых районов (СР i,j) внутри сетевого района СР i. При этом объект СР i, являющийся потребителем на верхнем уровне макромодели, выступает в роли источника для сетевого района СР i j.
На основе указанных выше принципов реализуется возможность использования при анализе одной и той же тепловой сети нескольких моделей, различающихся сложностью, точностью и полнотой отображения свойств. Таким образом, в зависимости от целей моделирования может изменяться степень детализации представления и описания модели тепловой сети. При этом следует отметить, что результаты однократно выполненного трудоемкого моделирования отдельного сетевого района могут многократно применяться далее в укрупненной общей макромодели, что обуславливает общее снижение объема вычислений.
Рис. 5.2. Многоуровневая структура тепловой сети
Применение на практике математической макромодели тепловой сети, описанной выше, в составе автоматизированной системы диспетчерского управления позволяет оперативно анализировать функционирование систем теплоснабжения в различных режимах и повысить надежность и экономичность процесса теплоснабжения. Рассмотрим методику построения математической макромодели тепловой сети. Основными элементами, образующими систему теплоснабжения, являются источники, обеспечивающие притоки транспортируемой среды и привносящие энергию в систему, абонентские теплопотребляющие установки (далее: потребители) и тепловая сеть виде совокупности взаимосвязанных трубопроводов, соединяющих источники со множеством потребителей. При математическом моделировании все эти подсистемы находят соответствующее отражение в расчетной топологической схеме сети: участки сети, включающие все местные сопротивления, - в виде ветвей, места расположения источников (притоков) и потребителей (стоков), а также соединения ветвей - в виде узлов (вершин), см. рис. 5.2. В общем случае тепловые сети образуют многокольцевые системы, для которых топологический граф содержит несколько контуров. Для того, чтобы произвести расчет сети, в ее структуре необходимо выделить ветви дерева и хорды. Задача расчета гидравлического режима сети заключается в определении расходов сетевой воды у потребителей и на отдельных участках сети, а также напоров в узловых точках сети и у потребителей. При расчете гидравлического режима тепловой сети исходными данными являются: схема тепловой сети, сопротивления всех участков сети, напоры на подающем и обратном коллекторах источников, а также сопротивления (проводимости) всех потребителей. В простейшем случае структура тепловой сети не содержит хорд и представляет собой разветвленную сеть с одним источником, что соответствует выделенным сетевым районам после декомпозиции на нижнем уровне макромодели. Для гидравлического расчета таких разветвленных тепловых сетей может быть использована разработанная расчетная гидравлическая макромодель сети, представленная на рис. 5.3.
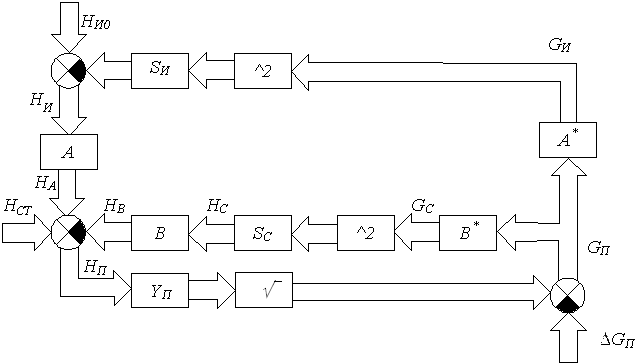
Рис. 5.3. Гидравлическая макромодель разветвленной тепловой сети.
На схеме приняты следующие обозначения: SИ – внутренние сопротивления источников, диагональная матрица n x n, где n – число источников теплоснабжения; SС – гидравлические сопротивления участков сети, диагональная матрица l x l, где l – число участков сети; YП – гидравлические проводимости потребителей, диагональная матрица m x m, где m – число потребителей; НИ0 – напоры источников, когда через них идет нулевой поток, вектор размерности n x 1; НИ, НС, НП – напоры соответственно источников, участков сети и потребителей, векторы размерностей соответственно n x 1, l x 1, m x 1; GИ, GС, GП – расходы соответственно источников, участков сети и потребителей, векторы размерностей соответственно n x 1, l x 1, m x 1; D GП – утечки воды у потребителей, векторы размерности m x 1; HСТ – статический напор на участках сети, вектор размерности l x 1; А, А *, В, В * – матрицы связей, которые задают топологию сети; ^2, √ – операторы возведения в квадрат и взятия квадратного корня элементов векторов. Для расчета гидравлических режимов тепловой сети по предложенной макромодели (рис. 5.3) необходимо составить все перечисленные выше матрицы. Матрица А = {aij} размерности m x n отражает связи между напорами потребителей и источников. Элементы аij матрицы А определяются по следующему правилу: аij = 1, если j -й источник повышает напор по направлению к i -му потребителю, в противном случае аij = -1. Матрица А* размерности n x m отражает связи между расходами потребителей и источников и получена транспонированием матрицы А. Матрица В = {bij} размерности m x l отражает связи между напорами потребителей и участков сети. Элементы bij матрицы В определяются по следующему правилу: bij =1, если j -й участок сети является частью пути к i -му потребителю от какого-либо из насосов, повышающих у него напор, в противном случае bij = 0. Матрица В* размерности l x m отражает связи между расходами потребителей и участков сети и получена транспонированием матрицы В. При известных значениях расходов у потребителей, расчет расходов теплоносителя через узлы осуществляется, начиная с потребителей до источников, и в результате определяются расходы на каждом участке сети и расходы через источники: GС = В*×GП; (5.1) GИ = А*×GП; (5.2) Расчет напоров в узлах сети производится обратным движением от источников, напоры которых известны, к потребителям по соотношению НП = НА – НВ + НСТ; (5.3) где НА = А×НИ; (5.4) НВ = В×НС; (5.5) НИ = НИ0 – SИ×GИ2; (5.6) НС = SС×GС2; (5.7) Сопротивления участков SС определяются по их диаметрам и длинам. Сопротивление участка трубопровода длиной l и диаметром d численно равно потере напора в трубопроводе при расходе воды 1 м3/час и определяется по известным формулам:
где kЭ – эквивалентная шероховатость трубопровода, å x – сумма коэффициентов местных сопротивлений, l – коэффициент гидравлического трения (безразмерная величина), который с достаточной точностью определяется по формуле:
В результате рассчитываются новые значения расходов потребителей:
Задача гидравлического расчета разветвленной тепловой сети может быть решена итерационным методом (например, методом Ньютона) с использованием представленной на рис. 5.3 расчетной макромодели сети по следующему алгоритму: 1. Задается начальное приближение значений расходов потребителей GП0. 2. По расчетной схеме, представленной на рис. 5.3, рассчитываются значения расходов и напоров участков и источников с использованием формул (5.1 - 5.9), а также новые значения расходов потребителей. 3. Найденные значения расходов потребителей GП 1 сравниваются с исходными значениями GП 0. Если разница (GП 1 – GП 0) < e (где e – заданная точность вычислений), то следует перейти к п.5. В противном случае проводится минимизация невязок расчетных расходов GП методом Ньютона или методом простой итерации с релаксацией. 4. Определение новых значений расходов потребителей: GП 0(k +1) = GП 0 (k) + δGП (k), (5.10) и переход к п.2. 5. Конец вычислений. При расчете многоконтурной тепловой сети приведенный ранее расчет деревьев дополняется расчетом хорд. При известных расходах потребителей задаются начальные значения и направления расходов теплоносителя на хордах. В зависимости от выбранного произвольно направления движения теплоносителя на участке, соответствующем хорде, она может выступать как потребитель для одного узла дерева, и как источник расхода - для другого узла дерева. Расчет сетей с хордами проводится при минимизации невязок по расходам на хордах. Преобразование расчетной гидродинамической модели тепловой сети, представленной на рис. 5.3, к виду, изображенному на рис. 5.4, позволяет использовать модель для гидравлического расчета многоконтурных тепловых сетей.
Рис. 5.4. Макромодель многоконтурной тепловой сети
На схеме (рис. 5.4), в дополнение к уже введенным ранее обозначениям, приняты следующие обозначения: GС 1, GС 2– расходы на участках соответственно от потребителей и от хорд, Gh 0– расходы на хордах – вектор-столбцы размерностей соответственно n x 1, l x 1, m x 1; матрицы С размерности m x n и С* размерности n x m определяют соединения участков сети с хордами, а матрицы D размерности m x l и D * размерности l x m отражают связи между хордами и источниками, причем C * = CТ и D * = DТ. Задача гидравлического расчета многоконтурной тепловой сети может быть решена итерационным методом с использованием представленной на рис. 5.4 расчетной модели сети по следующему алгоритму: 1. Задаются начальные значения расходов потребителей GП 0. 2. Задается начальное приближение значений расходов на хордах Gh 0. 3. По расчетной схеме, представленной на рис. 5.4, рассчитываются значения расходов и напоров источников, участков и хорд при постоянных расходах потребителей. 4. Найденные новые значения расходов на хордах Gh 1 сравниваются с исходными значениями Gh 0. Если разница (Gh 1 – Gh 0) < e (где e – заданная точность вычислений), то следует перейти к п. 7. В противном случае проводится минимизация невязок расчетных расходов Gh 0 методом Ньютона. 5. Определение новых значений расходов на хордах: Gh 0(k + 1) = Gh 0 (k) + δGh (k), где k – номер итерации, и далее переход к п. 3. 6. По расчетной схеме, представленной на рис. 5.4, рассчитываются значения расходов и напоров потребителей с учетом рассчитанных в п. 2 – 5 расходов на хордах. 7. Найденные значения расходов потребителей GП 1 сравниваются с исходными значениями GП 0. Если разница (GП 1 – GП 0) < e (где e – заданная точность вычислений), то следует перейти к п. 9. В противном случае проводится минимизация невязок расчетных расходов GП методом Ньютона. 8. Переопределение начальных значений расходов потребителей: GП 0(k +1) = GП 0 (k) + δGП (k), и переход к п.2. 9. Конец вычислений. Таким образом, расчет сети с потребителями происходит с использованием результатов расчета хорд при минимизации невязки расходов на потребителях. Идентификация параметров математических макромоделей При использовании изложенного подхода к моделированию тепловой сети задача идентификации представляет собой задачу определения фактических гидравлических сопротивлений участков тепловой сети и решается на основе расчетной макромодели, представленной на рис. 5.3. В отличие от прямых задач расчета потокораспределения теплоносителя в сети, когда гидравлические сопротивления участков считаются заданными, а напоры Н и расходы G теплоносителя на абонентских вводах потребителей – искомыми, в рассматриваемой задаче идентификации заданными являются измеренные значения статистических наблюдений напоров Н* и расходов G* у потребителей, а также напоры сетевой воды на источниках тепла НИ 0; при этом известна структура сети, т.е. матрицы связей А, А*, В, В*. Выбор располагаемых напоров и расходов теплоносителя на абонентских вводах потребителей тепла в качестве основного источника информации для идентификации обусловливается тем, что это именно те параметры, которые в большинстве случаев контролируются при эксплуатации тепловых сетей. После получения необходимой статистической информации о поведении объекта – тепловой сети формируются функции невязки Ψ выходов модели (НП) и объекта (НП*) следующего вида:
где m - число потребителей; Далее задача параметрической идентификации сводится к задаче поиска минимума целевого функционала на конечном множестве точек tk:
где k – номер измерения параметров гидравлического режима тепловой сети, соответствующий моменту времени tk; N - общее число измерений. Подставляя выражение (5.11) в формулу (5.12), получаем:
Преобразуя выражение (5.13) согласно схеме гидравлической макромодели тепловой сети, приведенной на рис. 5.3, получим следующее выражение для целевого функционала:
где
l - число участков. Целевой функционал является выпуклой функцией, поэтому для решения поставленной задачи оптимизации можно использовать известные методы, например, метод простого покоординатного спуска или градиентный метод. Далее, необходимо отметить такие особенности решения задачи идентификации параметров макромоделей тепловых сетей на основе данных эксплуатации, как наличие ошибок в измерении значений расхода, температуры и давления теплоносителя на источниках и у потребителей и неполнота информации о характеристиках, содержащихся в данных эксплуатации. Поэтому решение задачи идентификации параметров макромоделей тепловых сетей должно включать в себя регуляризацию на основе регуляризующих наборов данных, которые являются дополнительными для восполнения недостающей информации в данных реальных наблюдений. В качестве регуляризующих наборов данных могут быть использованы расчетные значения сопротивлений участков SC по формуле (5.8) или экспертные оценки полученных в результате моделирования значений напоров HП у потребителей в рассматриваемых режимах. В результате для регуляризующих данных составляется целевая функция:
где n – число регуляризующих данных. Тогда результирующая целевая функция при решении задачи идентификации параметров макромоделей тепловых сетей будет иметь вид:
где a – вес регуляризующих данных J 2, который выбирается из условия корректности постановки задачи. При a = 0 задача решается только на экспериментальных данных; при a = 1 задача решается только на регуляризующих данных. При выборе значения коэффициента a необходимо задавать минимально возможное значение, при котором сохраняется корректность постановки задачи, т.е. выполнятся критерий J 2 с заданной точностью e. Таким образом, предлагаемая методика позволяет проводить идентификацию параметров математической макромодели тепловой сети по данным эксплуатации тепловых сетей. Применение на практике математической макромодели тепловой сети, описанной выше, в составе автоматизированной системы диспетчерского управления позволяет оперативно анализировать функционирование систем теплоснабжения в различных режимах и повысить эффективность и надежность процесса теплоснабжения.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.32.238 (0.008 с.) |

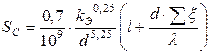 , мм×ч2/м6, (5.8)
, мм×ч2/м6, (5.8)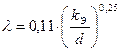 .
.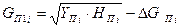 ,
, 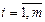 . (5.9)
. (5.9)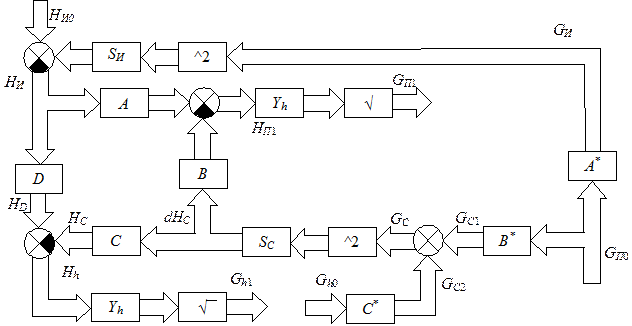
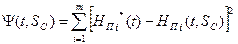 ,
,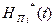 - измеренные в определенный момент времени t значения напоров теплоносителя на абонентских вводах потребителей тепла;
- измеренные в определенный момент времени t значения напоров теплоносителя на абонентских вводах потребителей тепла; 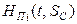 - рассчитанные значения напоров, соответствующие измеренным расходам теплоносителя на абонентских вводах потребителей G* при значениях сопротивлений участков сети SС.
- рассчитанные значения напоров, соответствующие измеренным расходам теплоносителя на абонентских вводах потребителей G* при значениях сопротивлений участков сети SС.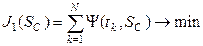 . (5.12)
. (5.12)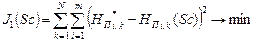 , (5.13)
, (5.13)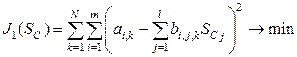 ,
,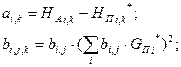
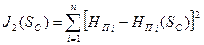 ,
,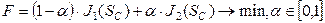 ,
,


