
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи оптимизация технологических объектовСодержание книги
Поиск на нашем сайте
Постановка задачи оптимизации Оптимизация характеристик систем заключается в максимизации или минимизации некоторого параметра системы. Систему, процессы в которой необходимо оптимизировать, назовем объектом управления. Состояние объекта описывается многомерной переменной х = (x(1),…, x(n)), определенной на множестве допустимых значений Х. Если величины х(i) могут изменяться непрерывно, то на них накладываются ограничения, имеющие вид алгебраических уравнений или неравенств:
Таким образом, общую постановку задачи оптимизации можно задать в следующем виде: Требуется найти такой вектор состояния объекта управления x = (x(1),…, x(n))T из допустимой области X, который приводит к минимуму целевую функцию g(x), то есть такой вектор x* Существуют методы решения задачи оптимизации, называемые математическим программированием. Эти методы дают возможность найти значения переменных x(1),…, x(n), удовлетворяющих ограничениям типа (3.20) и обращающих в минимум целевую функцию g(x). К таким методам относятся задачи линейного и нелинейного программирования. Задача линейного программирования соответствует случаю, когда ограничения и целевая функция являются линейными зависимостями от х. В задаче нелинейного программирования ограничения и целевая функция могут нелинейно зависеть от х.
Применение стандартных средств Excel для решения задачи оптимизации Для решения задач, требующих применения математического аппарата линейного и нелинейного программирования и методов исследования операций, используется надстройка «Поиск решения» в Excel, которая вызывается следующими действиями: Сервис (на панели задач) -> Поиск решения:
Рис. 3.25
Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут ссылаться на другие влияющие ячейки.
Целевая ячейка представляет собой цель. Нам нужно получить либо минимальное, либо максимальное значение целевой ячейки. В некоторых ситуациях может быть несколько целевых ячеек. Положим, в ячейке, которую мы назначаем целевой, содержится функция g(x1,x2) = 3x1+2x2, и нам необходимо найти ее максимальное значение. Формула в целевой ячейке содержит ссылки на изменяемые ячейки – это ячейки электронной таблицы, которые можно изменять или настраивать, чтобы оптимизировать целевую ячейку. В нашем случае в изменяемых ячейках будут содержаться переменные x1, x2. Ограничения устанавливаются для изменяемых ячеек. В большинстве моделей поиска решений существует неявное ограничение, что все изменяемые ячейки должны быть неотрицательными. В модели поиска решений использование каких-либо ограничений необязательно. Допустим, в качестве ограничений мы укажем x1 Любая спецификация изменяемых ячеек, удовлетворяющая ограничениям модели, называется подходящим решением. По существу, «Поиск решения» находит все подходящие решения, с «наилучшим значением» целевой ячейки (максимальным для оптимизации по максимуму, минимальным для оптимизации по минимуму). Такое решение называется оптимальным решением. Для некоторых моделей поиска решения оптимального решения не существует, а для некоторых существует только единственное решение. Для других моделей поиска решения существует несколько (фактически бесконечное количество) оптимальных решений. Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки. В нашем случае после выполнения процедуры поиска решений получаем, что максимальным значением целевой ячейки является значение 53 при x1 = 11, x2 = 10.
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.24.177 (0.01 с.) |

 (3.20)
(3.20) X, для которого выполняются условия g(x*)
X, для которого выполняются условия g(x*) 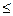 g(x)
g(x)  x
x 



