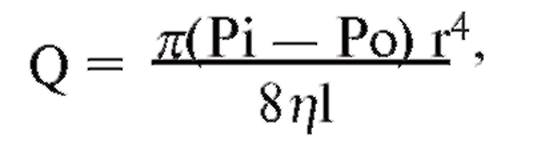Соотношение между площадью поперечного сечения, давлением и средней линейной скоростью кровотока в различных отделах сердечно-сосудистой системы

Скорость кровотока. Линейная скорость

Перед описанием изменения кровотока в разных сосудах необходимо ввести термины скорость (velocity) и объемная скорость (flow) кровотока и определить их различия. Скорость, которую иногда называют линейной скоростью, является скоростью перемещения жидкости в единицу времени и выражается в единицах расстояния, пройденного кровью, за единицу времени (например, см/с). Объемная скорость кровотока, которую часто называют объемным кровотоком, выражается в единицах объема крови, пройденного за единицу времени (например, см³/с). Для трубки с переменными размерами поперечного сечения взаимосвязь линейной скорости (v), объемной скорости (Q) и площади поперечного сечения (А) выражается уравнением:

Взаимосвязь между скоростью, объемной скоростью и площадью поперечного сечения трубки изображена на рис. 6-59 А. Согласно принципу сохранения массы, поток несжимаемой жидкости через последовательно расположенные жесткие трубки с разными поперечными сечениями должен оставаться постоянным. При заданном потоке изменения линейной скорости жидкости обратны изменениям площади поперечного сечения трубки. Таким образом, когда жидкость в трубке поступает из сции а в сцию b, где площадь поперечного сечения в пять раз больше, линейная скорость жидкости уменьшается до ¹/₅ своего предыдущего значения, так как площадь поперечного сечения сции b в 5 раз больше площади поперечного сечения сции а (рис. 6-59 А). Напротив, когда жидкость поступает из секции b в сцию с, площадь поперечного сечения которой равно ¹/₁₀ площади поперечного сечения сции b, скорость потока жидкости 10-кратно возрастает.

Линейная скорость жидкости в любой точке гидравлической системы зависит не только от площади поперечного сечения, но также и от объемной скорости кровотока Q. Объемная скорость, в свою очередь, зависит от градиента давления, особенностей жидкости и общих размеров

гидравлической системы, что рассматривается в следующем разделе. Впрочем при любой заданной объемной скорости, отношение линейной скорости жидкости, проходящей через одну площадь поперечного сечения, к линейной скорости жидкости, проходящей через вторую площадь поперечного сечения, зависит только от обратной пропорции этих площадей, т.е.:

Это правило относится и к системам, состоящим из одной большой трубки, и к системам, состоящим из нескольких трубок меньшего размера, расположенных параллельно.

Как показано на рис. 6-59 Б, линейная скорость кровотока прогрессивно уменьшается по мере того, как кровь проходит по аорте, затем по артериям все меньшего диаметра и по артериолам. Наконец, в капиллярах скорость падает до своего минимального значения. Так как кровь затем проходит по венулам и продолжает двигаться по направлению к центру, к полым венам, скорость снова прогрессивно возрастает. Соответствующие скорости кровотока в разных отделах системы кровообращения связаны только с соответствующими площадями поперечных сечений. Таким образом, каждая точка на графике площади поперечного сечения обратно пропорциональна соответствующей точке на кривой линейной скорости кровотока (рис. 6-59 Б).

От каждой артериолы отходит много капилляров. Общая площадь поперечного сечения капиллярного русла весьма значительна, несмотря на то, что площадь поперечного сечения отдельного капилляра меньше площади отдельной артериолы. В результате скорость кровотока в капиллярах значительно снижается, подобно тому, как замедляется течение воды (рис. 6-59 Б) на широких участ-ках реки. Так как капилляры состоят из коротких трубок со стенками толщиной всего в одну клетку и скорость кровотока в них низкая, в капиллярах создаются идеальные условия для обмена веществ между кровью и тканями путем диффузии.

Площадь поперечного сечения полых вен больше, чем у аорты, поэтому скорость движения крови в полых венах ниже, чем в аорте (рис. 6-59 Б).

Рис. 6-59. Линейная скорость кровотока.

А - при движении жидкости в гидравлической системе с переменной площадью поперечного сечения, а - изменения линейной скорости, v - обратны изменениям площади поперечного сечения. Q - объемная скорость. Б - скорость движения крови и площадь поперечного сечения кровеносных сосудов в различных отделах сосудистой системы. Важными особенностями здесь являются: обратная зависимость между скоростью движения крови и площадью поперечного сечения сосудов, наибольшее падение давления в малых артериях и артериолах и максимальная площадь поперечного сечения у капилляров при минимальной скорости движения крови в капиллярах

Взаимосвязь линейной скорости кровотока и величины давления

В определенной части гидравлической системы, где общая энергия остается фактически постоянной, изменения линейной скорости могут сопровождаться ощутимыми изменениями динамической составляющей измеренного давления. Рассмотрим три сции (А, В и С) гидравлической системы, изображенной на рис. 6-60 А. Шесть зондов для измерения давления, или трубок Пито, введены в различные точки этой гидравлической системы. Отверстия трех из этих трубок Пито (2, 4 и 6) направлены по касательной к направлению течения жидкости в гидравлической системе, таким образом они измеряют боковое, или статичное, давление внутри сций разного диаметра этой гидравлической системы. Отверстия остальных трех трубок Пито (1, 3 и 5) направлены навстречу течению жидкости в гидравлической системе. Эти трубки Пито измеряют общее давление, которое складывается из бокового давления и динамической составляющей, величина которой зависит от кинетической энергии текущей жидкости. Эту динамическую составляющую (Pd) общего давления можно вычислить с помощью следующего уравнения:

где ρ - это плотность жидкости, а v - ее линейная скорость. Если трубки Пито (1, 3 и 5) в сциях А, В и С изучаемой гидравлической системы будут установлены на одинаковом среднем уровне (т.е. находятся на одном гидростатическом уровне), то соответствующие общие давления Р₁, Р₃ и Р₅, будут равными, при условии, что потерей энергии из-за вязкости жидкости в этих сциях можно пренебречь (другими словами, жидкость, которую мы здесь рассматриваем, есть «идеальная жидкость»). Однако вследствие разницы в площади поперечного сечения вдоль этой гидравлической системы, соответствующие изменения линейной скорости жидкости изменяют динамическую составляющую, как показывает приведенное выше уравнение.

Пусть в сциях гидравлической системы А и С ρ будет равно 1 г/см³ и пусть v будет равна 100 см/с. вспомним также, что 1 мм рт.ст. равен 1330 дин/см². Тогда:

Пусть в узкой сции трубки, В, линейная скорость жидкости будет в 2 раза больше линейной скорости в сциях А и С. Поэтому в узкой сции гидравлической системы

Следовательно, в широких сциях гидравлической системы (А и С) значения бокового давления (Р₂ и будут лишь на 3,8 мм рт.ст. ниже соответствующих значений общего давления (Р₁ и Р₅), тогда как в узкой сции гидравлической системы (В) боковое давление (Р₄) будет ниже общего давления (Р₃) на 15 мм рт.ст.

На основании этих вычислений мы можем сделать два обобщения. Первое: при уменьшении линейной скорости доля динамической составляющей (величина которой, как вы помните, зависит от кинетической энергии текущей жидкости) в общем давлении тоже уменьшается. Второе: в узких участках гидравлической системы динамическая составляющая значительно увеличивается, потому что линейная скорость потока жидкости связана с освобождением кинетической энергии.

Записи давления, представленные на рис. 6-60 В, были получены с помощью двух датчиков давления, вставленных в левый желудочек сердца, у пациента со стенозом устья аорты. Когда оба датчика находились глубоко в полости левого желудочка (рис. 6-60 В1), оба они регистрировали одинаковое давление. Однако когда ближайший датчик был помещен в устье аорты в области клапанов (рис. 6-60 В2), боковое давление, зарегистрированное во время сердечного выброса, оказалось значительно ниже давления, зарегистрированного датчиком, находившимся в полости желудочка. Причина этой разницы давлений почти целиком заключается в том, что в суженном устье аорты линейная скорость кровотока гораздо выше, чем в полости желудочка.

Рис. 6-60. Связь между линейной скоростью кровотока и боковым давлением.

А - в узкой сции В гидравлической системы линейная скорость, v, а следовательно, и динамическая составляющая давления, ρν ²/2, больше, чем в широких сциях этой же гидравлической системы, А и С. Если общая энергия является фактически постоянной на протяжении всей гидравлической системы (т.е. если потерей энергии из-за вязкости жидкости можно пренебречь), то значения общего давления (Р₁, Р₃ и Р₅) не будут сколько-нибудь ощутимо отличаться друг от друга, но боковое давление, Р₄, в узкой сции будет меньше бокового давления (Р₂ и Р₆) в широких сциях трубки. Б - линейная скорость кровотока в восходящем и нисходящем участках аорты собаки. В - показатели давления (Р), записанные двумя датчиками у пациента со стенозом аорты. В1 - оба датчика находились в левом желудочке (ЛЖ-ЛЖ); В2 - один датчик в левом желудочке, а другой в устье аорты в области клапанов (ЛЖ-УА); В3 - один датчик находился в левом желудочке, а другой - в восходящем участке аорты (ЛЖ-ВА)

Ламинарный и турбулентный потоки жидкости в сосуде

Введем ряд понятий. Термин «равномерный поток - steady flow» означает отсутствие изменений в потоке жидкости на протяжении времени (т.е. не пульсирующий поток жидкости). Термин ламинарный поток - laminar flow является таким типом движения, когда жидкость движется в виде последовательности отдельных слоев, причем каждый слой движется со своей скоростью, отличной от скорости соседних слоев (рис. 6-61 А). При ламинарном течении в трубке жидкость состоит из последовательности бесконечно малых тонких концентрических слоев, скользящих один относительно другого.

По мере движения жидкости в трубке тонкий слой жидкости, соприкасающийся со стенками трубки, прилипает к стенкам и, таким образом, остается неподвижным. Слой жидкости, находящийся ближе к центру непосредственно после этого тонкого внешнего слоя, должен продвигаться мимо неподвижного слоя, и поэтому этот слой движется медленно, но с умеренной скоростью. По этому же принципу следующий слой, расположенный ближе к центру, движется быстрее; продольный профиль скорости здесь имеет форму параболоида. Частицы жидкости, находящиеся в любом слое, остаются в этом же слое, пока жидкость движется в трубке в продольном направлении. Скорость в осевой части потока максимальна и в 2 раза выше средней скорости потока на всей площади поперечного сечения трубки.

Беспорядочное движение частиц жидкости может привести к развитию неравномерного течения жидкости в трубке; такое течение называется турбулентным. При таких условиях частицы

жидкости не остаются в определенном слое, а происходит их быстрое перемешивание в радиальном направлении (рис. 6-61 Б). Для продвижения заданного потока жидкости по одной и той же трубке требуется значительно большее давление при турбулентном потоке, чем при ламинарном. При турбулентном течении падение давления примерно пропорционально квадрату скорости потока, тогда как при ламинарном течении падение давления пропорционально скорости потока в первой степени. Таким образом, чтобы создать заданный поток жидкости, насос, такой, как сердце, должен проделать значительно большую работу при возникновении турбулентного течения.

Турбулентным или ламинарным будет течение жидкости в трубке при заданных условиях, можно предсказать с помощью безразмерной величины, называемой числом Рейнольдса, N_R. Эта величина представляет собой отношение сил инерции к силе внутреннего трения (вязкости). Для жидкости, текущей в цилиндрической трубке,

где ρ - плотность жидкости, D - диаметр трубки, v - средняя скорость и η - вязкость. При N_R менее 2000 течение обычно бывает ламинарным; при N_R больше 3000 течение будет турбулентным; при N_R от 2000 до 3000 течение будет переходным между ламинарным и турбулентным. Уравнение показывает, что высокая плотность жидкости, большие диаметры трубок, высокая линейная скорость потока и низкая вязкость жидкости предрасполагают к возникновению турбулентности. Кроме перечисленных причин, турбулентность может быть вызвана резким изменением размеров трубки или неровностями стенок трубки.

Рис. 6-61. Ламинарный и турбулентный потоки жидкости в сосуде.

А - при ламинарном течении все мельчайшие частицы жидкости движутся в потоках, параллельных оси трубки; движения жидкости в радиальном направлении или по окружности не происходит. Пристеночный слой жидкости неподвижен; центральный поток жидкости в трубке имеет максимальную скорость. Б - в турбулентном потоке мельчайшие частицы жидкости беспорядочно движутся в центральном, радиальном и круговом направлениях. Часто наблюдаются вихревые движения и переход через среднюю линию

Объемная скорость течения жидкости зависит от давления

Гемодинамика подчиняется основным главным законам гидродинамики, а основной закон, которому подчиняется движение жидкостей в цилиндрических трубках, был выведен эмпирическим путем Пуазейлем.

Закон Пуазейля применим только к равномерному ламинарному потоку ньютоновских жидкостей в цилиндрических трубках. (Подробнее термин «ньютоновские жидкости» будет объяснен ниже).

Говоря упрощенно, закон Пуазейля описывает движение жидкостей в цилиндрических трубках, используя такие характеристики, как объемная скорость, давление, размеры трубки и вязкость жидкости, находящейся в трубке. На следующих страницах эти термины рассмотрены подробно и затем соотнесены друг с другом для выведения закона Пуазейля.

Давление является одной из главных причин, определяющих скорость потока. Давление Р, измеряемое в динах/см², на расстоянии h см ниже поверхности жидкости равно:

где ρ - это плотность жидкости, измеряемая в г/ см³, аg - это ускорение силы тяжести в см/с². Однако для удобства давление часто выражают просто как высоту столба жидкости (h) над произвольной исходной точкой.

Рассмотрим трубку, соединяющую резервуары R₁ и R₂ на рис. 6-62 А. Резервуар R₁ заполнен

жидкостью на высоту h₁, а резервуар R₂ - пуст. Поэтому давление жидкости, вытекающей в резервуар R₂ из соединяющей эти резервуары трубки, обозначенное как Р₀, равно атмосферному давлению, которое следует принять за нулевой, или исходный, уровень. Давление жидкости, втекающей в трубку из резервуара R₁, обозначенное как Р_i, будет равно сумме исходного уровня и высоты столба жидкости h₁ в резервуаре R₁. При этом пусть объемная скорость жидкости (Q), протекающей через трубку будет равна 5 мл/с.

На рис. 6-62 Б, резервуар R₁ наполнен до высоты h₂, которая в 2 раза больше, чем h₁, а резервуар R₂ снова пуст. Объемная скорость жидкости в части В рисунка в два раза больше, чем в части А (т.е. 10 мл/с). Следовательно, когда давление жидкости, вытекающей в резервуар R₂ из соединяющей эти резервуары трубки, обозначенное как (Р₀) равно нулю, объемная скорость прямо пропорциональна давлению жидкости Р_i втекающей в трубку из резервуара R₁. Если сейчас дать резервуару R₂ заполниться на высоту h₁, а уровень жидкости в R₁ поддерживать на высоте h₂ (как на рис. 6-62 В), то объемная скорость снова будет 5 мл/с. Следовательно, объемная скорость жидкости прямо пропорциональна разнице между давлением втекающей в трубку жидкости и давлением вытекающей из трубки жидкости:

Если уровень жидкости в R₂ достигнет такой же высоты, как в R₁, движение жидкости по трубке прекратится (рис. 6-62 Г).

Рис. 6-62. Объемная скорость жидкости, Q, в трубке, соединяющей два резервуара, R₁ и R₂, пропорциональна разнице между давлением Р_i в том конце трубки, по которому жидкость втекает в трубку из резервуара R₁, и давлением Р₀ в том конце трубки, из которой жидкость вытекает из трубки в резервуар R₂.

А - когда R₂ пуст, жидкость течет из R₁ в R₂ со скоростью, пропорциональной давлению в Б - когда уровень жидкости в R₁поднимается в два раза, объемная скорость жидкости пропорционально увеличивается. В - объемная скорость жидкости, текущей из R₁ в R₂, пропорциональна разнице давлений в резервуарах R₁ и R₂. Г - когда давление в R₂ повышается и становится равным давлению в R₁, движение жидкости в соединяющей трубке прекращается

Зависимость объемной скорости от размеров трубки

Рассмотрим, как на объемную скорость влияют размеры трубки. При любой заданной разнице давлений в двух концах трубки объемная скорость зависит от размеров трубки. Рассмотрим трубку, соединенную с резервуаром на рис. 6-63 А. При длине трубки l₁ и радиусе r₁объемная скорость Q₁ равна 10 мл/с. Трубка, соединенная с резервуаром на рис. 6-63 Б, имеет такой же радиус, но вдвое длиннее трубки, представленной в части А рисунка. При таких условиях объемная скорость Q₂ будет равна 5 мл/с, или лишь ¹/₂ объемной скорости Q₁. Другими словами, объемная скорость жидкости обратно пропорциональна длине трубки:

Длина трубки, соединенной с резервуаром на рис. 6-63 В равна l₁, но ее радиус, r₃, в 2 раза больше r₁. В этих условиях наблюдается увеличение объемной скорости Q₃, до 160 мл/с, что в 16 раз больше Q₁. Точные измерения, сделанные Пуазейлем, позволили установить, что объемная скорость жидкости прямо пропорциональна радиусу трубки в четвертой степени:

Таким образом, так как r₃ = 2r₁, в вышеприведенном примере Q3 будет пропорциональна (2r₁)⁴, или 16r₁⁴; поэтому Q3 будет равна 16Q₁.

На рис. 6-63 Г продемонстрировано влияние вязкости жидкости на объемную скорость. Детально этот вопрос обсуждается на следующем рисунке.

Рис. 6-63. Объемная скорость жидкости в трубке, Q, обратно пропорциональна длине трубки, l, и вязкости жидкости, η, и прямо пропорциональна радиусу трубки, r, в четвертой степени.

А - исходное условие: при заданных величинах давления, длины, радиуса и вязкости пусть объемная скорость, Q₁, будет равна 10 мл/с. Б - если длину трубки увеличить вдвое, объемная скорость уменьшится на 50%. В - если радиус трубки увеличить вдвое, объемная скорость увеличивается в 16 раз. Г - если вязкость жидкости увеличивается в 2 раза, объемная скорость уменьшается на 50%

Вязкость крови

При заданной разнице давлений и при заданных размерах цилиндрической трубки объемная скорость жидкости зависит и от природы самой жидкости. Свойство жидкостей, влияющее на скорость их движения, называется вязкостью η, которую Ньютон определил как отношение напряжения сдвига (shear stress) к скорости сдвига (shear rate).

Смысл этих терминов можно яснее всего понять, рассматривая поток однородной жидкости между параллельными пластинами. На рис. 6-64 нижняя пластина (дно большого бассейна) неподвижна, а верхняя пластина движется по поверхности жидкости. Напряжение сдвига τ, определяется как отношение F:A, где F - сила, приложенная к верхней пластине в направлении ее движения по поверхности жидкости, а А - это площадь верхней пластины, соприкасающаяся с жидкостью. Скорость сдвига равна du/dy, где u - это линейная скорость мельчайшей частицы жидкости в направлении, параллельном движению верхней пластины, а у - это расстояние от этой частицы текущей жидкости до нижней, неподвижной пластины.

Для пластины, которая движется с постоянной скоростью U по поверхности однородной жидкости, тип скорости потока жидкости будет линейным. Слой жидкости, соприкасающийся с верхней пластиной, будет прилипать к ней и поэтому двигаться с той же самой скоростью U, что и пластина. Каждая мельчайшая частица жидкости между пластинами будет двигаться со скоростью u, пропорциональной расстоянию у, на которое частица отстоит от нижней пластины. Поэтому скорость сдвига будет равна U/Y, где Y - это расстояние

между двумя пластинами. Так как вязкость η определяется как отношение напряжения сдвига τ, к скорости сдвига, du/dy, то в примере, показанном на рис. 6-64,

Таким образом, единица измерения вязкости - это дин/см², деленный на (см/с)/см, или дин•с/см². В честь Пуазейля 1 дин•с/см² был назван Пуазом. Вязкость воды при 20 °С составляет примерно 0,01 пуаза, или 1 сантипуаз. У ряда неоднородных жидкостей, в особенности у суспензий, таких, как кровь, отношение напряжения сдвига к скорости сдвига не является постоянным, т.е. жидкость не обладает постоянной вязкостью. Такие жидкости называют неньютоновскими. Что касается движения ньютоновских жидкостей в цилиндрических трубках, то их объемная скорость изменяется обратно пропорционально их вязкости.

Возвращаясь к примеру с движением жидкости из резервуара: если вязкость жидкости в резервуаре увеличится вдвое, объемная скорость уменьшится в 2 раза (5 мл/с вместо 10 мл/с).

Подытожим: при равномерном ламинарном течении ньютоновской жидкости в цилиндрической трубке объемная скорость жидкости, Q, изменяется прямо пропорционально разнице давлений, P_i - P_o, и радиусу трубки, r, в четвертой степени, и обратно пропорционально длине трубки, l, и вязкости жидкости, η. Полная формула закона Пуазейля выглядит следующим образом:

где π/8 - коэффициент пропорциональности.

Рис. 6-64. Для ньютоновской жидкости вязкость η определяется как отношение напряжения сдвига τ к скорости сдвига du/dy. Для пластинки, плывущей по поверхности жидкости и имеющей площадь соприкосновения с поверхностью жидкости А, τ равно отношению силы F, приложенной в направлении движения, к площади соприкосновения А; du/dy равно отношению линейной скорости пластинки U к глубине жидкости Y

Сопротивление при последовательном и параллельном расположениях сосудов

Применение закона Пуазейля показывает, что сопротивление потоку жидкости зависит только от размеров трубки и характеристик жидкости:

Так как изменения сопротивления обратно пропорциональны радиусу трубки в четвертой степени, основным фактором, определяющим сопротивление кровотоку в любом отдельном сосуде системы кровообращения, является диаметр сосуда.

Сопротивление последовательно расположенных сосудов продемонстрировано на рис. 6-65 А. В этой системе три гидравлических сопротивления, R₁, R₂ и R₃, расположены последовательно. Общее падение давления в системе, т.е. разница между давлением притекающей жидкости, Pi, и давлением вытекающей жидкости, P₀, представляет собой сумму значений разницы давлений в каждом отдельном сопротивлении (уравнение а). При статичном состоянии системы объемная скорость жидкости, Q, в любом заданном поперечном сечении должна быть равна объемной скорости в любом другом поперечном сечении. При делении каждого компонента уравнения а на Q (уравнение b) из определения сопротивления становится очевидным, что при последовательно расположенных сопротивлениях общее сопротивление всей системы, R_t, равно сумме сопротивлений всех отдельных элементов, т.е.

Сопротивление параллельно расположенных сосудов продемонстрировано на рис. 6-65 Б. При параллельном расположении сопротивлений давление притекающей жидкости и давление вытекающей жидкости одинаковы у всех трубок. При статичном состоянии системы общая объемная скорость, Q_t, равна сумме объемных скоростей

в отдельных параллельно расположенных элементах системы (уравнение а). Так как градиент давления (Р_i - Р₀) один и тот же во всех параллельно расположенных элементах, каждую составляющую уравнения а можно разделить на этот градиент для получения уравнения b. Из определения сопротивления можно вывести уравнение с, которое устанавливает, что при параллельном расположении сосудов обратная величина общего сопротивления, R_v, равна сумме обратных величин отдельных сопротивлений, т.е.:

Более простой способ вывести это отношение - использовать термин «гидравлическая проводимость», которую можно определить как величину, обратную сопротивлению.

Сопротивление кровотоку малых артерий и артериол (что демонстрируется падением давления от артериол до капиллярных концов этих сосудов) значительно выше сопротивления кровотоку других сосудов артериальной системы, таких как крупные артерии, несмотря на то, что общая площадь поперечного сечения малых артериальных сосудов превышает площадь поперечного сечения крупных артерий (рис. 6-65 В).

Рассмотрение простых моделей систем, состоящих из параллельных трубок, поможет понять этот явный парадокс. На рис. 6-65 В сопротивление потоку жидкости в одной широкой трубке, имеющей площадь поперечного сечения А_w, сравнивается с сопротивлением потоку жидкости в четырех более узких трубках, расположенных параллельно, с площадью поперечного сечения каждой трубки A_n. Общая площадь поперечного сечения четырех параллельных узких трубок равна площади поперечного сечения широкой трубки. Анализ показывает, что общее сопротивление R_t четырех узких параллельных трубок в 4 раза больше сопротивления одной широкой трубки R_wпри одинаковой общей площади поперечного сечения.

Рис. 6-65. Сопротивление кровотоку.

А - при последовательном расположении общее сопротивление, Rt, равно сумме сопротивлений отдельных элементов (R₁, R₂и R₃). P - давление, Q - объемная скорость потока. Б - при параллельном расположении величина, обратная общему сопротивлению, Rt, равна сумме обратных величин сопротивлений отдельных элементов. В - когда четыре узкие трубки, каждая площадью поперечного сечения А_n, расположены параллельно, их общая площадь поперечного сечения равна площади поперечного сечения широкой трубки, A_w, т.е. A_w = 4А_n. Хотя общие площади поперечного сечения равны, общее сопротивление потоку жидкости в параллельных узких трубках, R_t, в 4 раза выше сопротивления потоку жидкости в одной широкой трубке, R_w. R_n - сопротивление одной узкой трубки; k - коэффициент пропорциональности

Реология крови

Вязкость ньютоновской жидкости, такой, как вода, можно определить с помощью измерения равномерного ламинарного течения жидкости при заданном градиенте давления в цилиндрической трубке известной длины и радиуса. Вязкость затем вычисляется подстановкой этих величин в уравнение Пуазейля. Вязкость определенной ньютоновской жидкости при определенной температуре будет постоянной при любых размерах трубки и объемной скорости потока. Однако вязкость неньютоновской жидкости, вычисленная с помощью уравнения Пуазейля, может значительно изменяться в зависимости от размеров трубки и объемной скорости потока. Поэтому при рассмотрении реологических свойств суспензии, такой, как кровь, термин «вязкость» имеет не одно значение. Термины аномальная вязкость и структурная вязкость (apparent viscosity) часто применяют для обозначения вязкости крови, в условиях, в которых проводились измерения.

С точки зрения реологии кровь представляет собой суспензию форменных элементов, главным образом, эритроцитов, в относительно однородной жидкости - плазме крови. Так как кровь - это суспензия, то структурная вязкость крови меняется в зависимости от гематокритного числа (отношения объема красных кровяных клеток к объему цельной крови). Вязкость плазмы в 1,2-1,3 выше вязкости воды. У крови с нормальным числом гематокрита - 45% - структурная вязкость в 2,4 раза выше, чем у плазмы.

При любом заданном гематокритном числе структурная вязкость крови зависит от размеров трубки, используемой при измерении вязкости. Структурная вязкость крови прогрессивно уменьшается, когда диаметр трубки становится меньше 0,3 мм. Диаметр артериол - кровеносных сосудов, имеющих самое высокое сопротивление, -

значительно меньше этого критического значения. Это и является причиной уменьшения сопротивления кровотоку в кровеносных сосудах с наибольшим сопротивлением. Влияние диаметра трубки на структурную вязкость крови частично объясняется действительным изменением состава крови при ее движении через маленькие трубки. Состав изменяется, потому что красные кровяные клетки собираются в быстром центральном потоке, тогда как плазма чаще движется в более медленных боковых слоях.

К чему приводит разница скорости движения красных кровяных клеток и скорости плазмы, можно понять на примере следующей аналогии: рассмотрим движение транспортного потока по тоннелю длиной 3 мили. Пусть автомобили движутся по одной линии со скоростью 60 миль в час, а грузовики по другой линии со скоростью 20 миль в час, как показано на рис. 6-66. Если каждую минуту одна автомашина и один грузовик въезжают в тоннель и начинают свое движение в тоннеле, тогда, за исключением нескольких первых минут движения транспорта, каждую минуту одна автомашина и один грузовик будут подъезжать к другому концу тоннеля. Если посчитать фактическое количество автомобилей и грузовиков в тоннеле в любой момент, то окажется, что медленно движущихся грузовиков в тоннеле в 3 раза больше, чем быстро проезжающих машин.

Так как центральные слои кровотока содержат больше красных кровяных клеток и движутся с большей скоростью, то красные кровяные клетки обычно проделывают весь путь по трубке быстрее, чем плазма. Поэтому в вышеприведенной аналогии красные кровяные клетки соответствуют быстро проезжающим автомобилям, а плазма - медленно движущимся грузовикам. Измерение времени прохождения крови через различные органы показало, что красные кровяные клетки движутся быстрее плазмы.

Рис. 6-66. Модель, демонстрирующая разницу скорости движения красных кровяных клеток и скорости плазмы.

Когда скорость автомобиля в 3 раза больше скорости грузовика, отношение количества автомобилей к количеству грузовиков на мосту будет 1:3 после 9 мин движения, даже если каждую минуту по одной машине каждого типа въезжает в тоннель и выезжает из тоннеля

Гидравлический фильтр артериальной системы

Основной функцией артериальной системы большого круга кровообращения и артериальной системы легких является доставка крови в капилляры сосудистого русла всего организма. Артериолы - кровеносные сосуды, которыми заканчивается ветвление артерий. Артериолы являются сосудами высокого сопротивления, которые регулируют распределение кровотока к различным капиллярам. В силу своей эластичности аорта, легочная артерия и их основные ветви формируют систему сосудов, способных вмещать значительные объемы крови. Два этих свойства артериальной системы, ее эластичность и высокое сопротивление артериол, делают артериальную систему организма схожей с жидкостной системой, называемой гидравлическим фильтром, который способен смягчать колебания кровотока (жидкости). Таким образом, артериальная система организма представляет собой гидравлический фильтр. Этот фильтр является аналогом RC-фильтров (сопротивление-емкость) в электрических цепях.

Главное назначение артериальной системы как гидравлического фильтра состоит в том, что она преобразует прерывистый (пульсирующий) выброс из сердца в непрерывный кровоток через капилляры. Эта важная функция магистральных эластичных артерий вызывает ассоциацию с воздушными (компрессорными) камерами старинных ручных пожарных насосов. Такая камера содержала значительный объем сжатого воздуха. Сжатие воздуха, который оставался над уровнем

воды в воздушной камере, преобразовывало поступающую внутрь прерывистую струю воды из пожарной бочки в непрерывный поток на выходе из брандспойта пожарного шланга. Без такой воздушной камеры вода поступала бы рывками, делая борьбу с огнем, в лучшем случае, неэффективной, а в худшем - опасной.

Роль, которую играют крупные эластичные артерии в такой функции, как гидравлический фильтр, демонстрируется на рис. 6-67. В силу того, что сердце производит выброс крови прерывисто, весь объем сердечного выброса попадает в артериальную систему в период систолы. Систола обычно занимает всего лишь около ¹/₃ сердечного цикла. Однако, фактически, большая часть систолического объема в действительности перекачивается в момент короткой фазы быстрого изгнания, которая составляет около половины продолжительности систолы. Лишь незначительная часть энергии сердечного сокращения рассеивается, т.е. переходит в кинетическую энергию движущейся крови к капиллярам во время систолы. Большая часть энергии сохраняется - переходит в потенциальную энергию сосудистой стенки за счет ее растяжения кровью, поступившей в аорту при систоле (рис. 6-67 А и Б). Во время диастолы эластичная отдача (т.е. стремление эластичных артериальных стенок вернуться к исходному состоянию) превращает эту потенциальную энергию в кинетическую энергию потока крови, движущегося к капиллярам. Если бы артериальные стенки были жесткими, то кровоток к капиллярам во время диастолы прекращался бы (рис. 6-67 В и Г).

Рис. 6-67. При нормальной эластичности артерий кровь проходит через капилляры в течение всего сердечного цикла. Если артерии ригидны, то кровь проходит через капилляры во время систолы, а во время диастолы кровоток прекращается

Функция гидравлического фильтра

Гидравлический фильтр уменьшает рабочую нагрузку сердца. Для перекачки имеющегося пульсирующего кровотока требуется больше усилий, чем для равномерного. Чем более эффективно работает гидравлический фильтр, тем меньше усилий требуется. Проиллюстрир