
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Філософія, логіка та інші науки про сутність мислення.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
НАВЧАЛЬНИЙ ПЛАН КУРСУ ЗАГАЛЬНОЇ ЛОГІКИ
3. ОСНОВНІ ТЕОРЕТИЧНІ ПОЛОЖЕННЯ КУРСУ Тема 1. Предмет, структура та завдання Філософія, логіка та інші науки про сутність мислення. Розвиток логіки в Україні. 1. Історія логіки бере свій початок ще з Стародавньої Греції, Це вперше було зроблено Арістотелем (384—322 рр. до н. е.). Логіку він назвав аналітикою і дав детальний аналіз відкри- До логічних творів Арістотеля слід віднести «Аналітики І і II», «Топіку», «Категорії», «Про тлумачення», «Про софістичні спростування» та ін. Послідовники Арістотеля об’єднали ці твори під назвою «Органон» (знаряддя пізнання). Ряд важливих логічних проблем висвітлено у його головній філософській праці «Метафізика». Зокрема, саме тут викладено три основних закони формальної логіки: закон тотожності, закон несуперечності і закон виключеного третього. У часи Арістотеля і пізніше формальна логіка розроблялась представниками школи стоїків — Зеноном (бл. 336—254 рр. до н.е), Хризипом (бл. 281—208 рр. до н.е.), Сенекою (бл. 4—65 рр. н.е.) та ін. Якщо Арістотель у своїх творах головну увагу звертав на дослідження категоричного силогізму, то стоїки займались, головним чином, тими умовиводами, до яких складовими частинами входили умовні та розділові судження. Вони застосували ряд логічних категорій, які увійшли в сучасну символічну (математичну) логіку, — імплікацію[3], диз’юнкцію[4], кон’юнкцію[5] та ін. В епоху середньовіччя логіка Арістотеля була дуже популярною, але зазнала певної модифікації відповідно до основних настанов схоластичної догматики. Найвідомішими представниками цього періоду були французький філософ І. Росцелін (бл. 1050—1122), англійський філософ У. Оккам (1290—1300 — бл. 1349), шотландський філософ Д. Скотт (бл. 1265—1308), англійський філософ Ансельм Кентерберійський (1033—1109) та ін. Перші три з названих філософів були номіналістами[6]. Вони визнавали реально існуючими тільки одиничні тіла природи, а загальні поняття вважали лише назвами класів речей, подібних між собою. Ансельм Кентерберійський захищав позицію реалізму[7], сутність якої полягає в тому, що загальні поняття розглядались як надприродні самостійні сутності одиничних речей. Ці поняття реалісти вважали первинними, тобто такими, що існують реально, незалежно від одиничних речей. Проміжне між ними положення займали концептуалісти, або помірковані номіналісти[8]. До їх числа належав П. Абеляр (1079—1142). На відміну від номіналістів вони визнавали, що сутність загальних понять (універсалій) не зводиться до назв, імен, а має мислимий зміст, який, однак, не відображає ніяких сторін реально існуючих речей, що суперечить послідовно матеріальній теорії пізнання. У XIV—XVIІ ст. у зв’язку з потребами природознавства й промислового виробництва все гучніше стали лунати заклики створити нову логіку. Ця ідея була реалізована англійським філософом Ф.Беконом (1501—1626) у праці «Новий органон», яка повинна була, на думку автора, замінити арістотелівський «Органон». Силу своєї логіки він вбачав в індуктивному методі, що протиставлявся дедукції і силогістиці Арістотеля. Ф. Бекона називають творцем індуктивної логіки. Засновником сучасної логіки був Г. Лейбніц (1646—1716). Створена ним штучна мова була прототипом сучасних формалізованих мов логіки. Він створив загальний метод, за допомогою якого всі істини можна було звести до певного виду обчислення, сформулював закон достатньої підстави, оригінальне вчення про гіпотезу. У XIX ст. англійський філософ і логік Джон Стюарт Мілль (1806—1873) систематизував дослідження Бекона в галузі індуктивних методів причинних зв’язків явищ. З того часу питання індукції стали викладатись в курсах і навчальних посібниках з логіки окремим розділом. Інший аспект розвитку формальної логіки полягає у тому, що в обох її розділах — дедуктивному та індуктивному — почали застосовуватись методи логічних обчислень. Проникнення математичних методів в індуктивну логіку приводить до її модифікації в логіку імовірнісну, предметом якої стає вже вивчення методів оцінки істинності гіпотез. Перевагою математичної логіки є те, що завдяки символічному апарату, який там застосовується, стає можливим виражати точною математичною мовою досить складні судження, у котрих логічно пов’язано багато елементів. Однак це не означає, що всі проблеми формальної логіки можна розв’язати засобами символічної логіки. До речі, перша формалізована мова була побудована лише наприкінці ХІХ ст. Г. Фреге (1848—1925). Він увів поняття логічної функції й розрізнення властивостей речей і відношень. Проте засобів логічних обчислень виявилося недостатньо для дослідження сутності понять, співвідношення поняття і слова, природи індукції, методів аналогії тощо. У середині XIX ст. філософ Гегель ґрунтовно розробив діалектичну логіку, основні ідеї якої були викладені у його праці «Наука логіки». Марксизм, трансформувавши діалектичне вчення Гегеля на матеріалістичне підґрунтя, дійшов висновку, що діалектика, логіка і теорія пізнання діалектично тотожні між собою, у зв’язку з чим не потрібно трьох слів для означення одного й того самого поняття. Основні принципи діалектичної логіки: а) об’єктивність при розгляді предметів; б) всебічне охоплення предмета, в) розгляд предмета у його постійному русі, розвиткові; г) єдність історичного і логічного; д) єдність аналізу й синтезу; е) єдність форми і змісту; є) єдність кількісних і якісних характеристик; ж) єдність і боротьба протилежностей; з) заперечення заперечення. Сучасна формальна логіка є надзвичайно розгалуженою наукою і може бути розподілена на різні складові частини (розділи) (див. табл. 1 на стор. 19). Якщо за основу структурування логіки брати застосування математичного апарату (логічні числення), то тоді логіка поділяється на дві частини: 1) загальну (несимволічну) логіку; 2) символічну (математичну) логіку. У зв’язку з тим, що в даному курсі йдеться саме про загальну логіку, доцільно розглянути елементи її структури. По-перше, — це вчення про основні форми (елементи) мислення, без чого неможливе ні буденне, ні наукове мислення. До них відносять: поняття, судження, умовиводи. У цей розділ входить також вчення основних формально-логічних законів. По-друге, — це систематичні форми, без яких неможливе вивчення мислення, визначення систем поділу (класифікацій), доведення, логічні методи, пов’язані з аналізом даних досвіду, зокрема економіко-статистичних вимірів. Вираз «загальна логіка» у деяких випадках використовується для позначення теоретичної частини логіки, відмінної від прикладної. Крім того, існує «законсервована» культура логічного мислення, яка характеризує буддизм, школи ньяя, міманса (див. табл. 2 на стор. 19). 2. Логіка античних мислителів стала відомою в Київській Русі вже в XI ст. Це насамперед логічні уявлення про поняття Платона, про закони і форми мислення, силогізми Арістотеля. З другої половини ХV ст. з’являються переклади на староукраїнську мову логічних трактатів Арістотеля, Авіасафа, Аль-Газалі, М. Маймоніда, Й. Дамаскіна. У ХVІ ст. під впливом ідей Реформації на етнічних землях українців зростає мережа протестантських навчальних закладів, серед яких найбільш відома Раківська академія, де логіку і метафізику читали Х. Стегман та X. Остородт. Щоправда, в цей час спостерігалось також негативне ставлення до язичницьких любомудрів з боку І. Вишенського і Г. Кониського, М. Смотрицького, З. Копистенського. Але вже для членів вченого гуртка друкарні Києво-Печерської лаври логіка стає своєрідною «гімнастикою розуму», забезпечує розвиток абстрактного мислення і логічного виведення. Логіка стає обов’язковою дисципліною вивчення в Києво-Могилянській академії. Професор С. Яворський називав «лабіринт» Арістотеля логічною пасткою, де є логічні троянди з шипами. І. Гізель (1600—1683), професор, а згодом і ректор Києво-Могилянської академії, логічною істинністю називав узгоджуваність пізнання з річчю. У курсі логіки, прочитаному професором Ф. Прокоповичем (1677 чи 1681—1736), розглядалися такі традиційні для ХVІІІ ст. питання, як універсалії, визначення й характеристика найрізноманітніших відношень, дистинкцій, питання сигніфікації (позначення) й супозиції (заступання) термінів, істинності та хибності суджень, проблеми знання й віри, визначення ролі імісця логіки в системі наук. Засновник Харківського університету В. Каразін у листі до видавця альманаху «Молодик» І. Бецького від 2 березня 1842 р. охарактеризував Г. Сковороду таким чином: «Ми під чубом та в українській свитині мали свого Піфагора, Орігена і Лейбніца». Він намагався у світі чисел знайти вище значення в текстах Біблії, розвивав ідею про контрарність, бінарність усього сущого. Наприкінці ХVІІІ — початку XIX ст. логікою займався професор Львівського університету II. Д. Лодій (1764—1829). Він написав праці: «Логические наставления, руководствующие к познанию и различению истинного от ложного», «Наставления логики», «Теория общих правил», у яких значну увагу приділяв правилам аргументації і доведення. Наприкінці XIX — початку XX ст. логіка в Україні не була однорідна, а складалася з представників багатьох конкуруючих течій, шкіл та угруповань: одні (М. Н. Гротт та ін.) намагалися знайти вихід з критичного становища логічної науки у Засновником одеської логічної школи був І. В. Слєшинський (1854—1931), який виявив інтерес до математичної логіки та її історії. Він довів, що алгебра логіки є своєрідний переклад арістотелівської логіки на алгоритмічну мову, що необхідний перегляд математичних доведень під кутом зору їх повноти та заміни громіздких доведень новими, скороченими. До проблеми побудови алгебри без застосування закону виключеного третього звертався приват-доцент Новоросійського (Одеського) університету С. Й. Шатуновський (1859—1929). Його головні інтереси в галузі логіки зосереджувались на вивченні її законів, а також на обґрунтуванні фундаментальних математичних понять, обґрунтуванні математики, питанні про розв’язуваність чи нерозв’язуваність задач. Особливу увагу ученого привертали життя і діяльність П. Порецького (1846—1907), його теорія наслідків, несилогістичні міркування тощо. З одеської логіко-математичної школи вийшла також С. О. Яновська, праці якої присвячені філософсько-методологічним проблемам математики і математичної логіки, та А. І. Уйомов, праці якого присвячені проблемам аналогії, формального аналізу систем. На західних етнічних землях українців значний внесок у розвиток світової логіки зробила Львівсько-Варшавська школа. Заснов- У часи радянської влади в Україні формальну логіку тривалий час ігнорували і критикували як основу метафізичного методу, лише у другій половині 40-х років логіку в Радянській Україні частково «реабілітували»: стали читати курс традиційної логіки в деяких вузах Москви, Ленінграда, Києва, Новосибірська та інших міст. Сучасну ж логіку, зокрема логіку висловлювань і логіку предикатів вважали ворожими діалектичній логіці. Позитивні зрушення щодо сучасних напрямів логіки почалися в 60-ті ро- Таблиця 1 історичні етапи розвитку логіки
Таблиця 2 історичні етапи розвитку логіки
Питання для самостійної роботи 1. Вивчення формальної логіки як науки, її предмет, історія розвитку і загальне значення. 2. Що таке логічна форма? 3. Що таке суб’єкт і яким символом він позначається? 4. Що таке предикат, яким символом його позначають? 5. Які символи в логіці називають змінними і що вони означають? 6. Які символи називаються постійними і що вони означають? Який зміст постійного символу «деякі»? 7. Напишіть (назвіть) 5 тверджень відповідно до формули: всі S є Р. 8. Кожному з тверджень завдання 7 знайдіть логічно пов’язане з ним твердження за формулою: деякі S є Р. 9. Спробуйте з кожної пари тверджень, що ви дібрали, виконуючи завдання 7 та 8, зробити логічний висновок. 10. Заповніть конкретним змістом формулу: Всі М є Р. Всі S є М. Отже, S є Р. Тема 3. Поняття 1. Визначення, структура та основні методи творення понять. Таблиця основних видів понять
Відношення протилежності (контрарності) А — «прибуткове підприємство» В — «збиткове підприємство» А, В — протилежні (контрарні поняття), Відношення суперечності — це таке відношення між поняттями, коли одне з них містить ознаку, яку інше поняття її заперечує, не замінюючи заперечувану ознаку іншою. Поняття, що перебувають у такому відношенні, називаються суперечними, або контрадикторними.
А — «збитковий» не-А — «незбитковий» А, не-А — суперечні (контрадикторні) поняття
Визначення понять Визначенням, або дефініцією, називається логічна операція, що розкриває зміст поняття. Наприклад: «Холдингова компанія — це компанія, яка володіє контрольними пакетами акцій інших компаній». Поняття, зміст якого визначається, називається визначуваним поняттям (definiendum, скорочено — Dfd), а поняття, за допомогою якого розкривається зміст визначуваного поняття, визначаючим поняттям (definiens — Dfn). Якщо у визначенні розкривається тільки назва поняття, то воно називається номінальним (від лат. nomina — ім’я, назва). Якщо ж у визначенні розкриваються істотні ознаки предмета, то воно називається реальним. Види визначень і їх правила докладно висвітлювалися в підручниках з логіки. Найпоширенішим видом реальних визначень є визначення через найближчий рід і видову відмінність. Правила цього виду визначення студенти мають твердо знати і вміти використовувати їх на практиці. Поділ понять Логічна операція, що розкриває обсяг поняття, називається поділом поняття. Поняття, обсяг якого розкривається, називається діленим поняттям. Ознака, за якою здійснюється поділ, називається основою поділу, а поняття, одержані в результаті поділу, — членами поділу. Залежно від кількості членів поділу розрізняють поділ двочленний, тричленний і багаточленний. Серед двочленного поділу виділяють дихотомію (від грец. dicha — два і tome — поділ, розтин, тобто поділ на дві частини), що являє собою поділ обсягу діленого поняття С на два суперечних поняття — А і не-А: швидкий — нешвидкий, збитковий — незбитковий і т.п. Особливим видом поділу є класифікація. Від звичайного поділу класифікація відрізняється тим, що в ній поділ здійснюється за істотною, корінною ознакою, а члени поділу займають постійне і чітко фіксоване місце. Прикладом класифікації може служити періодична система хімічних елементів Менделєєва. Операція додавання понять. Це операція над обсягами понять, сутність якої полягає в об’єднанні двох або кількох множин, що становлять обсяги вихідних понять, в одну множину. Таблиця додавання понять
Операція множення понять. Це операція над поняттями, суть якої полягає в утворенні нового поняття, обсягом якого є елементи, спільні для вихідних понять. Таблиця множення понять
Віднімання понять. Це операція над поняттями, суть якої полягає в тому, що утворюється нове поняття, елементи якого не входять до поняття, яке віднімається. Таблиця віднімання понять
Операція доповнення обсягів понять. Це операція над поняттями, коли шляхом заперечення вихідного поняття А утворюють нове поняття А¢ (не-А), обсяг якого в сумі з обсягом поняття А становить цілісність, яка дорівнює одиниці (А + А¢ = 1).
 Наприклад: І — вуз Наприклад: І — вуз
А — економічний вуз А¢ = І — А (всі інші вузи, крім економічних, — технічні, гуманітарні, військові та ін.). Питання для самостійно ї роботи 1. Знайдіть поняття, які перебували б у відношенні тотожності з такими поняттями: перша голосна літера в українському алфавіті; рівносторонній трикутник і найбільша річка у Європі. 2. Чи є тотожними за обсягом поняття, що тотожні за змістом? Наведіть приклади. 3. По відношенню до даних понять знайдіть по два поняття, одне з яких було б підпорядкованим, друге підпорядковувало б його: «майор», «закон фізики», «проступок», «літературний твір». 4. Як співвідносяться між собою змісти підпорядкованого й підпорядковуючого понять? 5. Знайдіть поняття, обсяг якого частково збігався б з обсягом такого поняття: «лікар», «метал», «європейська держава», «учень». 6. Чи можна вважати поняття «море» і «озеро» частково збіжними на тій підставі, що в них є спільні ознаки? 7. Знайдіть поняття, підпорядковане даному, вказавши на універсальну множину (клас): «дієслово», «поняття», «акула», «автомобіль». 8. Встановіть відношення між обсягами таких понять, зобразивши їх графічно колами Ейлера: «новатор», «робітник», «спортсмен»; «близький», «далекий»; «автор опери «Пікова дама», «видатний український композитор»; «чорний», «нечорний»; «метал», «рідина», «ртуть»; «викладач», «неуспішність»; «кит», «риба», «ссавці». 9. За допомогою обмеження перетворити загальні поняття в одиничні: революція, задача, підручник. 10. За допомогою узагальнення перетворити одиничні поняття у загальні: найглибше озеро в світі; роздержавлення власності в Україні, швидкість світла. 11. Використовуючи найближчий рід, обмежте поняття: 1) письменник, 2) проступок, 3) війна. 12. Використовуючи найближчий рід, здійсніть узагальнення таких понять: 1) європейська держава; 2) українська мова, 3) трактор. 13. Розшифруйте, що означають символи: Dfd, Dfn. 14. Назвіть види визначень і наведіть приклади до них. 15. Назвіть приклади типових помилок при порушенні правил визначення через найближчий рід і видову відмінність. 16. Наведіть приклади прийомів, подібних до визначення. 17. Назвіть основні види поділу понять та сформулюйте їх правила. 18. Наведіть приклади наукових класифікацій. Тема 4. Судження Таблиця класифікації суджень
Модальні висловлювання. Модальна логіка є розділ сучасної логіки, де вивчаються модальні висловлювання та їхні відношення в структурі міркувань. Існують такі види модальних логік і модальних висловлювань: алетичні, епістемічні, темпоральні, деонтичні. Алетичні висловлювання включають такі модальності: «необхідно», «можливо», «випадково» та їх модифікації. Епістемічні висловлювання включають до свого складу такі модальності: «знаю», «вірю», «вважаю», «доведено», «відомо», «спростовано» тощо. Темпоральні висловлювання включають такі оцінки змісту, у яких необхідні уточнення з використанням часових характеристик: «було так, що», «буде так, що», «завжди було так, що», «завжди буде так, що», «раніше», «пізніше», «одночасно» та ін. Деонтичні висловлювання характеризують наявність або відсутність в судженні певних норм за допомогою таких модальностей: «обов’язково», «необов’язково», «дозволено», «недозволено», «заборонено», «незаборонено» та ін. (див. табл. класифікації суджень і табл. видів модальних логік і модальних висловлювань).
Таблиця видів модальних логік і модальних висловлювань
Схема взаємозв’язку суджень
3. Складні судження утворюються шляхом поєднання між собою простих суджень за допомогою логічних сполучників (кон’юнкції, виключаючої і невиключаючої диз’юнкції, імплікації та еквівалентності). Природною мовою названі логічні сполучники виражаються за допомогою граматичних сполучників «і», «та», «або-або», «або» («чи»), «якщо..., то…», «тоді і тільки тоді, коли...». 1) Єднальні (кон’юнктивні) судження — це такі судження, які утворені з двох суджень за допомогою сполучника «і» (або «та»). Дано деякі судження А та В. Припустимо, що вони семантично незалежні одне від одного, тобто істинність або хибність А не викликає істинності або хибності В, і навпаки. Тоді судження «А і В» є функцією істинності суджень «А» та «В». Це означає, що істинність або хибність судження «А і В» повністю визначається істинністю і хибністю складових його суджень А та В. Можливі такі комбінації кон’юнктивних суджень та їх результатів:
Єдиною умовою істинності кон’юнктивного судження є істинність обох складових цього судження. 2) Розділові (диз’юнктивні) судження бувають двох видів: а) виключаючо-розділові судження (строга диз’юнкція) — це такі судження, які утворюються з будь-яких двох інших суджень за допомогою логічного сполучника «або...або». Зміст цього сполучника полягає в тому, що він поєднує несумісні судження. ВРС істинне, коли одна зі складових частин істинна, а інша — хибна, і хибне, коли обидві складові частини його хибні.
б) невиключаючо-розділові судження (нестрога диз’юнкція) утворюються з будь-яких двох суджень за допомогою сполучника «або», що припускає сумісність суджень. НВРС істинне, коли істинні обидва його компоненти, або коли одне з них істинне, а друге — хибне. НВРС хибне тоді, коли є хибними обидва компоненти судження.
3) Умовні (імплікативні) судження утворюються з будь-яких двох інших суджень за допомогою логічного сполучника «якщо..., то...» Його формула: «Якщо А, то В». А називається основою, або антецедентом, В — наслідком, або консеквентом. Умовне судження хибне тоді, коли його основа — істинна, а наслідок — хибний, і істинне в усіх інших випадках.
Приклад: — якщо 2 × 2 = 4, то сніг білий (І) (І) (І) — якщо 2 × 2 = 5, то сніг білий (І) (X) (І) — якщо 2 × 2 = 5, то сніг чорний (І) (X) (X) — якщо 2 × 2 = 4, то сніг чорний (X) (І) (X) 4) Судження еквівалентності утворюється з будь-яких двох інших суджень за допомогою логічного сполучника «тоді і тільки тоді, коли...». Воно істинне, коли обидва складові судження є істинними або коли вони обидва є хибні, і хибне в усіх інших випадках.
Два судження називаються взаємозаперечними або суперечними одне одному, якщо одне з них істинне (І), а друге — обов’язково хибне (X). Взаємозаперечними є такі пари суджень:
1) А — О «Всі S є Р» і «Деякі S не є Р»; 2) Е — 1 «Жодне S не є Р» і «Деякі S є Р»; 3) «Це S є Р» і «Це S не є Р».
Заперечення бувають внутрішніми і зовнішніми. Внутрішнє заперечення означає невідповідність предиката суб’єктові. Зовнішнє — заперечення усього судження. Питання для самостійної роботи 1. Що означають такі логічні символи?
1.2. Ù 1.6. «1.10. Lр 1.3. Ú 1.7.А 1.11. Мр 1.4. «ù» 1.8.ÑА1.12. Dfd, Dfn 2. Визначте вид судження, його терміни та їх розподіленість у таких випадках: 2.1. Інколи люди спізнюються на роботу. 2.3. Деякі студентине є спортсменами. 2.4. Вода, нагріта до температури 80°С, не кипить. 2.5. Курчат рахують восени. 2.6. Всі громадяни України одержують приватизаційні чеки. 2.7. Деякі ліки бувають страшніші за самі хвороби. 2.8. Ніяка причина не може бути вибаченням за неввічливість. 2.9. Преса є четвертою владою. 2.10. Деякі люди не вивчають логіку. 3. Визначте суб’єкт, предикат і зв’я
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.106 (0.019 с.) |



 Тотожні
Тотожні
 Підпорядковані
Підпорядковані
 Перехресні (перетину)
Перехресні (перетину)
 Співпідпорядковані
Співпідпорядковані

 Протилежні
Протилежні


 Суперечні
Суперечні



 Тотожні
Тотожні
 Перехресні (перетину)
Перехресні (перетину)
 Суперечні
Суперечні
 Суперечні
Суперечні
 Формула доповнення: 1 — А = А¢
Формула доповнення: 1 — А = А¢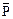 (x)]
(x)]

 1.1«=» 1.5. «®» 1.9. àА
1.1«=» 1.5. «®» 1.9. àА


