Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сили та напруження у вітках пасової передачіСодержание книги
Поиск на нашем сайте
Зусилля та напруження в пасі від його попереднього натягу. Для створення умов виникнення сил тертя між пасом та шківами пас треба одягти на шківи із деяким попереднім натягом. На рис. 21.11, а показана пасова передача у передпус–ковому стані, тобто без навантаження (ТІ = Т2 = 0) і в стані спокою. В цьому разі вітки паса навантажені тільки зусиллям попереднього натягу F0 яке спричинює в довільному поперечному перерізі площею А паса напруження попереднього натягу σ0 = F0/А. (7)
Зусилля та напруження в вітках при передаванні робочого навантаження. Після прикладення робочого навантаження (обертові моменти Т1 на ведучому шківі і Т2 на веденому шківі) зусилля у вітках паса змінюється (рис. 21.11, б): у ведучій вітці зусилля збільшується і стає F1 а у веденій зменшується і стає F2. За умовою рівноваги шківа маємо: Т1 = (F1 – F2) · d/2 або F1– F2 = Ft,(8) де Ft = 2Т1/d1 – колова сила на шківі, або корисне навантаження паса.
Зв'язок між F0, F1 та F2можна встановити з таких міркувань. Довжина паса не залежить від навантаження і залишається незмінною як у ненавантаженій, так і у навантаженій передачі. Відповідно додаткове витягування ведучої вітки компенсу–ється рівним скороченням веденої вітки. Тому збільшення зусилля у ведучій вітці на ∆F забезпечує зменшення зусилля у веденій вітці на ∆F (при лінійній залежності між силою та деформацією), тобто F1 = F0 + ∆F F2 = F0 – ∆F Записані два рівняння дозволяють дістати вираз F1+ F2 = 2F0. (9) Тепер із рівностей (8) та (9) випливає F1 = F0 + 0,5Ft; F2 = F0 – 0.5Ft. (10) Ці два рівняння виражають сили натягу ведучої та веденої віток залежно від сили попереднього натягу F0 та корисного навантаження Ft, але не розкривають тягової здатності передачі, яка пов'язана з силами тертя між пасом та шківами. Співвідношення сил натягів Fi ведучої та F2 веденої віток при роботі передачі (без урахування дії відцентрових сил) визначають за відомим рівнянням Ейлера, добутим для гнучкої нерозтяжної нитки, що ковзає по циліндричній поверхні. Розглянемо відрізок паса, який знаходиться на шківі і обмежений центральним кутом dφ (рис. 21.12).
На цей відрізок паса діють такі сили: dN – нормальна реакція шківа; F – біжуче значення натягу паса в перерізі, положення якого визначає кут φ; F + dF – натяг паса в перерізі з координатою φ + dφ; fdN – сила тертя на даний відрізок паса (f – коефіцієнт тертя між пасом та шківом).
Нехтуючи товщиною паса, запишемо умову рівноваги даного відрізку паса; [F + f dN – (F + dF)] d/2 = 0 або f dN = dF; dN – F sin (dφ/2) – (F + d F) sin(dφ/2) = 0. Відкидаючи у другій умові рівноваги члени другого порядку малості (dF sin (dφ/2) ≈ 0) та беручи sin (dφ/2) ≈ dφ/2, дістаємо dN = Fdφ. Запишемо співвідношення dF/F = f dφ. Інтегруючи ліву частину рівності від F2 до F1, а праву – від 0 до α, дістанемо:
Отже, маємо співвідношення між зусиллями у вітках паса з урахуванням сили тертя між пасом та шківом: F1 = F2e f α, (11) де е – основа натурального логарифму; α– кут обхвату; f– приведений коефіцієнт тертя. Співвідношення (11) називають формулою Ейлера. Розв'язуючи сумісно рівняння (10) та (11), матимемо:
Формули (12) визначають зв'язок сил натягу віток навантаженої силою Ft пасової передачі з факторами тертя f і α. Цей зв'язок справедливий за умови знаходження паса на грані буксування на шківі, тобто коли дуга ковзання β дорівнює дузі обхвату шківа α. Інакше кажучи, формули (12) визначають граничні співвідношення між зусиллями в пасі. Якщо у формули (12) замість α підставити значення дуги ковзання β, то дістанемо не граничні, а біжучі, або робочі, значення натягу віток паса. Напруження в поперечних перерізах ведучої та веденої віток можна знайти, поділивши праві та ліві частини рівнянь (10)1 на площу А перерізу паса: σ1 = σ 0 + 0,5 · σt, σ 2 = σ 0 – 0,5 · σt, (13) де σt = Ft /A – напруження в пасі від робочого навантаження (корисне напруження в пасі). Зусилля та напруження в пасі від дії відцентрових сил. Рух паса по криволінійних траєкторіях (на шківах) обумовлює появу відцентрових сил, які додатково навантажують пас Для визначення натягу паса F v від дії відцентрових сил (рис. 21.13) виділимо елемент паса завдовжки dl = r · dφ iрозглянемо рівновагу цього елемента.
Маса елемента паса dm = ρ·A·dl = ρ·A·r·dφ, де ρ – густина матеріалу паса. На даний елемент паса діє відцентрова сила Nν = (ν2/r) · dm = ρ·A·ν2 ·dφ та спричинені цією силою зусилля додаткового натягу Fν (рис 13) Проекціюючи всі діючі сили на напрям Nν,запишемо умову рівноваги
Nν – 2Fν · sin · (dφ/2) = О Якщо взяти sin (dφ/2) ≈ dφ/2 та підставити значення Nν,то дістанемо ρ·A·ν2 · dφ – 2Fν · dφ/2 = 0. Із цього рівняння матимемо формулу для визначення додаткового натягу паса від дії відцентрових силі Fν = ρ·A·ν2 . (14) Відповідно напруження у поперечних перерізах паса від дії на нього відцентрових сил συ = 10–6 ρν2 (15) У формулах (14) та (15): ρ – у кілограмах на кубічний метр (кг/м3); ν – у метрах на секунду (м/с); A– у квадратних метрах (м2); σν– у мегапаскалях (МПа); Fν– у ньютонах (Н). Із формул (14) та (15) видно, що зусилля Fνта напруження σν від дії відцентрових сил не залежать від діаметрів шківів і однакові для всіх поперечних перерізів паса. Відмітимо, що дія відцентрових сил негативно впливає на тягову здатність пасової передачі, оскільки ослаблюється притискання паса до шківів. Якщо Fν ≥ F0 або σν ≥ σ0 , то зникає взаємодія паса зі шківами. Критична швидкість паса визначається з умови συ = σ0 [10]
Для стандартних клинових пасів, які мають густину ρ = 1150 кг/м3 і мінімальне рекомендоване напруження попереднього натягу σ0 = 1,2 МПа, υ кр = 32,3 м/с. Якщо швидкість клинового паса ν< 10 м/с, то Fν ≤ 0,l F0 min. Шкідлива дія відцентрових сил на тягову здатність пасової передачі зменшується використанням відповідних натяжних пристроїв. Напруження від згину паса на шківах. При обгинанні шківів у перерізах паса виникають напруження згину (рис. 21.14).
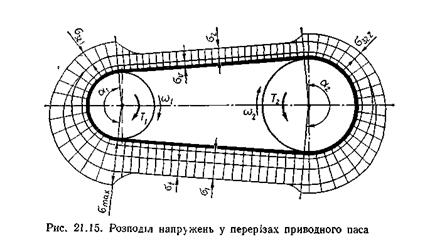
У плоскому пасі нейтральний шар у перерізі збігається з середнім шаром і найбільші напруження згину можна визначити за відомою з курсу опору матеріалів формулою σзг = Е(уmax/R). Враховуючи, що радіус кривини нейтрального шару паса R ≈ d/2, авідстань максимально віддалених точок перерізу паса від нейтрального шару уmах = δ/2, дістанемо формулу для визначення напружень згину в пасі: σзг = Е · δ/2, (17) де Е– модуль пружності матеріалу паса. Основним фактором, який визначає напруження згину, є відношення товщини паса δ до діаметра шківа d. Чим менше це відношення, тим менше напруження згину у пасі. Сумарні напруження в перерізах паса. Вище було встановлено, що в усіх перерізах паса навантаженої передачі діє однакове напруження σv; у перерізах ведучої вітки мають місце напруження σ1 а у перерізах веденої вітки – напруження σ2, різниця між якими дорівнює напруженню σt від корисного навантаження; у перерізах відрізків паса, розміщених на шківах, діють відповідні напруження σЗГ1 та σЗГ2. За цими складовими напружень можна побудувати діаграму розподілу напружень по довжині паса (рис. 21.15). Із діаграми розподілу напружень видно, що максимальне напруження має місце у ведучій (нижній) вітці в тому перерізі паса, який набігає на менший ведучий шків:
σмах = σІ + σv + σзгl = σ0 + 0,5·σt + σv + σзгl (18) Мінімальне напруження виникає у перерізах веденої (верхньої) вітки паса: σміn = σ2 + σv = σ0 – 0,5·σt + σv(19) Оскільки пас рухається відносно шківів, напруження в його окремому поперечному перерізі не залишається постійним у часі. Характер зміни в часі сумарного напруження у довільному перерізі паса наведено на рис. 21.16.
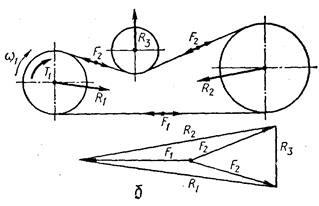
Навантаження на вали пасової передачі. Сили натягу віток паса передаються на вали передачі та їхні опори. Відповідно до рис. 21.17, а рівнодійну Rсил натягу F1 та F2 віток можна визначити за формулою
Дію відцентрової сили тут у розрахунках можна не враховувати, оскільки при середніх швидкостях паса вона незначна і спричинює лише розвантаження валів (відцентрова сила зрівноважується у пасі). У пасових передачах із натяжним роликом або у багатошківних передачах навантаження на вали доцільно визначати графічним способом за допомогою побудови плану сил (рис. 21 17, б ).
Для цього треба накреслити у певному масштабі схему пасової передачі і попередньо визначити у вітках зусилля Fl та F2.3 довільної точки на плані сил зображають напрями дії сил F1та F2 (паралельно напрямам віток передачі у бік їхнього руху) і відкладають у масштабі на цих напрямах сили. Якщо з'єднати кінці відрізків, що зображають сили Ft та F2,то дістанемо напрям і у вибраному масштабі значення сил, якими навантажуються вали пасової передачі.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.240 (0.011 с.) |





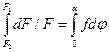 ; ln (F1/F2) = f α; F1/F2 = е f α.
; ln (F1/F2) = f α; F1/F2 = е f α. ;
;  ;
;  . (12)
. (12)
 (16)
(16)

 (21.20)
(21.20)