Оцінка міцності деталей при простих деформаціях

Найрозповсюдженішим методом оцінки міцності деталей машин є порівняння розрахункових напружень, які виникають у деталях при дії експлуатаційних навантажень, із допустимими напруженнями для призначеного матеріалу цих деталей.

У загальному вигляді умови міцності записують такими співвідно­шеннями:

σ ≤ [σ] або τ ≤ [τ], (1)

де σ, [σ] – відповідно розрахункове і допустиме нормальне напру­ження;

τ, [τ] – те саме, дотичне напруження.

Розрахункове напруження визначається залежно від виду дефор­мації в небезпечному перерізі деталі. Приклади простих видів дефор­мації деталей показані на рис. 4.1.

Умови міцності з урахуванням виду деформації записують у такому вигляді:

 

при осьовому розтягу (рис. 4.1, а) або стиску σ_p = F/A ≤ [σ]_р; (2)

при згині (рис. 4.1, б) σ = M/W₀ ≤ [σ]; (3)

при крученні (рис. 4.1, в) τ = T/W_p ≤ [τ]; (4)

при поверхневому зминанні деталей (рис. 4.1, г) σ_зм = F/ A ≤ [σ ]_зм; (5)

при зсуві або зрізі (наприклад, для циліндричного пальця на рис. 4.1, д)

τ _з = F/A ≤ [τ]_з; (6)

У записаних формулах взято такі позначенняі F – сила; М – згинальний момент; Т – крутний момент; А – площа перерізу (поверхні зминання); W₀ – осьовий момент опору перерізу; Wp – по­лярний момент опору перерізу деталі.

Для розповсюджених форм перерізів деталей момент опору визна­чають за формулами:

круглий переріз діаметром d

W₀ = π·d ³/32 ≈ 0,1d ³; W_р = π·d ³/16 ≈ 0,2d ³;

прямокутний переріз із розмірами b x h (сторона з розміром h пер­пендику–лярна до нейтральної осі О – О перерізу)

W₀ = b·h²/6.

При одночасній дії в перерізі деталі напружень згину, розтягу (стиску) і кручення на основі гіпотези найбільших дотичних напру­жень для сталевих деталей визначають еквівалентне напруження, а умову міцності записують у вигляді

(7)

Крім звичайних видів руйнування деталей, спричинених розгля­нутими вище деформаціями, на практиці мають місце випадки лока­лізованого руйнування їхніх поверхонь. Це руйнування пов'язане з контактними деформаціями і напруженнями.

Розглянемо деякі положення до розрахунку контактної міцності деталей без виведення основних формул, які даються в курсі «Тео­рія пружності», що будемо використовувати надалі як вихідні за­лежності для розрахунків на міцність деяких деталей машин.

Контактні напруження виникають у зоні контакту двох деталей у тому разі, коли контакт початково ненавантажених деталей здій­снюється по лінії або в точці (стиск двох циліндрів із спільною твір­ною, циліндра і площини, двох сферичних поверхонь та ін.).

Якщо контактні напруження більші за допустимі, то на поверх­нях деталей можуть виникнути вм'ятини, борозни або дрібні ракови­ни. Подібні пошкодження спостерігають на робочих поверхнях зуб­ців зубчастих коліс, на бігових доріжках кілець підшипників кочен­ня, на колесах і рейках рейкових транспортних засобів та ін.

Для двох характерних випадків умови контактної міцності та ін­ші розрахункові залежності записують так:

1. Початковий контакт деталей по лінії (два циліндри з пара­лельними осями, циліндр та площина). На рис. 4.2, а показано при­клад навантаження двох циліндрів контактним тиском q_н = F_н / ℓ_к.

Під навантаженням лінійний контакт перетворюється в контакт по вузькій площині. В цьому разі максимальне контактне напруження визначають за формулою Герца і відповідно умову контактної міцності записують у вигляді

, (8)

де Z_M – коефіцієнт, який враховує механічні властивості матеріалів деталей, що знаходяться в контакті; ρ_зв – зведений радіус кривини поверхонь деталей у зоні їхнього контакту.

Коефіцієнт , (9)

де Е₁ і Е² – модулі пружності матеріалів деталей; μ₁ і μ₂ – відповідно коефіцієнти Пуассона.

Якщо деталі виготовлені з однакового матеріалу (Е₁ = Е₂ = Е і μ₁ = μ₂ = μ), то коефіцієнт Z_M можна визначити за спроще­ною формулою

. (9а)

Для окремого випадку сталевих деталей (Е = 2,15·10⁵ МПа; μ = 0,3) дістанемо Z_M == 275 МПа^1/2.

Зведений радіус кривини поверхонь деталей визначають за спів­відношеннями (знак плюс для зовнішнього контакту за рис. 4.2, а і знак мінус для внутрішнього контакту за рис. 4.2, б)

1/ρ_зв = 1/ρ₁ ± 1/ρ₂, (10)

У випадку контакту циліндра радіусом ρ₁ з площиною (ρ₂ = ∞) маємо ρ_зв = ρ₁.

Умова контактної міцності (8) справедлива не тільки для круго­вих, а й для довільних циліндричних поверхонь деталей. Для останніх ρ₁ і ρ₂ будуть радіусами кривини цих поверхонь у точках їхнього контакту.

2. Початковий контакт деталей у точці (дві кулі, куля і площина).

У разі стискання двох куль силою F_H (рис. 4.2, б) точковий контакт перетворюється в контакт по круговій площині. При цьому максималь­не напруження в зоні контакту і відповідна умова контактної міцнос­ті мають вигляд

, (11)

де Z'_M – коефіцієнт, який враховує механічні властивості матеріа­лів деталей;

р_зв – зведений радіус кривини поверхонь деталей.

Коефіцієнт . (12)

В окремому випадку, коли деталі виготовлені з однакового матеріалу

(Е₁ = Е₂ = Е і μ₁ = μ.₂ = μ), коефіцієнт Z'_M можна визначити за спрощеною формулою

. (12а)

Для сталевих деталей маємо Z^*_M = 1755 МПа^2/3.

Розглянуті вище залежності дозволяють визначити розрахункові напруження в перерізах деталей або на поверхні їхнього контакту за діючими навантаженнями і конкретними розмірами деталей. Щоб дістати значення допустимих напружень, потрібно знати характер зміни діючих напружень у часі і з урахуванням цього характеру, а також механічних характеристик матеріалу деталей можна визначи­ти граничні напруження і відповідні їм допустимі напруження.

Зміна напружень у часі

Під час дії на деталь постійного за модулем та напрямом наванта­ження в ній виникають постійні напруження. Якщо модуль або на­прям навантаження щодо деталі змінюється в часі, то і напруження в деталі будуть мінятися в часі. Наприклад, змінні в часі напруження будуть тоді, коли навантаження постійне, але змінюється положення деталі щодо напряму навантаження (постійна за модулем і напрямом поперечна сила на вісь, що обертається, спричинює в перерізах цієї осі змінні в часі напруження).

Змінні напруження, що виникають у деталях машин, у більшості випадків змінюються в часі періодично.

На рис. 4.3 показаний гра­фік можливої періодичної зміни нормального σ чи дотичного τ на­пруження в часі t.

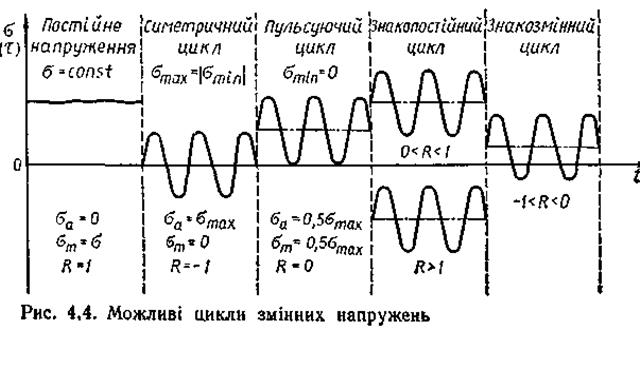
Сукупність всіх напружень за один період зміни їх називається циклом напружен ь. Цикл напружень характеризується максимальним σ_max і мінімальним σ_min напруженнями, а також амплітудою напружень σ_а та коефіцієнтом асиметрії циклу R. Середнє напруження σ_m циклу дорівнює алгебраїчній півсумі максимального і мінімального напружень:

σ_m = 0,5(σ_max + σ_min). (13)

Амплітуда напружень σ_a циклу –це алгебраїчна піврізниця максимального та мінімального напружень:

σ_a = 0,5(σ_max – σ_min). (14)

Відношення мінімального напруження циклу до максимального, взяте з відповідним знаком, називається коефіцієнтом асиметрії циклу

R = σ_min/σ_max. (15)

Практичне застосування в розрахунках деталей машин знаходять: постійне напруження (σ_m = σ; σ_а = 0; R = 1), симетричний (σ_m = 0; σ_а = σ_max; R = –1) і пульсуючий (σ_m = 0,5σ_max; σ_а = 0,5·σ_max; R = 0) цикли напружень. Усі інші цикли напружень можуть бути зведені до певної сукупності названих трьох циклів.

Відомо, що змінні напруження спричинюють явища втоми матері­алу деталей. Характеристикою міцності матеріалу в цьому випадку виступає границя витривалості σ_R (відповідно σ_–1, τ_–1 для симетрич­ного і σ₀, τ₀ для пульсуючого циклів).