

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
в) Миттєва зміна ємності С кола
Содержание книги
- Топливо. Классификация по агрегатному состоянию и способу получения.
- Горючая масса. Элементарный состав. Пересчет с сухой и раб массы на горючую.
- Летучие вещества, кокс, полукокс. Классификация кокса.
- Газообразное топливо. Горючая и негорючая части.
- Теплота сгорания. размерность. Связь между низшей и высшей теплотой сгорания
- лабораторные способы определения теплоты сгорания твердого и тяжелого жидкого топлива
- Расчетные методы определения теплоты сгорания твердого, жидкого и газообразного топлива
- Теоретический массовый расход кислорода на горение топлива
- Состав продуктов полного сгорания твердого и жидкого топлива.
- Теоретический объем водяных паров образующихся при сгорании 1 кг твердого и жидкого топлива
- Действительная масса газообразных продуктов сгорания (кроме сланцев).
- Теоретический обьем вод пара в продуктах горения газообразного топлива (при d≠13 г/м3 и d=13 г/м3)
- Уравнение полного горения твердого и жидкого топлива
- определение коэффициента расхода воздуха при полном сгорании топлива
- Загальна характеристика палива
- Волога, що міститься в паливі, підрозділяється на гігроскопічну
- багатофазні кола та системи а) симетричне , несиметричне
- багатофазні кола та системи б) зрівноважене, незрівноважене
- Розрахунок несиметричних 3-фазних кіл
- Трифазна потужність і її вимірювання
- Алгоритм розрахунку перехідних процесів класичним методом.
- А) Підключення кола R, l до джерела постійної напруги;
- В) Підключення кола R, l до джерела синусоїдної напруги.
- б) коротке замикання кола R, С;
- Перехідні процеси у колі R,L,C
- Перехідні процеси при миттєвій зміні параметрів ділянок ел.кіл
- в) Миттєва зміна ємності С кола
- Пряме перетворення Лапласа та його властивості
- Алгоритм розрахунку оригіналу ф-ції за її відомим операторним зображенням
- Розрахунок перехідних процесів при дією ЕРС складної форми. Інтеграл Дюамеля.
- Коефіцієнти що характеризують періодичну несинусоїдну функцію
- Характеристика 4-полюсників, їх клас-ція
- Рівняння пасивного чотириполюсника в Y,Z,A, іB формах
- Заступні схеми пасивного чотириполюсника.
- Повторний опір пасивного чотириполюсника
- Закони і рівняння магнітного кола (аналоги законів Ома і Кірхгофа).
Розглянемо електричне коло. Розрахуємо струм перехідного процесу вважаючи відомими параметри пасивних елементів та вхідну постійну напругу U. 1. До комутації ємність C2 у коло не було увімкнено, тому:  =U =U  =0 ; 2. Перехідний процес у колі закінчиться, коли обидві ємності зарядяться до напруги джерела: =0 ; 2. Перехідний процес у колі закінчиться, коли обидві ємності зарядяться до напруги джерела:  =U; 3. Характеристичне рівняння і його корінь: R+1/p(C1+C2)=0 ; p=-1/R(C1+C2); Оскільки розглядається коло першого порядку і характеристичне рівняння має один корінь, вираз вільної складової напруги на ємності буде таким: =U; 3. Характеристичне рівняння і його корінь: R+1/p(C1+C2)=0 ; p=-1/R(C1+C2); Оскільки розглядається коло першого порядку і характеристичне рівняння має один корінь, вираз вільної складової напруги на ємності буде таким:  =Aept, а напруга перехідного процесу у загальному вигляді : =Aept, а напруга перехідного процесу у загальному вигляді :  = =  + + 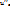 =U+Ae–(1/R(C1+C2)t ; 4.Розрахунок сталої інтегруванняз умови незмінності наруги на ємності в момент комутації неможливий, тому що безпосередньо до комутації напруги на ємностях були різними, а безпосередньо після комутації – вони однакові, оскільки у цьому режимі ємності з’єднані паралельно. Отже в момент комутації напруги на ємностях змінюються стрибкоподібно, що призводить до появи у гілках з ємностями нескінченно великих струмів. Нехтуючи за цих умов скінченним вхідним струмом, рівняння кола для інтервалу комутації (0_ <t<0+) на підставі першого закону Кірхгофа запишемо так: C1(duc1/dt)=-C2(duc2/dt) ; Інтегруємо його в інтервалі комутації . =U+Ae–(1/R(C1+C2)t ; 4.Розрахунок сталої інтегруванняз умови незмінності наруги на ємності в момент комутації неможливий, тому що безпосередньо до комутації напруги на ємностях були різними, а безпосередньо після комутації – вони однакові, оскільки у цьому режимі ємності з’єднані паралельно. Отже в момент комутації напруги на ємностях змінюються стрибкоподібно, що призводить до появи у гілках з ємностями нескінченно великих струмів. Нехтуючи за цих умов скінченним вхідним струмом, рівняння кола для інтервалу комутації (0_ <t<0+) на підставі першого закону Кірхгофа запишемо так: C1(duc1/dt)=-C2(duc2/dt) ; Інтегруємо його в інтервалі комутації . 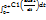 = - = - 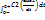 чи чи 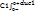 = - = - 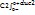 . У результаті отримуємо: C1[uc1(0+)-uc1(0-)]=C2[uc2(0+)- . У результаті отримуємо: C1[uc1(0+)-uc1(0-)]=C2[uc2(0+)-
uc2(0-)]; Вираз у квадратних дужках — стрибок ємнісної напруги в момент комутації на кожній з ємностей: C1Δuc1(0)=-C2Δuc2(0) чи ΔQ1(0)+ ΔQ2(0)=0;Розрахунком доводиться, що заряд кожної ємності окремо в момент комутації змінюється, а сумарний заряд ємностей залишається незмінним. Це відповідає другому закону комутації. Визначимо початкову умову з попередньої формули, урахувавши: а) безпосередньо до комутації напруги на ємностях були такими: «uc1(0-)=U; uc2(0-)=0; б) безпосередньо після комутації напруги на ємностях будуть однаковими: uc1(0+)=uc2(0+)uc(0+); Отже, C1[uc(0+)-U]=-C2uc(0+); Uc(0+)=U(C1/C1+C2); Тепер із напруги перехідного процесу визначимо сталу інтегрування: U(C1/C1+C2)=U+A; звідки .A=U(C1/C1+C2)-U=-U(C2/C1+C2). Підставимо сталу інтегрування донапруги перехідного процесу і остаточно отримаємо: Uc=U-U(C2/C1+C2)e-[1/R(C2+c2)]t ; Проаналізуємо особливості енері'епічного процесу кола в момент комутації. Для цього розрахуємо запас енергії в електричному полі кола безпосередньо до комутації Wc (0_) та безпосередньо після комутаціїWc (0+) і порівняємо їх: Wc(0-)=Q2/2C1; Wc(0+)=Q2/2(C1+C2); Як бачимо, Wc(0+) <Wc(0-), тобто, як і у попередньому випадку (Д1ІВі підрозд. 11.8.2), у колі в момент кому тації відбуваються необоротні втрати енергії. Енергія втрачається під час проходження нескінченно великих струмів через провідники з нескінченно малими опорами.
|