Перехідні процеси у колі R,L,C

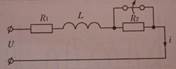
А) Підключення кола R,L,C до джерела постійної напруги:

Проаналізуємо перехідний процес у колі, вважаючи, що ємність до початку перехідного процесу не була заряджена. 1.До комутації у колі існував усталений режим, який характеризувався відсутністю струму та напруги на пасивних елементах: I_=0; u_C-=0 ;   uc-                           ежим, який характеризувався відсутністю струму та напруги на пасивних елементахж2. Унаслідок комутації коло підмикається до джерела ЕРС, і в ньому починається процес зарядження ємності.Він припиняється, коли ємність зарядиться до напруги джерела, тому усталений режим у скомутованому колі буде характеризуватися: I’=0; u’_c=E ; 3.Характер вільного режиму залежить від параметрів кола і відповідно від коренів характеристичного рівняння. Якщо корені характеристичного рівняння дійсні і різні, то відбувається аперіодичний процес. У такому разі вільну складову напруги на ємності запишемо відповідно f’’(t)=A₁e^P1t+ A₂e^P2t; а загальний вигляд закономірності, за якою змінюється ця напруга буде таким: u_C=u_C’ + u_C’’= E+( A₁e^P1t+ A₂e^P2t) ; струм

 

кола: i=Cdu_C/dt=C(p₁A₁e^P1t+ p₂A₂e^P2t) ; 4.Для розрахунку двох сталих інтегрування (А₁ та А₂) необхідні дві початкові умови, які є незалежними і нульовими: i(0_)= i(0+)= 0 ; u_C(0_)= u_C(0+)= 0 ;Запишемо i=Cdu_C/dt=C(p₁A₁e^P1t + p₂A₂e^P2t) для моменту часу t=0₊ : 0=E+A₁+A₂ ;                                                                             O=C(p₁A₁+p₂A₂) . Розв’язання цієї системи відносно сталих інтегрування дає: A₁=p₂E/p₁-p₂;                                                            A₂=p₁E/p₁-p₂ ; Порівнявши отриманий результат з попер формулою доходимо висновку, що струм перехідного процесу буде таким самим як і в аперіодичному процесі у разі розрядження ємності через коло L,Rале з протилежним знаком. Таке зауваження стосується і напруг на реактивних елементах. Напруга на ємності, окрім того, ще має й вимушену складову, що дорівнює ЕРС джерела живлення. Такий висновок справедливий також і для межі аперіодичного процесу та для коливального процесу.

Б) Коротке замикання кола R,l,C:

На схемі джерело ЕРС_e(t)=E=const,а ключ перемикається із положенням 1 у положення 2. 1) .До комутації у колі існував усталений режим, який характеризувався відсутністю струму, а напруга на ємності дорівнювала ЕРС джерела: i_=0; u_C-=E ; 2). Унаслідок комутації коло відмикається від джерела ЕРС і закорочується. У ньому виникає розряд ємності через ділянку R,L. Цей процес припиниться, коли ємність буде характеризуватися: I’=0; u’_c=0 ; 3. Характер вільного режиму залежить від параметрів кола і, відповідно від коренів характеристичного рівняння. Аперіодичний процес-корені хар. Рівняння дійсні й різні.У цьому разі вільну складову на ємності запишемо відповідно до f’’(t)=A₁e^P1t+ A₂e^P2tа загальний вигляд закономірності, за якою ця напруга змінюється, буде таким: u_C=u_C’ + u_C’’=A₁e^P1t+A₂e^P2t ; Струм кола i=Cdu_C/dt=C(p₁ A₁e^P1t+p₂ A₂e^P2t); Якщо корені хар. рівняння дійсні і однакові, то маємо межу

 

аперіодичного процесу. У цьому разі вільну складову напруги на ємності запишемо до f’’(t)=(A₃^t+A₄t)e^-δt ; Струм кола i=Cdu_C/dt=C[δ₁A₃+(1+δt)A₄)e^-δt ; 4.Для розрахунку двох сталих інтегрування (А₁ та А₂) необхідні дві початкові умови: i(0_)= i(0+)= 0 ; u_C(0_)= u_C(0+)= 0 ; Запишемо струм кола та струм напруги як : E=A₁+A₂ ; O=C(p₁A₁+p₂A₂); Розв’язання цієї системи відносно сталих інтегрування дає: A₁=p₂E/p₁-p₂; A₂=p₁E/p₁-p₂; Підставимо сталі інтегрування до напруги і отримаємо : U_c=-(E/p₁-p_2*(p₂e^P1t+p₁ e^P2t)); i=-(E/L(p₁-p₂)_*(e^P1t+e^P2t)); u_L=Ldi/dt=-(E/p₁-p_2*(p₂e^P1t+p₁ e^P2t)). Для розрахунку двох сталих інтегрування (А₃ та А₄) необхідні дві початкові умови. Вони такі самі, як і для аперіодичного процесу : i(0_)= i(0+)= 0 ; u_C(0_)= u_C(0+)= E; Запишемо напругу та струм кола для моменту часу t=0: E=A₃ ; 0=C(-δA₃ +A₄); Розв’язання цієї системи відносно сталих інтегрування дає: A₃=E; A₄=δE ; Підставимо сталі інтегрування до напруги і отримаємо : u_c=E(1+δt)e ^–δt : i=-E/L(te^–δt); u_L=-E(1-δt)e ^–δt ;