б)                коротке замикання кола R, С;

б)                коротке замикання кола R, С;

У схемі рис. 11.7, (а) ключ перемикається із положення «1» у положення «2». 1) Вважатимемо, що до комутації коло з послідовним з’єднанням еле­ментів R та С було підімкнено до джерела постійної ЕРС. Тому в нескомутованому колі струму не було, а напруга на ємності дорівнювала ЕРС джерела живлення u_C-=E. 2) У результаті комутації елементи R та С відмикаються від джерела і коло стає короткозамкненим. У ньому відбувається процес розрядження ємності через опір, який закінчиться тільки тоді, коли ємність повністю розрядиться, тобто u’_C=0. 3) Закон, за яким змінюється напруга на єм­ності у перехідному процесі в розглядуваному колі, запишемо так:u_C=u_C’ + u_C’’= Ae^-(1/RC)t . 4) Початкова умова визначається за другим законом комутації: u_C(0_)= u_C(0+)= E ; Для моменту часу t = 0+ як Е = А, одержимо сталу інтегрування, підстановкою якої отримаємо остаточний розв’язок задачі відносно напруги на ємності u_C=Ee^-(1/RC)t . Струм у цьому колі: i=Cdu_C/dt=-(E/R) e^-(1/RC)t

в)                підключення кола R, С до джерела синусоїдної напруги.

Тепер у схемі на рис. 11.7, (а) ідеальне джерело ЕРС е(t) = E_msin(wt + Ψ_e),відповідна напруга u(t) = е(t)=U_msin(wt=Ψ_u), a ключ перемикається із положення «0» у положення «1». Проаналізуємо перехідний процес у ко­лі, використовуючи той же алгоритм, що й раніше. 1). Будемо вважати, що до комутації у колі існував усталений режим, що характеризувався відсутністю струму та напруги на пасивних елементах кола:u_C_=0. 2). Після комутації у колі буде струм вимушеного режиму, розрахувати який краще у комплексній формі: 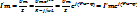 .Миттєве значення струму вимушеного режиму:i’=I’_msin(wt+Ψ_u- φ), а відповідна йому напруга на ємності: u’_C=(I’_m/wC)sin(wt+Ψ_u- φ-п/2); 3). Закон, за яким змі­нюється напруга на ємності у перехідному процесі, запишемо так: u_C= u_C’ + u_C’’= (I’_m/wC)sin(wt+Ψ_u- φ-п/2)+Ae^-(1/RC)t ; 4). Одна початкова умова визначається за другим законом комутації: u_C(0_)= u_C(0+)= 0; Для моменту часу t= 0+: 0= (I’_m/wC)sin(Ψ_u- φ-п/2)+A , одержимо сталу

 

інтегрування: A= -(I’_m/wC)sin(Ψ_u- φ-п/2) ; Розв’язок задачі стосовно напруги на ємності отримаємо, підставивши сталу інтегрування: u’_C=(I’_m/wC)sin(wt+Ψ_u- φ-п/2)- (I’_m/wC)sin(wt+Ψ_u- φ-п/2)e^-t/τ ;При цьому струм кола у перехідному процесі: i=C(du_C/dt)=I’_msin(wt+Ψ_u- φ)+ (I’_m/wCR)sin(Ψ_u- φ-п/2)e^-t/τ .З виразів випливає, що вільні складові струму і на­пруги на ємності за заданих U_miZ залежать від початкової фази Ψ_u (фа­зи вмикання) вхідної напруги, яка, в свою чергу, визначається моментом спрацьовування ключа. Вмикання ключа за умови Ψ_u- φ=±п/2призведе до того, що вільного струму та вільних складових напруг на ділянках кола не буде, тобто одра­зу після вмикання настане усталений режим. Якщо ж у момент вмикання Ψ_u- φ= 0, то початкові значення вільних складових струму і напруги будуть найбільшими і якраз у цьому випадку слід чекати надструмів і перенапруг.