В)                Підключення кола R, l до джерела синусоїдної напруги.

Нехай у схемі рис. 11.2,(а) ідеальне джерело ЕРС е(t) = E_msin(wt + Ψ_e), відповідна напруга u(t) = е(t)=U_msin(wt=Ψ_u), а ключ перемикається із по­ложення «0» у положення «1». Проаналізуємо перехідний процес у колі, використовуючи той же алгоритм, що і раніше. 1.) До комутації:    i_=0. 2).Після комутації (t ∞)у колі буде струм вимушеного режиму, роз­рахувати який краще у комплексній формі: 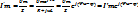.Миттєве значення струму вимушеного режимуi’=I’_msin(wt+Ψ_u- φ) 1).Закон, за яким змінюється струм перехідного процесу в розглядуваному колі за зазначених умов, запишемо так:і = і' + і" = I’_msin(wt+Ψ_u- φ)+ Ae^-(R/L)t . 2). Для визначення сталої інтегрування А необхідно знати початкові умови. У цьому випадку - це одна початкова умова, яку можна визначити за першим законом комутації:і(0_) = i(0+) = 0. Для моменту часу t = 0+ : 0= I’_msin(Ψ_u- φ)+ A , одержимо сталу інтегрування А = -I’_msin(Ψ_u- φ)+ AОтже, i’=I’_msin(wt+Ψ_u- φ) -I’_msin(Ψ_u- φ)e^-(R/L)t .Вираз напруги на індуктивності отримаємо за відомим співвідношенням u_L=Ldi/dt=wLI’_msin(wt+Ψ_u-φ+п/2)+RI’_msin(Ψ_u- φ)e^-(R/L)t . Напруга на опорі R : u_R = iR = R [I’_msin(wt+Ψ_u- φ) -I’_msin(Ψ_u- φ)e^-(R/L)t ] . З виразів випливає, що вільна складова струму і напруг за зада­них U_m і Z залежить від початкової i вхідної на­пруги, яка, в свою чергу, визначається моментом спрацьовування ключа. Вмикання ключа за умови Ψ_u- φ= 0 призводить до того, що вільного струму та вільних складових напруг на ділянках кола не буде, тобто одра­зу після вмикання буде усталений режим, у якому i= I’_msinwt;u_L=wLI’_msin(wt+Ψ_u +п/2)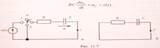

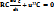2.5. Перехідні процеси у колі R, C:

Аналізуючи перехідний процес у колі (рис. 11.7, а), з рівняння Ri+u_C=e(t),складеного за другим законом Кірхгофа, слід вилучити струм і, щоб звес­ти його до рівняння відносно змінної стану u_C-.Для цього використаємо співвідношення і = Cdu_C/dtі отримаємо: Схему вільного режиму зображено на рис. 11.7, б і йому відповідає однорідне диференціальне рівняння :  .Xарактеристичне рівняння : RCp +1=0 має один корінь р =-1/RC, отже, загальний розв’язок диференціального рівняння: u_C’’=Ae^-(1/RC)t= Ae^-t/τ , де τ=RC- стала часу кола, що аналізується.

 

а)                підключення кола R, С до джерела постійної напруги:

Нехай у схемі рис. 11.7, а джерело ЕРС e(t) = Е = const, а ключ пере­микається із положення «0» у положення «1». Проаналізуємо перехідний процес, користуючись відомим алгоритмом. 1. До комутації у колі існував усталений режим, який характеризував­ся відсутністю струму та напруги на опорі R. Щодо напруги на ємності, то тут можливі варіанти: заряд ємності; до комутації ємність заряду не мала: u_C-= 0;тобто її на­пруга за час перехідного процесу збільшується від нульового значення до величини, що дорівнює ЕРС джерела живлення. дозаряд ємності; до комутації ємність була заряджена від стороннього джерела у поляр­ності, що відповідає напряму джерела ЕРС кола -u_c-=Uo.На­пруга теж збільшується від нульового значення до величини, що дорівнює ЕРС джерела живлення, однак, ураховуючи різний початковий стан та полярність їх напруг у мо­мент комутації, доходимо висновку, що перехідний процес для варіанта 2 за своєю фізичною сутністю є дозарядженням ємності.

перезаряд ємності;до комутації ємність була заряджена від стороннього джерела у поляр­ності, протилежній до напряму джерела ЕРС кола -u_c-=-Uo.На­пруга теж збільшується від нульового значення до величини, що дорівнює ЕРС джерела живлення, однак, ураховуючи різний початковий стан та полярність їх напруг у мо­мент комутації, доходимо висновку, що перехідний процес для варіанта 3 за своєю фізичною сутністю є перезарядженням ємності. 1. У вимушеному режимі після комутації (t ∞)незалежно від варіан­тів режиму нескомутованого кола струм та напруга на опорі R відсутні, оскільки ємність не пропускає струму за постійної напруги (і = С du_C/dt), а напруга на ємностіu_C’=E;2.Закон, за яким змі­нюється напруга на ємності у перехідному процесі, запишемо так: u_C=u_C’+u_C’’=E+Ae^-(1/RC)t . 3. Одна початкова умова, яку визначають за другим законом комутації для всіх варіантів буде такою: u_C(0_)= u_C(0+)= u_C_;Для моменту часу t = 0+: u_C(0+)= E+A;одержимо сталі інтегрування відповідно до можливих варіантів режиму нескомутованого кола: А = u_C_ - Е.Остаточний розв’язок задачі стосовно напруги на ємності дістанемо, підставивши сталу інтегрування: u_C=E-Ee^-(R/C)t=E(1- e^-(1/RC)t); u_C=E-(E-Uo)e^-(1/RC)t; u_C=E-(E+Uo)e^-(1/RC)t