Перехідні процеси при миттєвій зміні параметрів ділянок ел.кіл

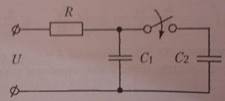
а) Миттєва зміна опору R кола. Розглянемо електричне коло. Розрахуємо струм перехідного процесу за алгоритмом, вважаючи відомими параметри пасивних елементів (R1, R2,L) та вхідну постійну напругу U. 1. До комутації опір R2 був заморочений і через індуктивність проходив струм: i_=U/R1. 2. Струм вимушеного режиму у скомутованому колі буде таким: i’=U/(R1+R2); 3. Характеристичне рівняння і його корені: pL+R1+R2=0 ;p=-(R1+R2)/L. Оскільки розглядається коло першого порядку і характеристичне рівняння має один корінь, вираз вільної складової струму буде: i’’=Ae^pt ; а струм перехідного процесу у загальному вигляді: i=i’+i’’=U/(R1+R2)+Ae ^{–((R1+R2)/L)t} . 4. Сталу інтегрування A розрахуємо виходячи з незалежної початкової умови i(0_)=i(0+)=U/R записаного для моменту часу t=0+: A=U/R1-U/(R1+R2); Підставимо сталу інтегрування й остаточно отримаємо: i=U/(R1+R2)+(U/R1-U/(R1+R2))e ^{–((R1+R2)/L)t} .

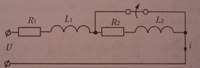
 б) Миттєва зміна індуктивності L кола. Розглянемо електричне коло. Розрахуємо струм перехідного процесу вважаючи відомими параметри пасивних елементів та вхідну постійну напругу U. 1. До комутації опір R2 та індуктивність L2 були заморочені. Через індуктивність L1проходив струм : i1-=U/R1, а в індуктивностіL2 струму не було: i2-=0; 2. Струм вимушеного режиму у скомутованому колі буде i’=U/(R1+R2) ; 3. Характеристичне рівняння і його корені: pL1+pL2+R1+R2=0 ; p=-(R1+R2)/(L1+L2). Оскільки розглядається коло першого порядку і характеристичного рівняння має один корінь, вираз вільної складової струму запишемо так: i’’=Ae^pt, а струм перехідного процесу у загальному вигляді: i=i’+i’’=U/(R1+R2)+Ae ^{–((R1+R2)/(L1+L2))t}; 4. Розрахунок сталої інтегрування з умови незмінності струму гілки в момент комутації тут неможливий, тому що безпосередньо до комутації через індуктивності проходили різні струми, а після комутації струм індуктивностей має бути однаковим, оскільки у цьому режимі обидві індуктивності з’єднані послідовно. Отже, в момент комутації струми індуктивностей змінюються стрибкоподібно, а це призводить до появи на індуктивностях нескінченно великих напруг. Нехтуючи за цих умов скінченними вхідною напругою та спадом напруги на резистивних елементах, рівняння кола для інтервалу комутації (0_<t<0+) на підставі другого закону Кірхгофа запишимо: L1(di1/dt)=-L2(di2/dt); Інтегруємо його в інтервалі комутації: = -  . 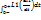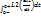Отримуємо: L1(i1(0+)-i1(0+))=-L2(i2(0+)-i2(0_)) ; (i1(0+)-i1(0+))=-L2(i2(0+)-i2(0_) – стрибок струму в момент комутації в кожній з індуктивностей ; L1Δi1(0)=-L2Δi1(0). Розрахунком доводиться, що потокозчеплення кожної індуктивності окремо в момент комутації змінюється, а сумарне потозчеплення гілки залишається незмінним. Це відповідає першому закону комутації. Визначимо початкову умову, урахувавши: а) безпосередньо до комутації струми індуктивностей були такими: i1(0_)=U/Ri2(0_)=0 ; б) безпосередньо після комутації струм індуктивностей будуть однаковими: i1(0+)= i2(0+)= i3(0+) ; (L1+L2)i1(0+)=L1i1(0_)+L2i2(0_)=L1U/R1,звідки i(0+)=U/R * L1/(L1+L2) ; Визначимо сталу інтегрування : U/R * L1/(L1+L2)=U/(R1+R2)+A; Звідки A=U/R1 * L1/(L1+L2) – U/(R1+R2) ; Підставимо сталу інтегрування і остаточно отримаємо : i=U/(R1+R2) + (U/R1 * L1/(L1+L2) – U/(R1+R2)) e ^{–((R1+R2)/(L1+L2))t}