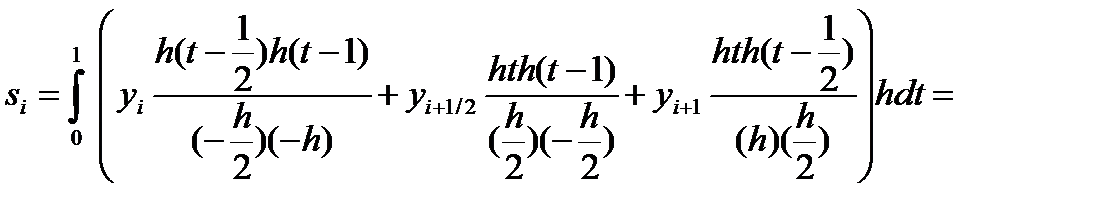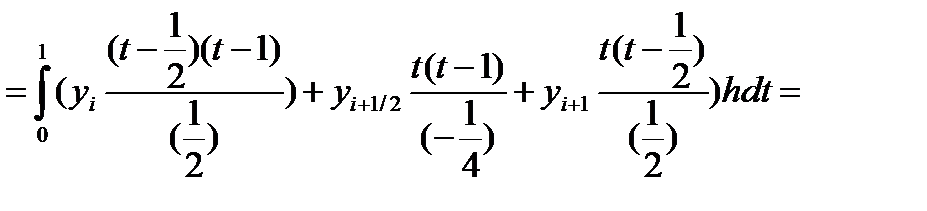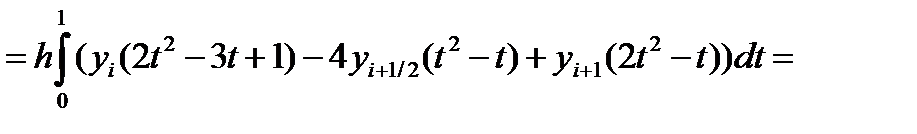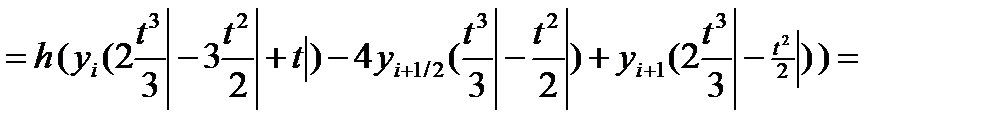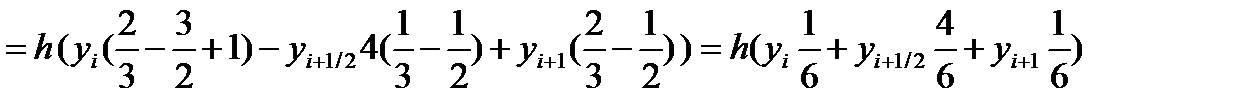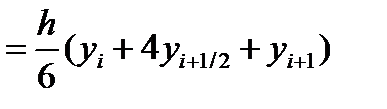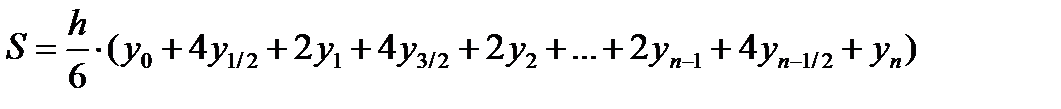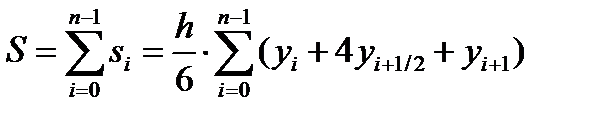Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация. Метод наименьших квадратовСодержание книги
Поиск на нашем сайте Пусть данные некоторого эксперимента представлены в виде таблицы значений независимой переменной x и зависимой переменной y. Требуется отыскать аналитическую зависимость f(x,a0,a1,…,am), являющуюся функцией одной независимой переменной x и параметров a0,a1,a2,…,am, которая наилучшим образом описывала бы эти экспериментальные данные в смысле минимума квадратичного критерия рассогласования R(a0,a1,…,am): Функцию f(x,a0,a1,…,am) определим как полином степени m вида:
или
Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в матричном виде:
При аппроксимации полиномами высших порядков матрица В общем случае количество строк в матрице
Блок-схема аппроксимации.
Интегрирование Пусть на отрезке [a; b] определена непрерывная функция f(x). f=inline(‘<функция>'); Требуется определить значение определенного интеграла
Рис.2.6.1. Интегрирование. Разбиение на равные отрезки. f=inline(‘<функция>'); x=a:h:b; plot(x,f(x),'k-') Площадь S можно вычислить как сумму элементарных площадей определенных для соответствующих элементарных отрезков длиной h: S = s0+s1+s2+…si+…..+sn–1 Произвольную площадь si можно вычислить, как определенный интеграл на отрезке [xi;xi+1] от более простой функции φi(x), которой заменим реальную функцию f(x): Методы прямоугольников. Значение функции φi(x) на отрезке [xi;xi+1] принимается константой Метод прямоугольников вперед. Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как: x=a:h:b-h; S=h*sum(f(x)); Метод прямоугольников назад. Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как: x=a+h:h:b; S=h*sum(f(x)); Метод прямоугольников в среднем. Вычислим x=a+h/2:h:b; S=h*sum(f(x)); Метод трапеций. Функцию φi(x) будем определять как линейную на отрезке [xi;xi+1], т.е. ее график должен проходить через две смежные точки (xi,yi) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по двум точкам (xi,yi) и (xi+1,yi+1):
Метод Симпсона. Определим точку xi+½ = xi+½·h в середине элементарного отрезка [xi;xi+1] и значение функции в этой точке yi+½ Функцию φi(x) будем определять как квадратичную на отрезке [xi;xi+1], т.е. её график должен проходить через три смежные точки (xi,yi),(xi+½ , yi+½) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по трём точкам xi, xi+½ и xi+1:
Тогда значения общей S площади можно вычислить как:
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 40; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.114.190 (0.007 с.) |

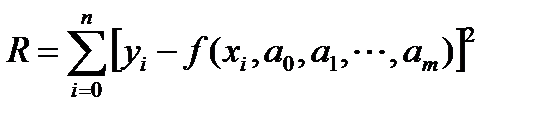
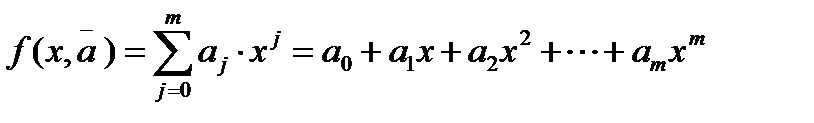 Надо найти такие значения параметров, при которых квадратичный критерий рассогласования имел бы минимальное значение
Надо найти такие значения параметров, при которых квадратичный критерий рассогласования имел бы минимальное значение 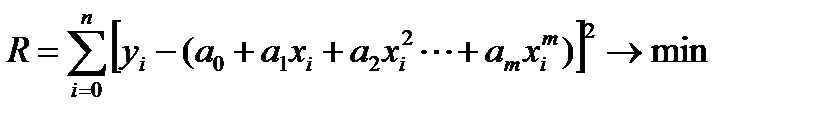 Вывод формулы для определения параметров в матричном виде рассмотрим на примере полинома второй степени (m=2).
Вывод формулы для определения параметров в матричном виде рассмотрим на примере полинома второй степени (m=2). 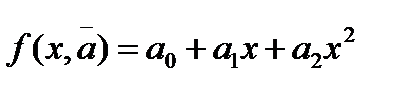 Тогда критерий R будет являться функцией трёх переменных a0, a1, a2:
Тогда критерий R будет являться функцией трёх переменных a0, a1, a2: 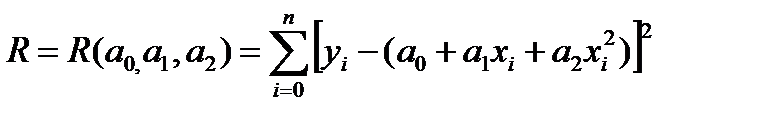 Необходимые условия минимума критерия R имеют вид:
Необходимые условия минимума критерия R имеют вид: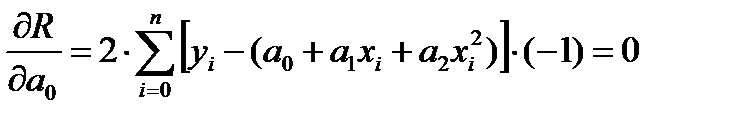
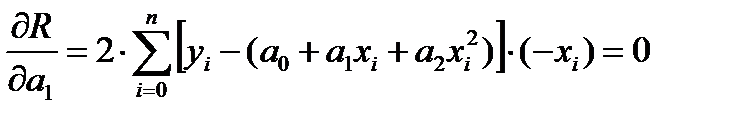
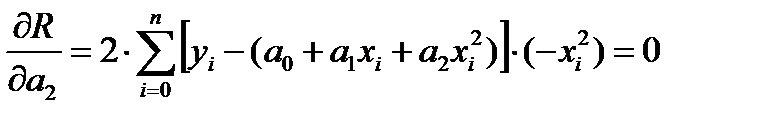
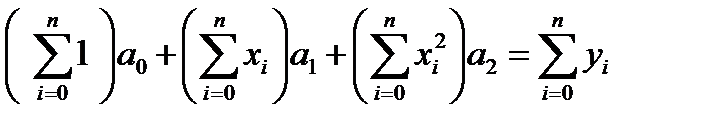
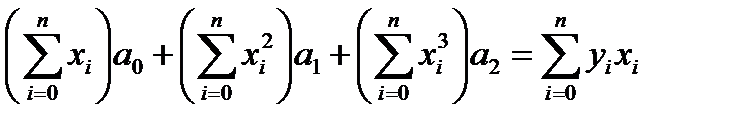
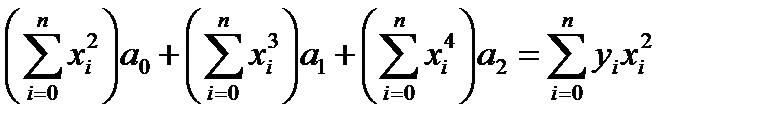
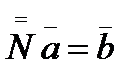 где
где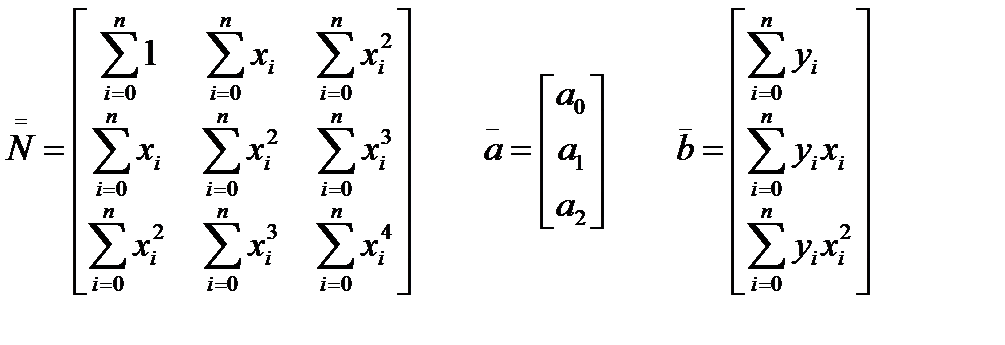 Для удобства формирования матрицы коэффициентов
Для удобства формирования матрицы коэффициентов 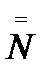 и столбца свободных членов
и столбца свободных членов 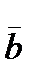 введем матрицу
введем матрицу 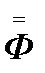 элементы которой определяются через значения независимой переменной xi, i=0,1,2,…,n
элементы которой определяются через значения независимой переменной xi, i=0,1,2,…,n 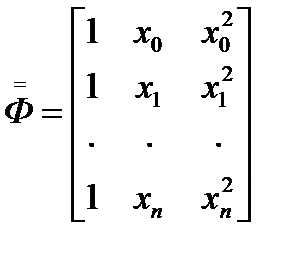 тогда
тогда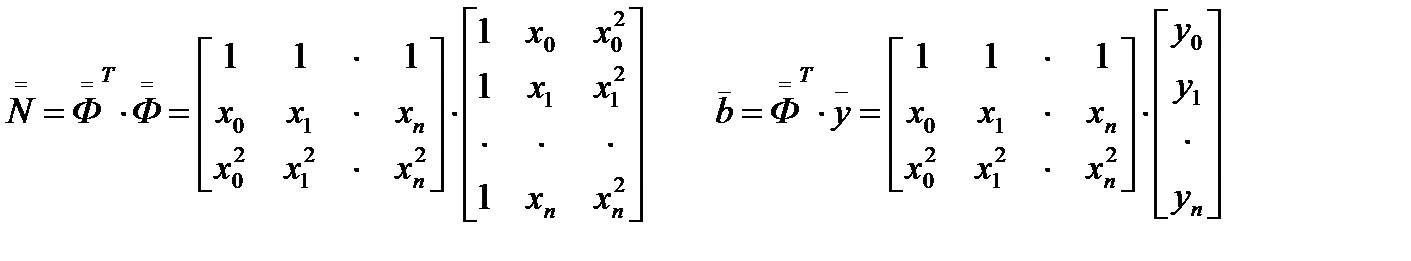
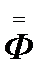 будет иметь вид:
будет иметь вид: 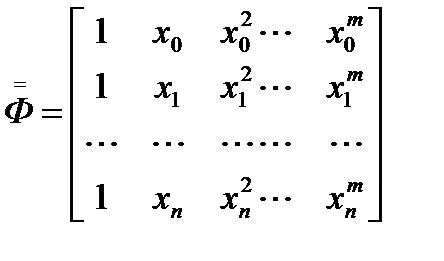
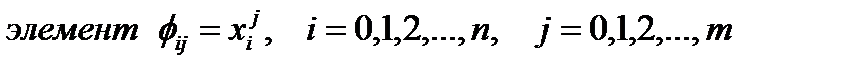
 равно количеству точек, а количество столбцов равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру.
равно количеству точек, а количество столбцов равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру. 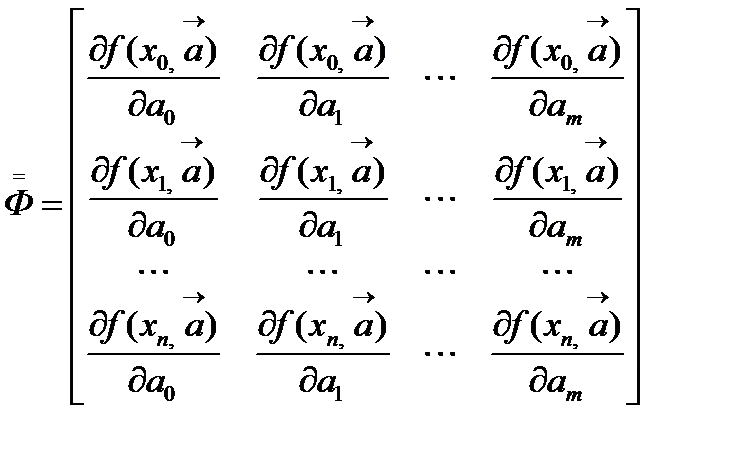
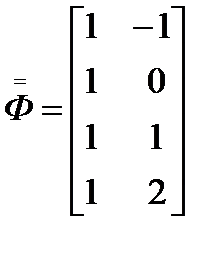
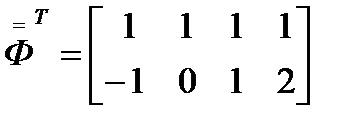
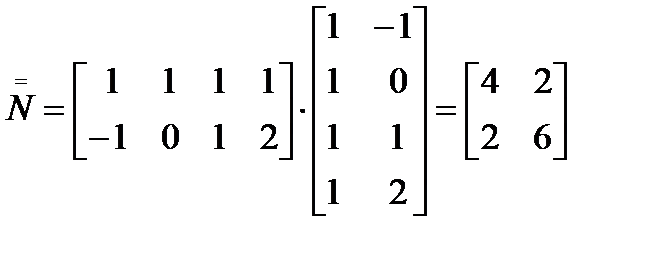
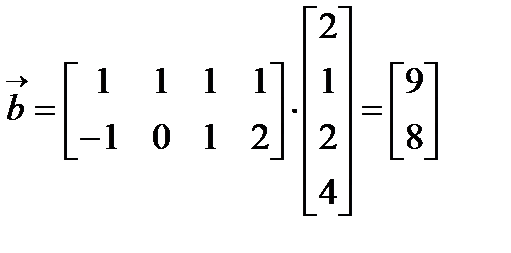
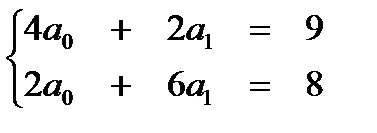
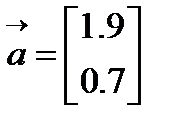
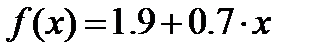
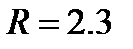
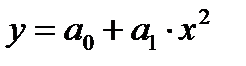
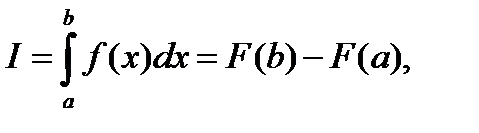 которое числено равно площади S фигуры, ограниченной графиком функции f(x) и осью x, на заданном отрезке [a; b]. Для приближенного вычисления площади, разобьем отрезок [a; b] на n равных элементарных отрезков точками: x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b,
которое числено равно площади S фигуры, ограниченной графиком функции f(x) и осью x, на заданном отрезке [a; b]. Для приближенного вычисления площади, разобьем отрезок [a; b] на n равных элементарных отрезков точками: x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b, 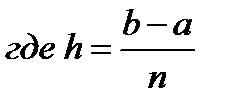 – шаг разбиения. Значение функции f(x) в точках (рис.2.6.1) разбиения xi обозначим через yi.
– шаг разбиения. Значение функции f(x) в точках (рис.2.6.1) разбиения xi обозначим через yi.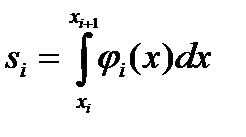 Вид функции φi(x) будет определять название метода.
Вид функции φi(x) будет определять название метода.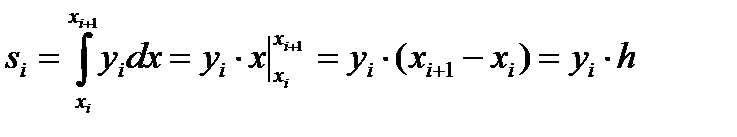 , тогда
, тогда 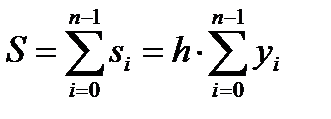
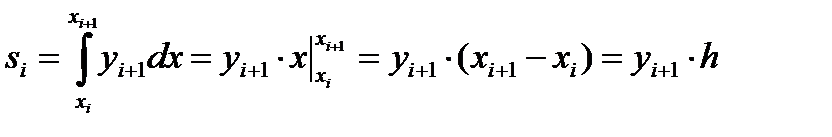 , тогда
, тогда 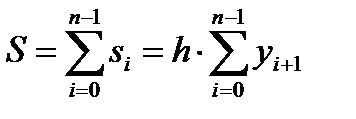
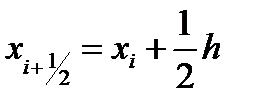 и значение функции
и значение функции 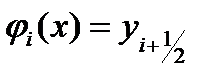 Тогда значения элементарной si и общей S площади можно вычислить как
Тогда значения элементарной si и общей S площади можно вычислить как 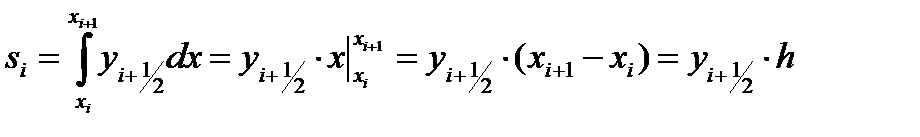
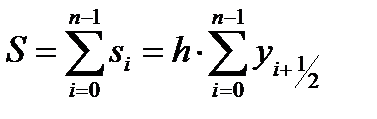
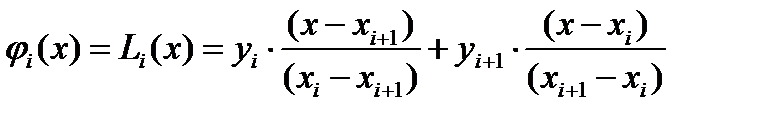 тогда значения элементарной si площади можно вычислить как:
тогда значения элементарной si площади можно вычислить как: 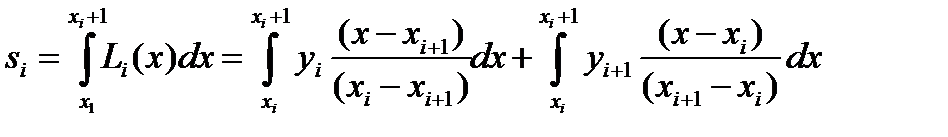 Введем переменную
Введем переменную 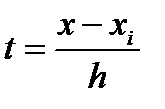 Тогда x = xi + h·t и dx = h·dt. Значениям x, равным x, xi+1 соответствуют значения t, равные 0, 1. Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1). Элементарную площадь si с использованием новой переменной определим как:
Тогда x = xi + h·t и dx = h·dt. Значениям x, равным x, xi+1 соответствуют значения t, равные 0, 1. Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1). Элементарную площадь si с использованием новой переменной определим как: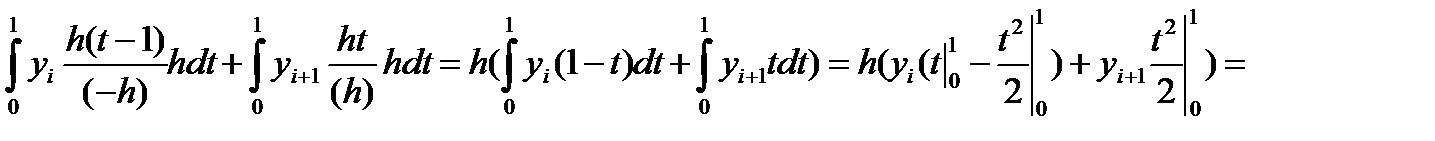
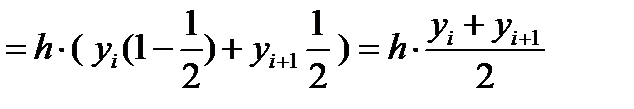
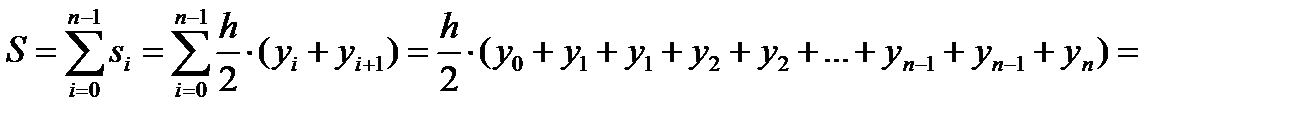
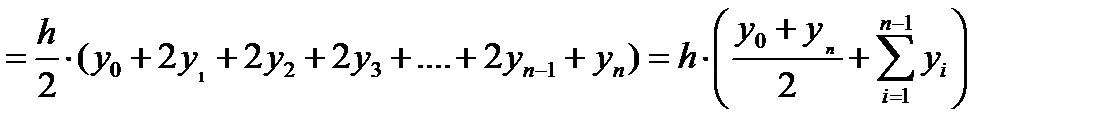
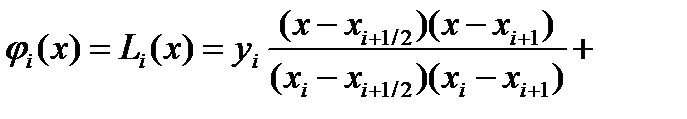
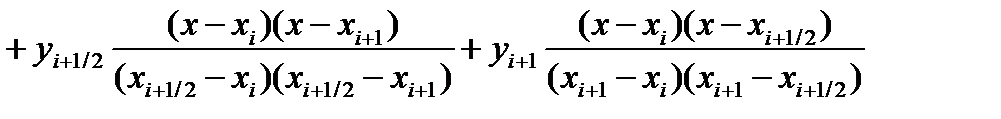 Тогда значения элементарной si площади можно вычислить как:
Тогда значения элементарной si площади можно вычислить как: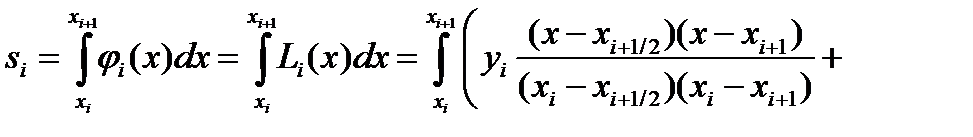
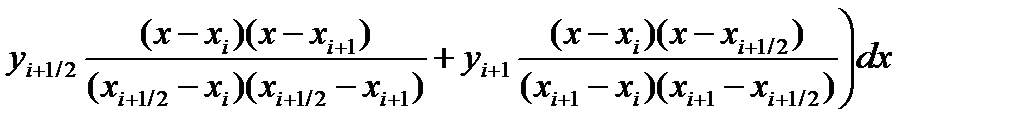 Введем переменную
Введем переменную 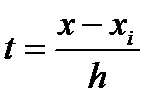 тогда x = xi + h·t и dx = h·dt. Значениям x, равным xi, xi+½, xi+1 соответствуют значения t, равные 0,½,1 Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+½) = xi – xi+½ + h·t = h(t- ½) Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1) Элементарную площадь si с использование новой переменной определим как:
тогда x = xi + h·t и dx = h·dt. Значениям x, равным xi, xi+½, xi+1 соответствуют значения t, равные 0,½,1 Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+½) = xi – xi+½ + h·t = h(t- ½) Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1) Элементарную площадь si с использование новой переменной определим как: