Методы одномерной оптимизации

Дана некоторая функция f(x) от одной переменной x, надо определить такое значение x*, при котором функция f(x) принимает экстремальное значение. Под ним обычно понимают минимальное или максимальное значения. В общем случае функция может иметь одну или несколько экстремальных точек.

Нахождение этих точек с заданной точностью можно разбить на два этапа. Сначала экстремальные точки отделяют, т.е. определяются отрезки, которые содержат по одной экстремальной точке, а затем уточняют до требуемой точности e. Отделение можно осуществить, как графически, так и табулированием.

Все методы уточнения точек экстремумов будем рассматривать относительно уточнения минимума на заданном отрезке.

 

Метод деления на три равных отрезка.

1) Дан отрезок [a;b] на котором определена функция f(x) и точность e. Надо уточнить точку минимума с заданной точностью. Введём новое обозначение точек x₁=a и x₄=b. Вычислим Z=1/3.

2) Делим отрезок на три равные части и определяем точку x₂=x₁+Z(x₄-x₁) и точку x₃=x₄-Z(x₄-x₁). Вычисляем значения функции в этих точках F2=f(x₂) F3=f(x₃).

3) Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x1=x1, а x₄=x₃, иначе x₁=x₂, а x₄=x₄.

4) Проверяем условие окончания итерационного процесса | x₄-x₁ | £ 2e. Если оно выполняется, то определим решение, как x=(x₄+x₁)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 2.

 

Введем понятие эффективности, как отношение доли сокращения отрезка к количеству вычисления функции на одной итерации тогда Q=0,33/2≈0,17

 

Блок-схема метода деления на три равных отрезка.

начало F2<F3 x, f(x) a, b, ε || f(x). x1 := a; x4:=b: Z=1/3 x1:=x2 x4:=x3 x2:=x1+Z(x4-x1); x3:=x4-Z(x4-x1) F2:=f(x2); F3:=f(x3) |x4-x1|£2ε конец x:=(x1+x4)/2 нет да

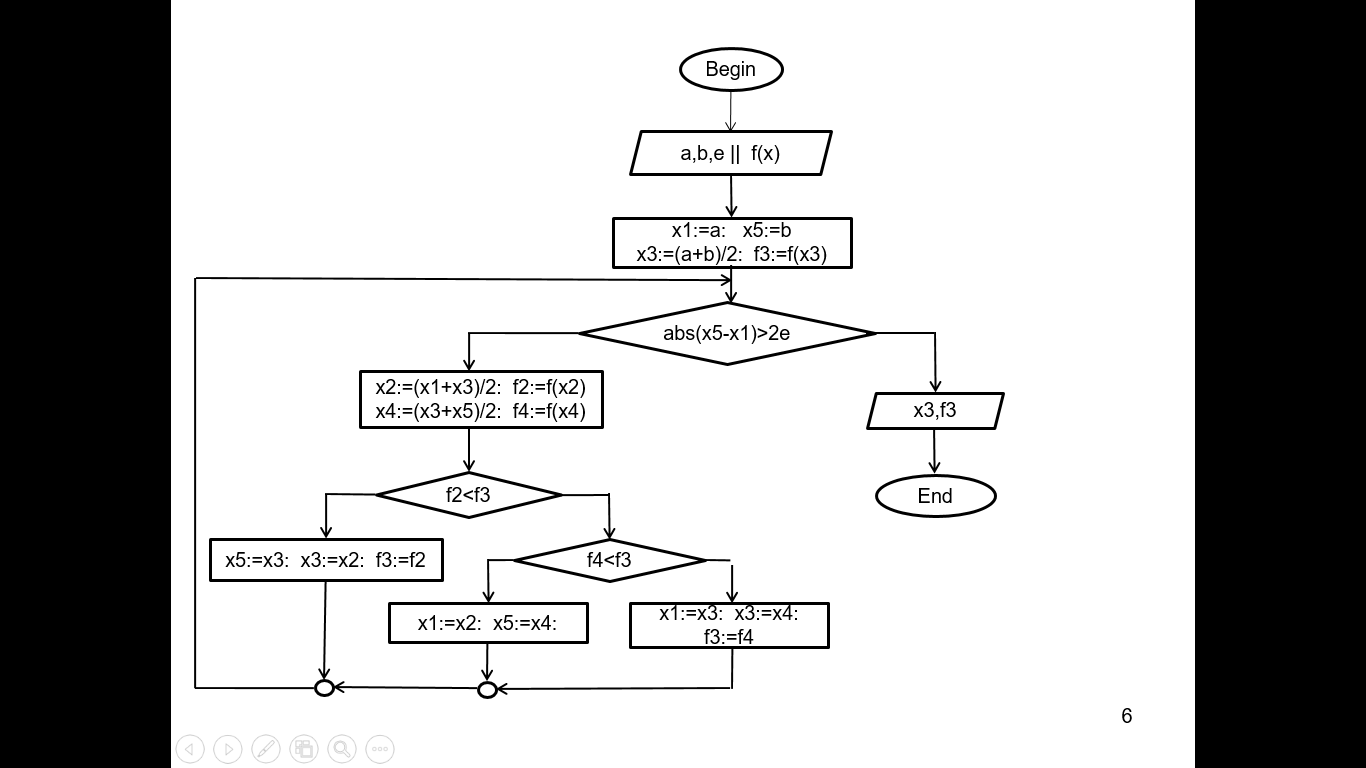
Попробуем увеличить долю сокращения отрезка. Метод деления отрезка пополам.

1) Дан отрезок [a;b] на котором определена функция f(x) и точность e. Надо уточнить точку минимума с заданной точностью. Введём новое обозначение точек x₁=a и x₅=b. Делим отрезок [x_1;x₅] пополам и определяем точку середины x₃=(x₅+x₁)/2 и значение функции F3=f(x ₃).

2) Делим отрезок [x_1;x₃] пополам и определяем точку середины x₂=(x₁+x₃)/2 и значение функции F2=f(x₂). Делим отрезок [x_3;x₅] пополам и определяем точку середины x₄=(x₃+x₅)/2 и значение функции F4=f(x₄). 

3) Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как: x₁=x₁, x₅=x₃, x₃=x₂ и F3=F2 иначе если F4<F3, то x₁=x₃, x₅=x₅, x₃=x₄ и F3=F4 иначе x₁=x₂, x₅=x₄. Проверяем условие окончания итерационного процесса | x₅-x₁ | £ 2e. Если оно выполняется, то определим решение, как x=x₃ и значение функции в этой точке f(x). Иначе перейдем на пункт 2. Эффективность метода Q≈0,5/2=0,25

Блок-схема. Одномерная оптимизация. Деление на два равных отрезка

Попробуем разбивать отрезок (рис.2.9.1) на такие части, чтобы одну из двух точек и соответствующее значение функции мы могли использовать на следующей итерации. Метод Золотого сечения.

 

D D d d L x1  x2  x3  x4  x4  x3  x2  x1

 

 

Рис.2.9.1. Разбиение отрезка так, чтобы использовать одну из точек затем еще раз.

 

делим на  Заменяем

Решая получим

Алгоритм.

1) Дан отрезок [a;b] на котором определена функция f(x) и точность e. Надо уточнить точку минимума с заданной точностью. Введём новое обозначение точек x₁=a и x₄=b и вычислим Z=(3-√5)/2.

2) Делим отрезок на три части и определяем точку x₂=x₁+Z(x₄-x₁) и точку x₃=x₄-Z(x₄-x₁). Вычисляем значения функции в этих точках F2=f(x₂) F3=f(x₃).

3) Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x₁=x₁, x₄=x₃ , x₃=x₂, F3=F2 x₂=x₁+z(x₄-x₁) F2=f(x₂) иначе x₁=x₂, x₄=x₄, x₂=x₃ F2=F3 x₃=x₄-z(x₄-x₁)
F3= f(x₃).

4) Проверяем условие окончания итерационного процесса | x₄-x₁ | £ 2e. Если оно выполняется, то определим решение, как x=(x₄+x₁)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 3.

Эффективность, как отношение доли сокращения отрезка к количеству вычисления функции на одной итерации: Q=0,3819/1≈0,3819