
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы многомерной оптимизации
Дана некоторая функция многих переменных f(x1,x2,x3,…..,xn) или Для удобства графической иллюстрации методов определим представление функции в виде линий уровня. Дана целевая функция Проведем сечения поверхности равно отстоящими плоскостями, которые параллельны плоскости изменения переменных x1 и x2. Линии этих сечений проецируем на плоскость изменения переменных. Получим концентрические окружности. Эти линии называются линиями уровня или линиями постоянных значений. Основная характеристика любой из линий это то, что в любой точке этой линии значение функции постоянно. Рассечем заданную поверхность функции тремя плоскостями по уровням. Определим зависимости x1 от x2 для соответствующих линий уровней. Для заданной функции f(x1,x2) линии уровней будут представлять окружности с соответствующими радиусами:
Рис. 2.10.1. Трехмерная фигура – параболоид вращения.
Рис. 2.10.2. Сечения фигуры – параболоида вращения.
Функция Химмельблау
Рис. 2.10.3. Функция Химмельблау.
fxx01=inline('(x1.^2+x2-11).^2+(x1+x2.^2-7).^2') [x1,x2]=meshgrid(-4:0.05:4); z=fxx01(x1,x2); contour(x1,x2,z)
Все методы многомерной оптимизации делятся на два класса: градиентные; безградиентные.
Градиентный метод. Градиентом называется вектор равный сумме произведений частных производных на соответствующие орты. Орта – единичный связанный вектор, направленный вдоль координатной оси.
Рис. 2.10.4. Градиент, антиградиент и касательная.
Алгоритм 1) Дана функция n переменных 2) Вычисляем вектор градиента 3) Вычисляем новое приближение, делая шаг в направление антиградиента 4) Проверяем условие Fz < Fx 5) Если условие выполняется, то за начальное приближение принимаем 6) Иначе, проверяем условие окончания h < ε 7) Если условие выполняется, то выводим 8) Если не выполняется, то уменьшаем параметр шага h=h/3 и переходим на пункт 2
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 34; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.209 (0.007 с.) |
 надо найти такое значение
надо найти такое значение  при котором функция
при котором функция  принимает экстремальное значение (минимальное или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией.
принимает экстремальное значение (минимальное или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией. 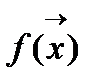 называют оптимизируемой или целевой функцией
называют оптимизируемой или целевой функцией  называют вектором параметров оптимизации. В области определения функции может быть несколько экстремумов. Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов. Какой именно экстремум будет определён, зависит от выбора начального приближения:
называют вектором параметров оптимизации. В области определения функции может быть несколько экстремумов. Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов. Какой именно экстремум будет определён, зависит от выбора начального приближения:  Методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных.
Методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных. которая графически представляет собой поверхность параболоида вращения.
которая графически представляет собой поверхность параболоида вращения.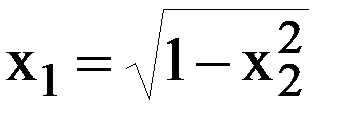
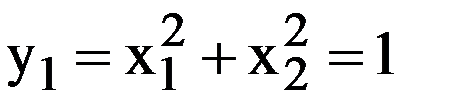 R1=√1=1;
R1=√1=1; 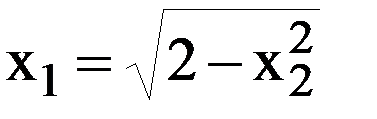
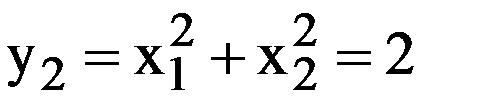 R2=√2=1.41;
R2=√2=1.41; 
 R3=√3=1.73;
R3=√3=1.73;

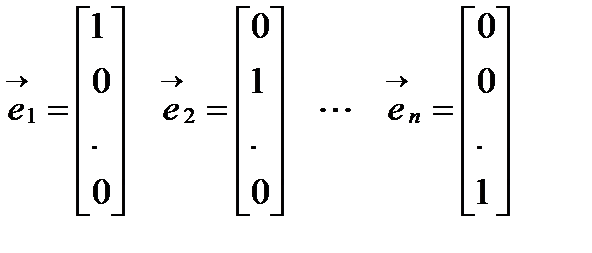
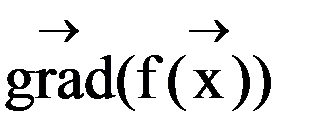
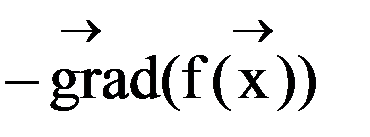
 Основные свойства градиента: Норма градиента определяет скорость изменения функции в направление градиента; Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна; Градиент перпендикулярен линии уровня. Антиградиентом называется вектор, направленный в сторону противоположную градиенту.
Основные свойства градиента: Норма градиента определяет скорость изменения функции в направление градиента; Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна; Градиент перпендикулярен линии уровня. Антиградиентом называется вектор, направленный в сторону противоположную градиенту.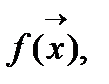 точность ε, параметр шага h, задаем начальное приближение
точность ε, параметр шага h, задаем начальное приближение  вычисляем значение функции
вычисляем значение функции 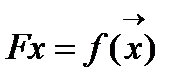
 и единичный вектор градиента
и единичный вектор градиента 
 и вычисляем значение функции
и вычисляем значение функции 
 т.е.
т.е.  , переходим на пункт 2.
, переходим на пункт 2. Конец алгоритма
Конец алгоритма


