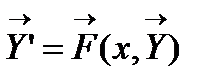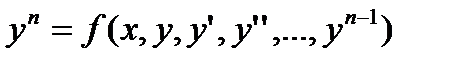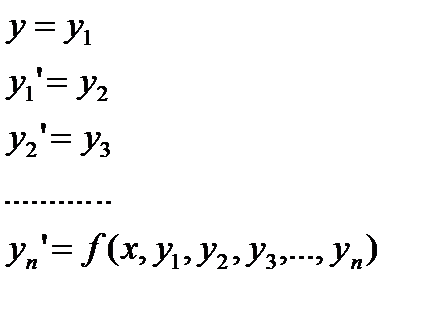Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения обыкновенных дифференциальных уравненийСодержание книги
Поиск на нашем сайте Общий вид обыкновенного дифференциального уравнения, устанавливающего связь между независимой переменной x неизвестной функцией y и ее производными y’,y”,…,y(n), может мыть представлен следующим образом: Порядок наивысшей производной, входящей в уравнение, называется порядком этого уравнения. Решение дифференциального уравнения (интегрированием) является некоторая функциональная зависимость y=y(x), которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения записывается в виде: y=y(x,c1,c2,…,cn), где c1,c2,…,cn произвольные постоянные. Решение, полученное из общего решения при фиксированных значениях, называется частным решением уравнения. Постоянные c1,c2,…,cn можно определить, задав n условий. Если эти условия заданы как совокупность значений искомой функции и всех ее производных до (n-1) порядка включительно в некоторой точке x0, то задача решения уравнения называется задачей Коши, а заданные условия: y(x0)=y0, y’(x0)=y’0, y”(x0)=y”0,…, yn-1(x0)=yn-10 называются начальными условия. Если же условия заданы при нескольких значениях x, то задача решения дифференциального уравнения будет называться граничной или краевой задачей. Рассмотрим дифференциальное уравнение первого порядка: Последнее уравнение называется дифференциальным уравнением, разрешенным относительно производной. Значение производной равно тангенсу угла наклона касательной к графику функции в точке (x,y). Функцию f(x,y) будем называть правой частью дифференциального уравнения. Общим решением уравнения будет являться семейство функций y=y(x,c1) различающихся значение постоянной c1. Задаем одно начальное условие y(x0)=y0, которое определяет значение c1и конкретное частное решение – задача Коши. Для простейшего дифференциального уравнения y’=3x2. Общее решение имеет вид y=x3+c, а подставив в общее решение начальное условие x0=1, y0=2 вычислим с=1 и определим частное решение как: y=x3+1 Метод Эйлера. Дано дифференциальное уравнение y’=f(x,y), удовлетворяющее начальному условию y(x0)=y0. Требуется найти решение на отрезке [a,b]. Разобьем (рис.2.11.1) отрезок интегрирования на n равных частей: x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b, тогда величина шага интегрирования будет равна:
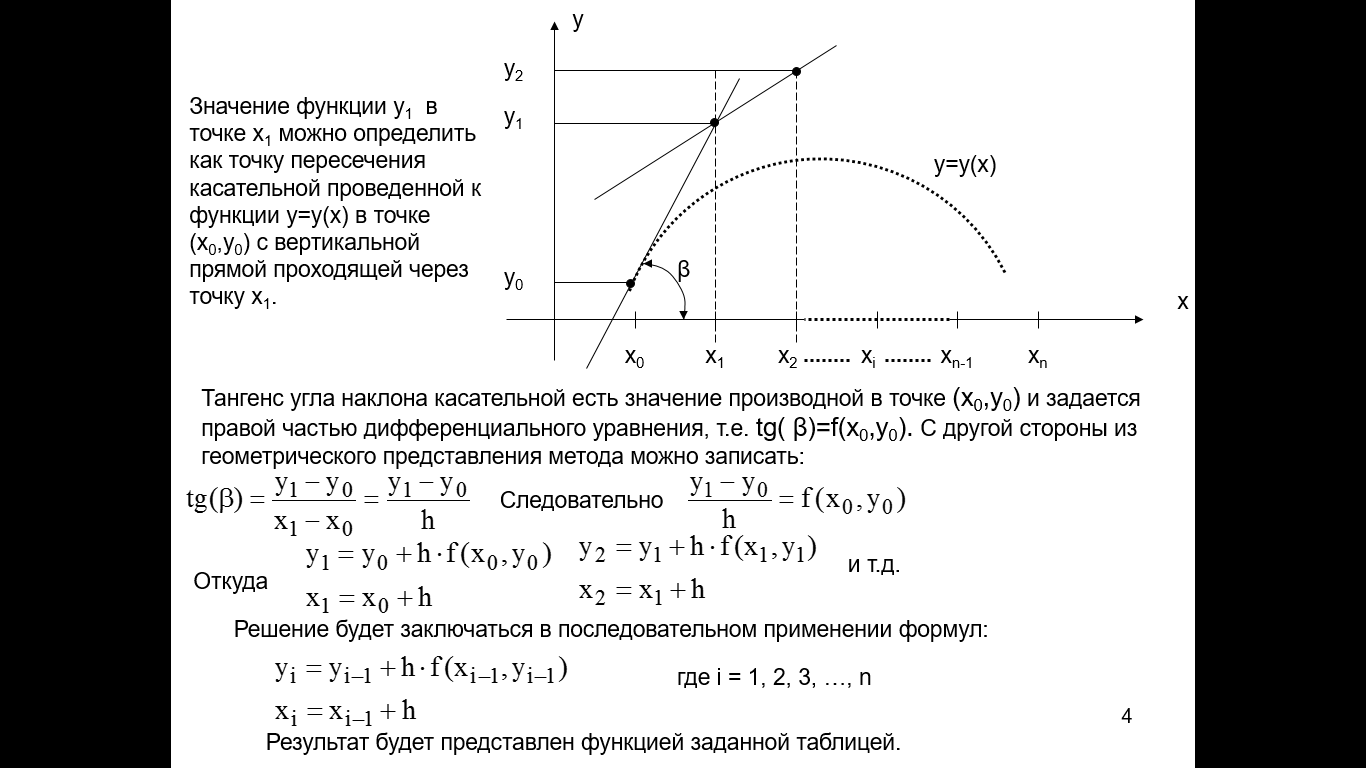
Рис.2.11.1. Метод Эйлера. Значение функции y1 в точке x1 можно определить как точку пересечения касательной проведенной к функции y=y(x) в точке (x0,y0) с вертикальной прямой проходящей через точку x1. Тангенс угла наклона касательной есть значение производной в точке (x0,y0) и задается правой частью дифференциального уравнения, т.е. tg(β)=f(x0,y0). С другой стороны из геометрического представления метода можно записать: Модифицированный метод Эйлера. Графическая интерпретация. Определяем (рис.2.11.2) точку
Рис.2.11.2. Модифицированный метод Эйлера.
произвольную точку определим
Система дифференциальных уравнений Обозначив Решением системы называется вектор-функция Дифференциальные уравнения n-ого порядка Приводим к системе дифференциальных уравнений
|
||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

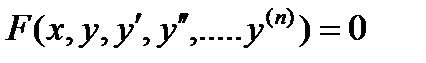
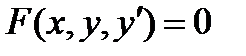 соотношение часто удается записать в виде:
соотношение часто удается записать в виде: 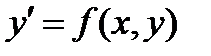
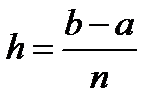
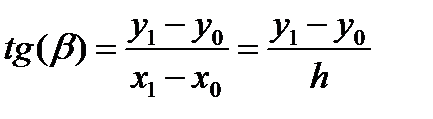 Следовательно
Следовательно 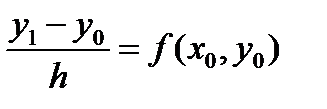 Откуда
Откуда 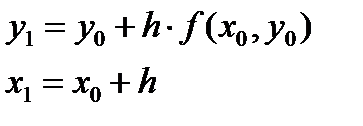 тогда
тогда 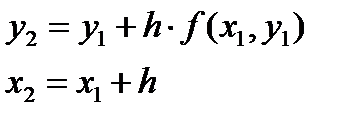 и так далее. Решение будет заключаться в последовательном применении формул:
и так далее. Решение будет заключаться в последовательном применении формул: 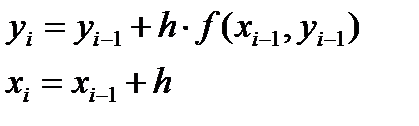 где i = 1, 2, 3, …, n Результат будет представлен функцией заданной таблицей.
где i = 1, 2, 3, …, n Результат будет представлен функцией заданной таблицей.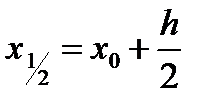 и вычисляем значение функции в этой точке
и вычисляем значение функции в этой точке 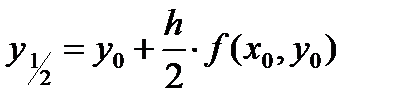 Значение функции y1 в точке x1 определяем, как точку пересечения касательной, вычисленной в точке (x1/2,y1/2) и проведенной к функции y=y(x) в точке (x0,y0), с вертикальной прямой проходящей через точку x1.
Значение функции y1 в точке x1 определяем, как точку пересечения касательной, вычисленной в точке (x1/2,y1/2) и проведенной к функции y=y(x) в точке (x0,y0), с вертикальной прямой проходящей через точку x1.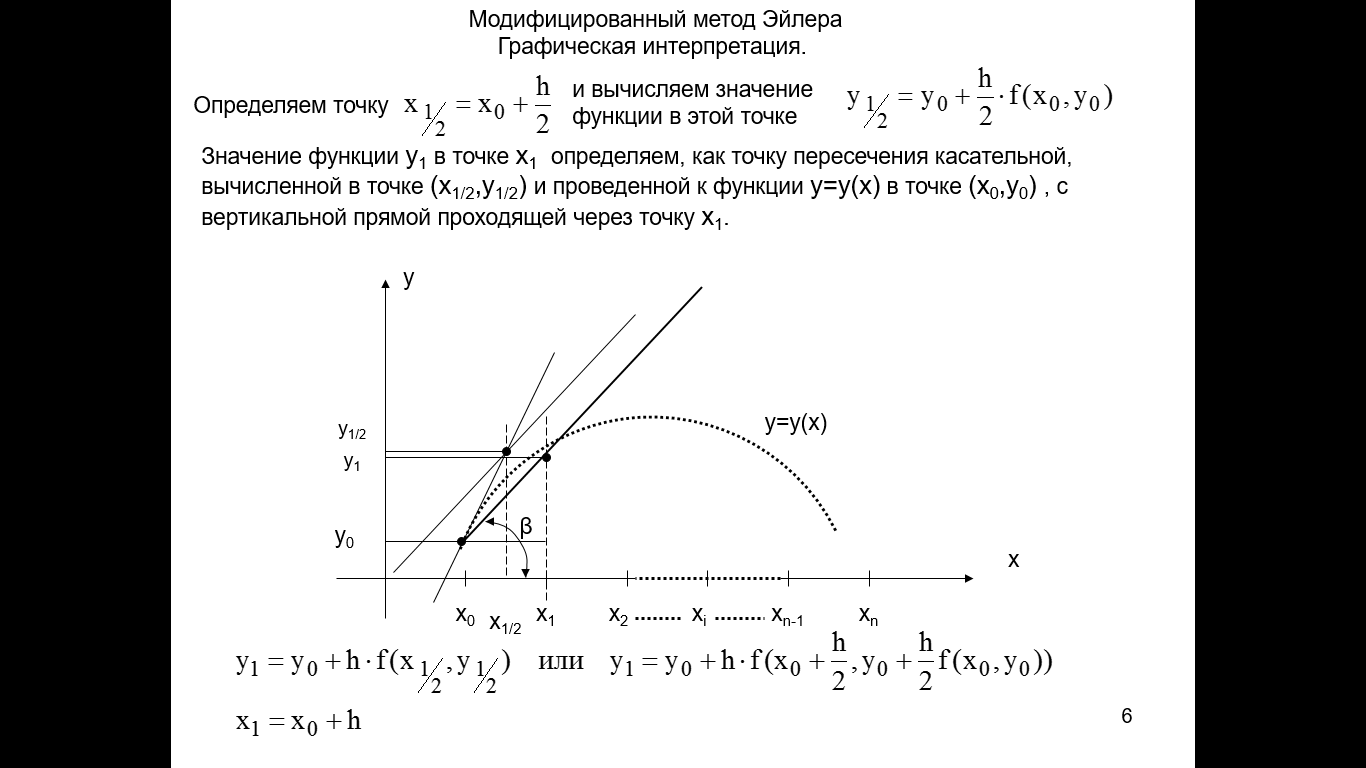
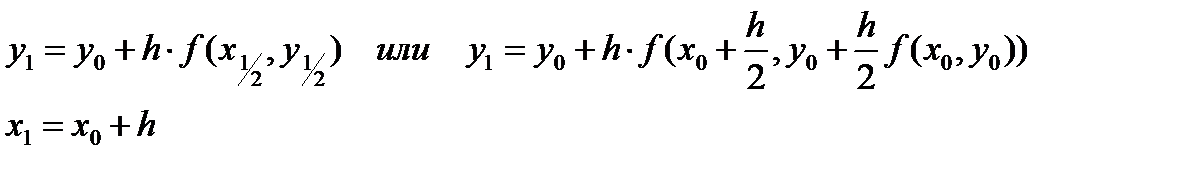
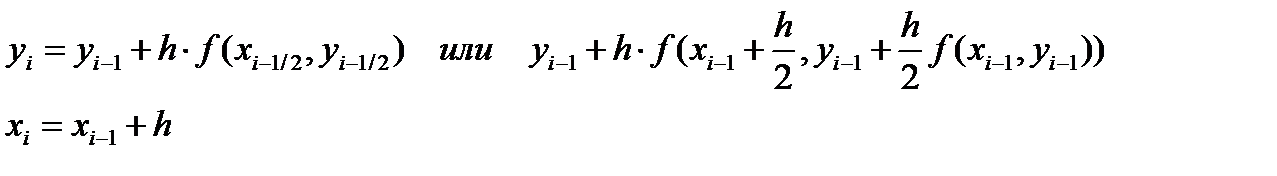
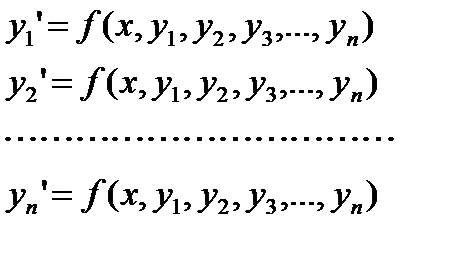 где x — независимая переменная, а y 1(x), y 2(x),..., yn (x) — неизвестные функции, n — порядок системы.
где x — независимая переменная, а y 1(x), y 2(x),..., yn (x) — неизвестные функции, n — порядок системы.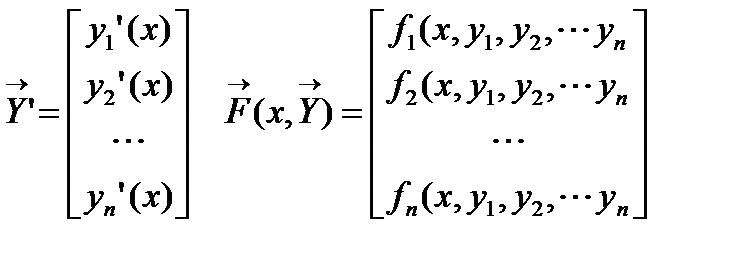 или
или 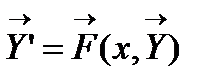
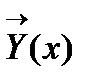 , которая определена и непрерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех
, которая определена и непрерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех 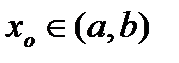 справедливо
справедливо