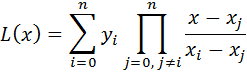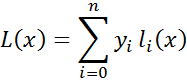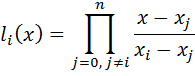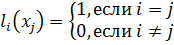Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статобработка с использованием критерия СтьюдентаСодержание книги
Поиск на нашем сайте
Если Uрасч > Up,f, то подозреваемое значение с вероятностью b является грубой шибкой. Грубая ошибка исключается из серии. Критерий Up,f определяется из табл. 2.4.1 при уровне значимости p = 1 – b и числе степеней свободы f = n – 2.
Табл. 2.4.1. Up , f определяется при p = 1 – b и f = n – 2.
Критерий Стьюдента определяется из табл. 2.4.2 при р = 1 – b и f = n – 1.
Табл. 2.4.2. Критерий Стьюдента определяется при р = 1 – b и f = n – 1.
Пример: p = 0.05 b = 0.95 n = 6
y среднее= 39.16/6 = 6.527 дисперсия S2y = 0.0659
Uтаб для f = 6-2 = 4 p = 0.05 имеет значение 1.996 Подозреваемое значение y4= 7.02 т.к. |7.02-6.527|=0.493 максимальна
2.105>1.996 поэтому х4= 7.02 является грубой ошибкой и удаляется из серии n = 5
y среднее= 32.14 / 5 = 6.428 дисперсия S2y = 0.0094 Uтаб для f = 5-2 = 3 p = 0.05 имеет значение 1.869 Подозреваемое значение x1 = 6.28 т.к. |6.28 -6.428|=0.148 максимальна
Uрасч= 1.709 <1.869 поэтому y1 = 6.28 не является грубой ошибкой Для последней серии строим доверительный интервал tтаб0.05, 4 = 2.78
6.308 < y* < 6.548
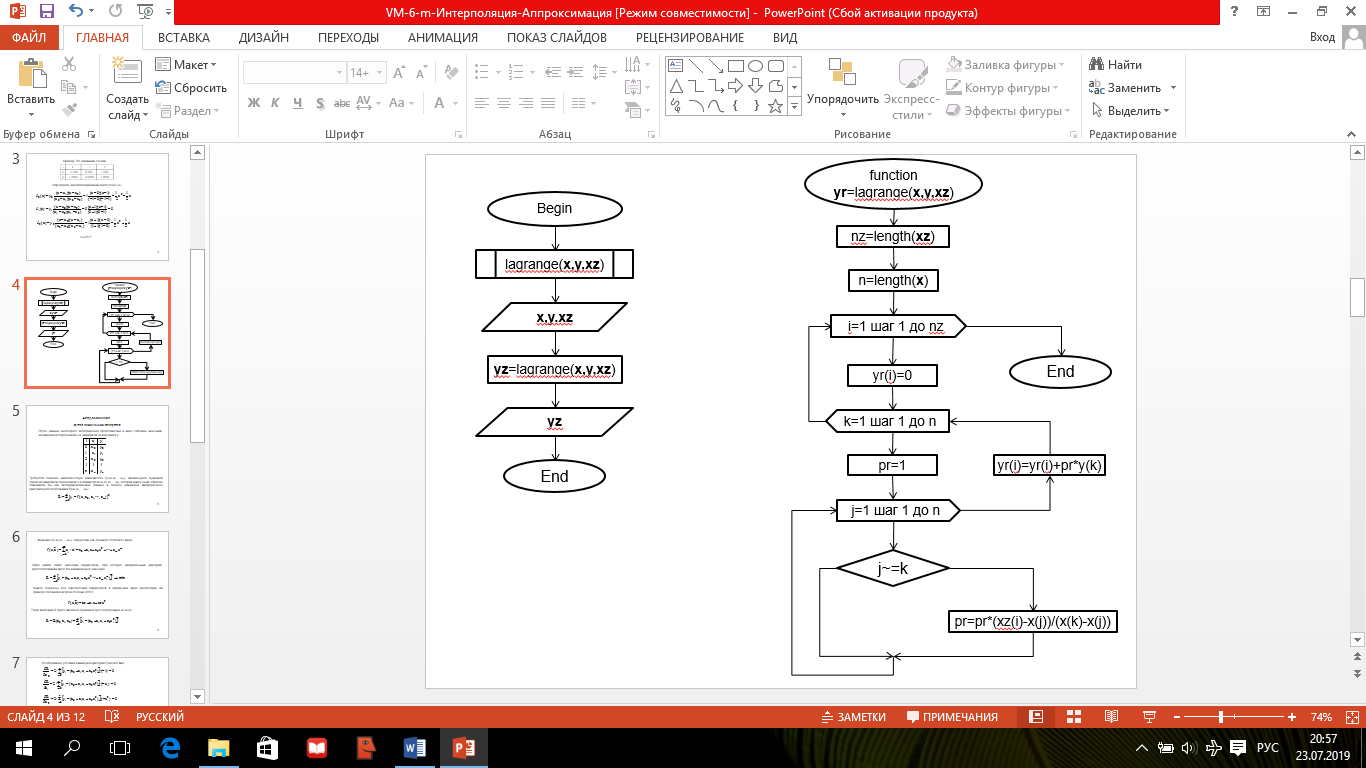
Приближение функции. Интерполяция. Аппроксимация Для заданных значениях независимой переменной xi и соответствующих им значениях зависимой переменной yi (i=0,1,2,…,n) определить аналитическую зависимость. y=f(x) Основные этапы при приближение функции: Выбор вида зависимости; Выбор критерия; Выбор узловых точек; Оценка точности. Интерполяция (определение аналитической зависимости функции между x и y в виде некоторой функции f(x), которая в узловых точках принимает заданные значения f(xi)=yi, где i=0,1,2,…,n) используется для замены реальной сложной функции более простой на небольшом интервале области определения функции, а также для вычислений промежуточных значений функции заданной таблично. Метод с использованием многочлена Лагранжа. Пусть в n+1 узловой точке x0, x1, x2, …, xn определены значения y0, y1, y2, …, yn. Требуется построить многочлен L(x) степени не выше n, который принимает в узловых точках заданные значения, т.е. L(x0)=y0, L(x1)=y1, L(x2)=y2, …, L(xn)=yn. Рассмотрим многочлен вида где i = 0,1,2,3,…….,n, который только в точке xi принимает значение yi, а в остальных равен нулю. из этого условия можно определить ci: Многочлен, который в n+1 узловой точке будет принимать заданные значения, можно представить как сумму многочленов вида (2). Блок-схема интерполяции многочленом Лагранжа
Пример. По заданным точкам: xi=-1 0 1; yi=1 0 1. Определить интерполяционный многочлен L(x).
L(x)=x2
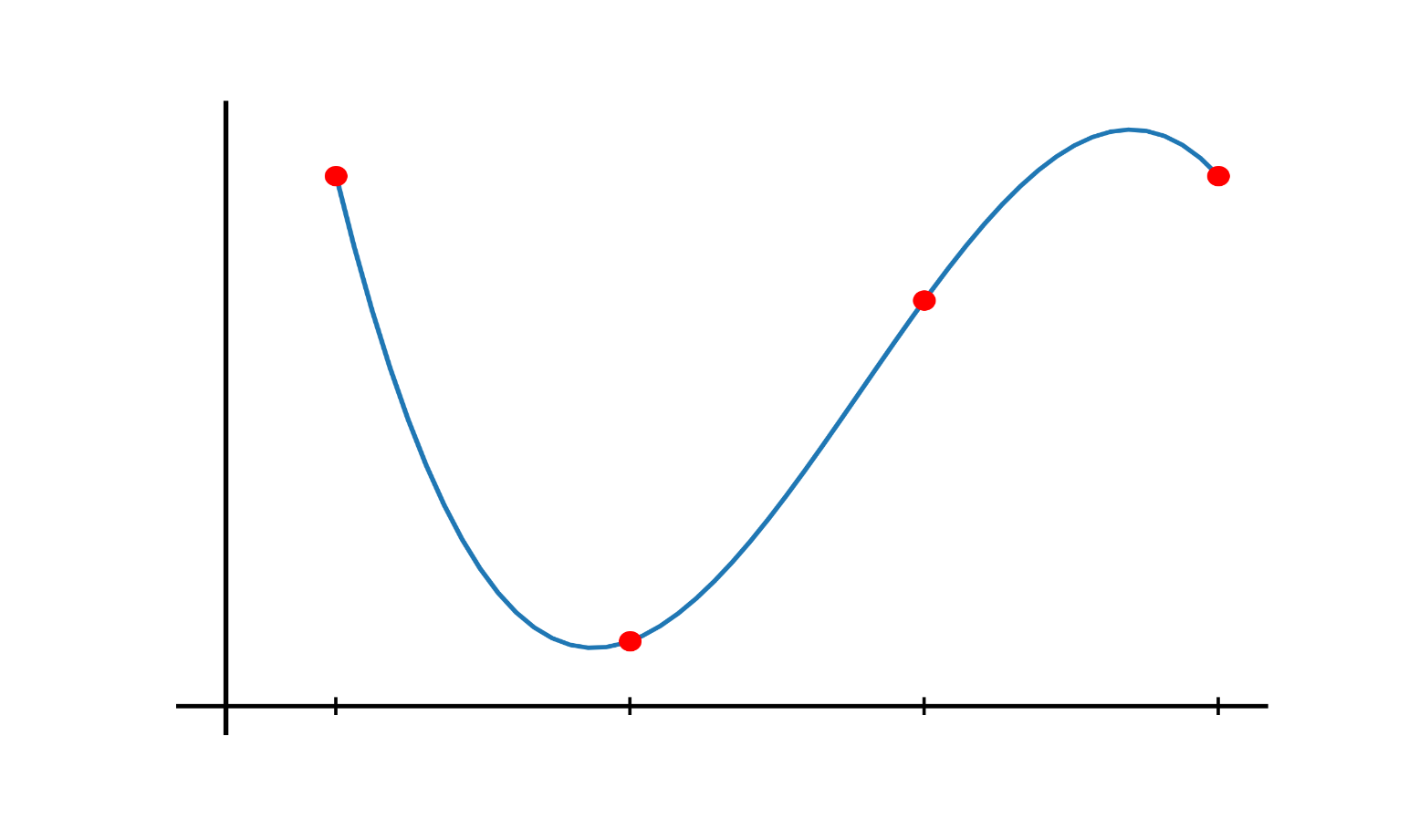
Рис. 2.5.1. Интерполяция
Определение Пусть функция
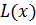 степени не выше степени не выше 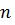 такой, что такой, что 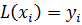
ниже на рисунке показаны графики li (x), а также график L (x)
Рис. 2.5.2. Интерполяция, графики всех функций
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |




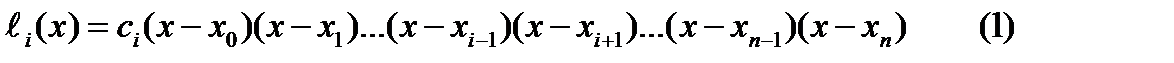
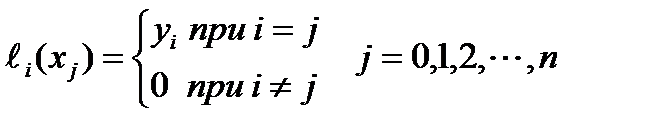

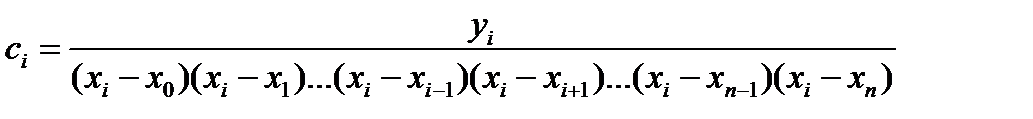 и тогда многочлен (1) примет вид:
и тогда многочлен (1) примет вид: 
 или
или 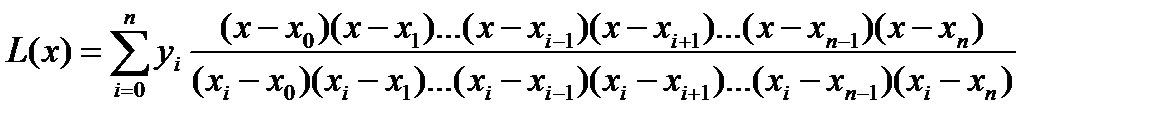


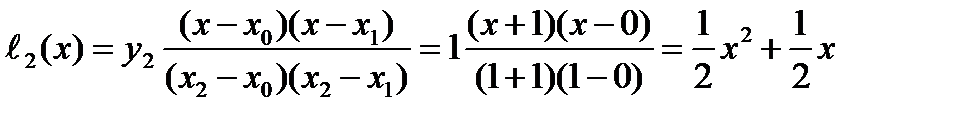
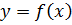 задана в
задана в 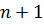 точках
точках