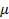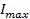Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт среднего значения горизонтальной составляющей магнитного поля ЗемлиСодержание книги
Поиск на нашем сайте
Пример расчёта отклонения от среднего для каждого из значений индукции поля Земли
Расчет суммы квадратов отклонений от среднего значения
Расчёт случайной погрешности по формуле Стьюдента (коэффициент Стьюдента
Расчёт абсолютной приборной погрешности косвенного измерения
Расчёт полной абсолютной погрешности
Расчёт относительной погрешности измерения
Выводы по работе:
Контрольные вопросы и место для ответов 1. Что такое магнитное поле? Что является источниками магнитного поля?
2. Какие характеристики магнитного поля Вы знаете?
3. Что такое силовая линия магнитного поля?
4. В чём выражается принцип суперпозиции для магнитного поля?
5. Сформулируйте закон Био-Савара-Лапласа. Нарисуйте соответствующую картинку. Укажите направление векторов
6. Какова размерность вектора магнитной индукции в СИ? Напряжённости? Как они связаны между собой?
7. Используя закон Био-Савара-Лапласа, рассчитайте индукцию магнитного поля кругового тока.
8. В чем состоит метод определения горизонтальной составляющей индукции магнитного поля Земли? Получите расчётную формулу (3.3.11).
Лабораторная работа 3.4 Изучение магнитных свойств ферромагнетиков Цель работы: изучение гистерезиса ферромагнитных материалов, расчёт и графическое построение основной кривой намагничивания, определение магнитной проницаемости, расчёт работы перемагничивания и коэрцитивной силы. Теоретическое введение Электрические токи создают в окружающем пространстве магнитное поле. Поле, в свою очередь, действует на другие проводники с токами (сила Ампера). Можно сказать, что токи взаимодействуют посредством магнитного поля: поле – материальный посредник в таком взаимодействии. Силовая векторная характеристика магнитного поля – это магнитная индукция Магнитное поле создают также любые намагниченные тела, например постоянный магнит. Магнитная стрелка компаса, взаимодействуя с магнитным полем Земли, устанавливается в этом поле параллельно линиям магнитной индукции (рис. 3.4.1), указывая своим северным концом (N) на южный магнитный полюс Земли (S), приблизительно совпадающий с географическим Северным полюсом. Намагниченные тела, а также замкнутые витки с током (рис. 3.4.2), обладают магнитным моментом

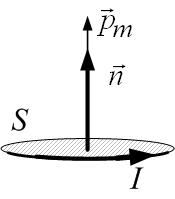 Здесь Здесь  – единичный вектор нормали к контуру ( – единичный вектор нормали к контуру (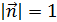 ), ), 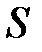 – площадь витка, I – сила тока. Магнитный момент – площадь витка, I – сила тока. Магнитный момент 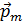 – вектор, направленный перпендикулярно плоскости витка по правилу буравчика (правого винта), если вращать буравчик по направлению тока. – вектор, направленный перпендикулярно плоскости витка по правилу буравчика (правого винта), если вращать буравчик по направлению тока.
Механический вращающий момент силы, действующий на магнитную стрелку или виток с током, пропорционален величине
где
Соотношение (3.4.3) позволяет ввести определение магнитной индукции
Однако магнитные свойства наиболее значимых для нашей жизни материалов – ферромагнетиков – определяются не орбитальным моментом электрона, а его спиновым (собственным) моментом Полный магнитный момент атома складывается из орбитальных В ненамагниченном состоянии магнитные моменты атомов вещества ориентированы хаотично, и суммарный магнитный момент макроскопического объёма магнетика равен нулю. Намагничивание вещества во внешнем магнитном поле – это появление ненулевого суммарного магнитного момента у вещества. Суммарный магнитный момент единицы объема магнетика называется намагниченностью:
Здесь
Обозначим
Напряженность магнитного поля Намагниченный магнетик создаёт своё собственное магнитное поле
Полная индукция поля в магнетике по принципу суперпозиции
или с учётом (3.4.6) и (3.4.7)
Для большинства магнетиков намагниченность пропорциональна напряжённости внешнего поля:
где
Обозначим
Тогда
Здесь
Магнитная проницаемость, как и восприимчивость, безразмерна: Формула связи индукции и напряжённости (3.4.12) работает не всегда, в общем случае эти векторы не параллельны; так что лучше использовать (3.4.9), откуда получим:
 В зависимости от знака и величины магнитной восприимчивости все вещества делятся на три группы: В зависимости от знака и величины магнитной восприимчивости все вещества делятся на три группы:· диамагнетики; · парамагнетики; · ферромагнетики. 1. Диамагнетики Диамагнетики во внешнем поле намагничиваются противоположно полю:
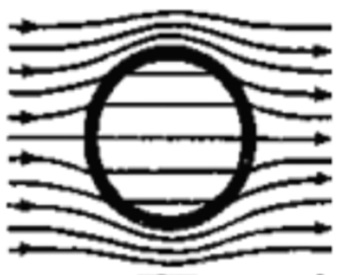
Для них магнитная восприимчивость Диамагнетики выталкиваются из магнитного поля. Газы, входящие в состав продуктов сгорания, диамагнитны, поэтому пламя свечи отклоняется в неоднородном магнитном поле в сторону слабого поля (рис. 3.4.5).
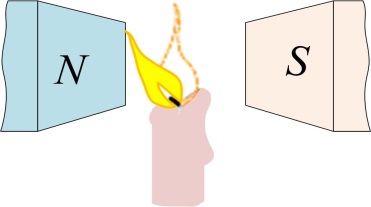 Диамагнитный эффект имеет место для всех веществ: и для пара-, и для ферромагнетиков. Но в пара- и ферромагнетиках диамагнитный эффект маскируется другими более сильными эффектами. Диамагнитный эффект имеет место для всех веществ: и для пара-, и для ферромагнетиков. Но в пара- и ферромагнетиках диамагнитный эффект маскируется другими более сильными эффектами.
2. Парамагнетики Парамагнетики – тоже слабомагнитные, но знак магнитной восприимчивости
 Индукция магнитного поля в парамагнетике больше, чем в вакууме. Магнитная проницаемость для них, как и для диамагнетиков, тоже мало отличается от единицы вследствие малости магнитной восприимчивости: Индукция магнитного поля в парамагнетике больше, чем в вакууме. Магнитная проницаемость для них, как и для диамагнетиков, тоже мало отличается от единицы вследствие малости магнитной восприимчивости: 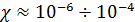 ; ; 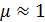 . .
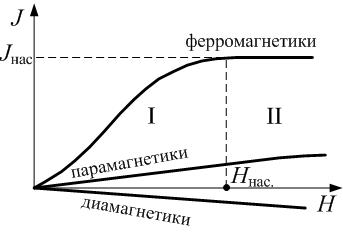
К парамагнетикам относятся вещества, магнитные моменты атомов (молекул, ионов) которых отличны от нуля: Полной ориентации магнитных моментов мешает тепловое движение, поэтому с повышением температуры магнитная восприимчивость уменьшается, намагниченность тоже уменьшается: 3. Ферромагнетики Ферромагнетики, в отличие от слабомагнитных диа- и парамагнетиков, являются сильномагнитными средами: внутреннее магнитное поле в них может в сотни и тысячи раз превосходить внешнее поле:
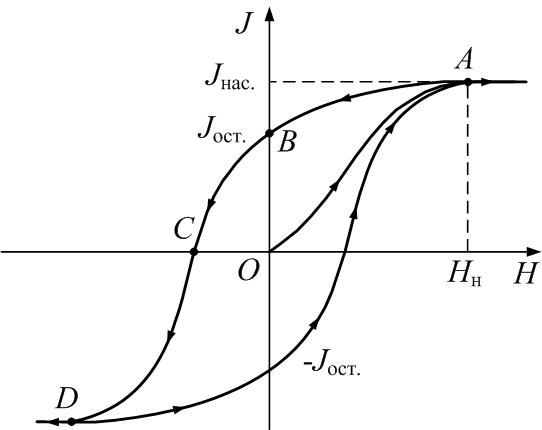
Такими свойствами обладают кристаллы переходных металлов (железо, кобальт, никель), некоторые редкоземельные элементы, ряд сплавов, а также некоторые металлические стёкла. Ферромагнетики в отсутствие внешнего поля могут обладать спонтанной (самопроизвольной) намагниченностью, зависящей от внешних воздействий – магнитного поля, деформации, температуры. Ферромагнетики намагничиваются параллельно внешнему полю: Перечислим свойства ферромагнетиков: 1. Зависимость намагниченности 2. Для ферромагнетиков характерно насыщение намагниченности: начиная с некоторого значения напряжённости H нас. внешнего поля, намагниченность, достигнув насыщения, перестаёт расти (рис. 3.4.7 и 3.4.8). 3. Магнитная восприимчивость зависит от предыстории. Если уменьшать напряжённость внешнего поля, то кривая АВ зависимости 4. Для ферромагнетиков характерен гистерезис. При дальнейших изменениях внешнего поля можно получить снова насыщение намагниченности, но уже противоположного знака (точка D, рис. 3.4.8), а затем замкнуть кривую намагниченности до точки А. Это – максимальный цикл. Если намагниченность не доводить до насыщения, периодически меняя направление и величину внешнего поля, можно получить частные циклы (рис. 3.4.9, кривые 2 и 3). Подобный график называется «петля гистерезиса». Само слово «гистерезис» значит «запаздывание»: изменения намагниченности J (или индукции В) запаздывают по сравнению с изменениями внешнего поля. 5.
 При нагревании выше некоторой температуры TC – температуры (точки) Кюри – ферромагнетик теряет свои свойства и превращается в парамагнетик. У каждого магнетика точка Кюри T C – своя; например, для железа это 1043 К. При нагревании выше некоторой температуры TC – температуры (точки) Кюри – ферромагнетик теряет свои свойства и превращается в парамагнетик. У каждого магнетика точка Кюри T C – своя; например, для железа это 1043 К.Природа ферромагнетизма
 В отличие от диа- и парамагнетизма, явление ферромагнетизма не может быть смоделировано в рамках классической физики; природа его – исключительно квантовая. В отличие от диа- и парамагнетизма, явление ферромагнетизма не может быть смоделировано в рамках классической физики; природа его – исключительно квантовая.
Ферромагнетизм обусловлен упорядоченной ориентацией спиновых магнитных моментов электронов. В атомах Fe, Ni и Co имеются не заполненные до конца внутренние электронные оболочки. Между такими атомами возникает особое взаимодействие – обменное. Оно связано с принципом неразличимости тождественных частиц: если два соседних атома обменяются электронами, то, в принципе, состояние не должно измениться (точнее, не меняется модуль волновой функции, которая в квантовой механике описывает состояние системы). Так что можно сказать, что обменные силы обусловлены волновыми свойствами электронов. В результате обменного взаимодействия возникают силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу (рис. 3.4.10, а). Это приводит к возникновению областей спонтанного намагничивания в кристалле ферромагнетика – доменов (рис. 3.4.11).
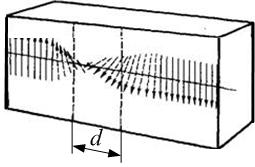
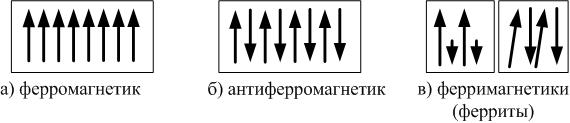
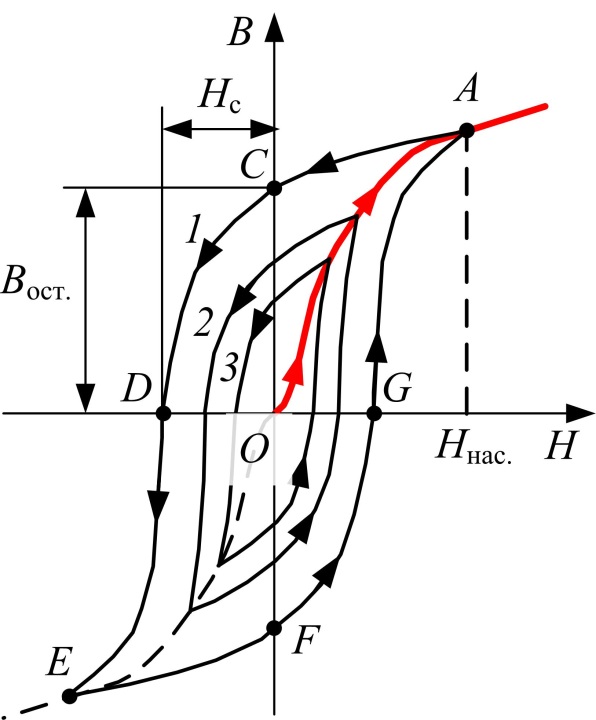
Спонтанное намагничивание сразу всего ферромагнетика оказывается энергетически невыгодным. Размеры домена порядка l ~10-8÷10-6 м. Между доменами есть тонкий переходный слой толщиной порядка d ~10-9÷10-8 м, в котором ориентация моментов меняется постепенно (рис. 3.4.12). Для антиферромагнетиков энергия обменного взаимодействия отрицательна, и спиновые магнитные моменты соседних атомов ориентируются противоположно друг другу (рис. 3.4.10, б); для них характерно отсутствие намагниченности. Рассмотрим процесс намагничивания ферромагнетика. Во внешнем поле происходит рост доменов, ориентированных по полю (рис. 3.4.13), а также скачкообразное изменение направления намагниченности доменов по полю – намагниченность растёт (область I на рис. 3.4.7), пока все домены не сориентируются по полю, и намагниченность образца достигнет насыщения (область II). Если ферромагнетик был первоначально размагничен (В =0, Н =0), то его намагничивание происходит по основной кривой намагничивания ОА (рис. 3.4.9). В точке А напряженность Н нас и индукция В нас соответствует состоянию магнитного насыщения. Размагничивание ферромагнетика происходит по кривой 1: A→ B ОСТ→(– H C)→A¢. Если внешнее поле убрать (Н =0), намагниченности доменов остаются ориентированными – это остаточная индукция: В = B ОСТ.
Размагнитить ферромагнетик можно, приложив поле противоположного направления. Напряжённость внешнего поля H С, при которой исчезает остаточная индукция B ОСТ, называется коэрцитивной силой, или коэрцитивным полем (см. рис. 3.4.9). Если при циклическом намагничивании H max≥ H c, то получается максимальная петля гистерезиса 1. Кривые 2 и 3 – это частные циклы, когда H max< H c. Максимумы В и Н частных циклов лежат на основной кривой намагничивания ОА.
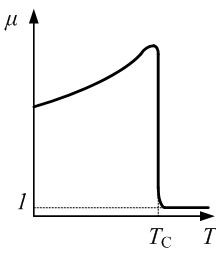
Зависимость магнитной проницаемости
Максимальное значение
 Строго говоря, для ферромагнетиков формулу (3.4.13) использовать нельзя, а магнитную проницаемость лучше определять не по абсолютным значениям Строго говоря, для ферромагнетиков формулу (3.4.13) использовать нельзя, а магнитную проницаемость лучше определять не по абсолютным значениям  и и  , а по их приращениям: , а по их приращениям:
При нагревании ферромагнетика его магнитная проницаемость увеличивается, так как облегчаются процессы смещения доменных границ. При температуре, равной или выше точки Кюри ТС в результате теплового движения ионов, находящихся в узлах кристаллической решетки, домены разрушаются, и материал переходит в парамагнитное состояние (рис. 3.4.15). 4. Ферримагнетизм Ферримагнетики (ферриты) состоят как бы из двух встроенных друг в друга решёток с магнитными моментами, направленными навстречу друг другу или имеющими более сложную пространственную ориентацию (рис. 3.4.10, в), но векторная сумма намагниченностей подрешёток отлична от нуля, поэтому для ферритов, как и для ферромагнетиков, характерна самопроизвольная намагниченность. Можно считать, что ферримагнетизм – наиболее общий случай магнитоупорядоченного состояния. Ферриты по своим электрическим свойствам – полупроводники: имеют удельное электрическое сопротивление, в миллиарды раз превышающее сопротивление металлических ферромагнетиков. Это практически исключает возникновение в ферритах вихревых токов в переменных магнитных полях. Благодаря таким уникальным свойствам ферриты находят широкое применение в радиоэлектронике. Магнитные материалы с прямоугольной петлёй гистерезиса широко применяются в устройствах автоматики, вычислительной техники, связи, хранения и переработке двоичной информации благодаря замечательной особенности: у таких материалов имеется два устойчивых магнитных состояния, соответствующих различным направлениям остаточной магнитной индукции. Двоичные элементы на магнитных сердечниках с прямоугольной петлёй гистерезиса характеризуются высокой надежностью, малыми габаритами, низкой стоимостью, относительной стабильностью характеристик. Они обладают практически неограниченным сроком службы, сохраняют записанную информацию при отключенных источниках питания. В табл. 3.4.1 приведены характеристики некоторых ферромагнетиков и ферритов. Таблица 3.4.1
Экспериментальная часть Приборы и оборудование: установка для исследования кривой намагничивания (источник постоянного напряжения, потенциометр, реостат, амперметр, переключатель, соленоид, ферромагнитный сердечник, тумблер, компас); вспомогательная установка для размагничивания (соленоид, понижающий трансформатор, потенциометр, реостат). Экспериментальная установка и методика измерений
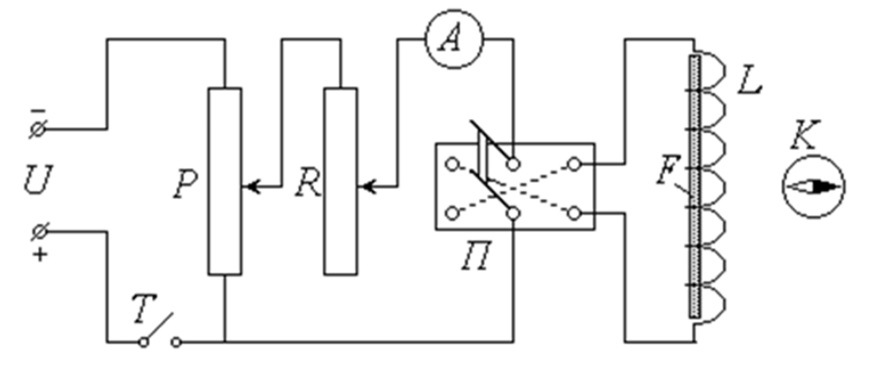 Питание лабораторной установки (рис. 3.4.16) осуществляется источником постоянного напряжения U; для замыкания цепи служит тумблер (выключатель) Т. Потенциометром Р можно регулировать подаваемое на установку напряжение, а реостатом R – силу тока в цепи. Для измерения тока в цепь включен амперметр А. С помощью переключателя П можно изменять направление тока через соленоид. Соленоид L представляет собой длинную прямую катушку, в которую помещается исследуемый образец (сердечник) – стержень F из ферромагнитного сплава. Питание лабораторной установки (рис. 3.4.16) осуществляется источником постоянного напряжения U; для замыкания цепи служит тумблер (выключатель) Т. Потенциометром Р можно регулировать подаваемое на установку напряжение, а реостатом R – силу тока в цепи. Для измерения тока в цепь включен амперметр А. С помощью переключателя П можно изменять направление тока через соленоид. Соленоид L представляет собой длинную прямую катушку, в которую помещается исследуемый образец (сердечник) – стержень F из ферромагнитного сплава.
Протекание тока I по виткам соленоида создает внутри него практически однородное магнитное поле, напряженность
где п – число витков, приходящееся на единицу длины соленоида. Для снятия петли гистерезиса необходимо измерять величину напряженности поля в соленоиде Н и соответствующую величину магнитной индукции в стержне В. Для определения магнитной индукции служит компас K. Перед началом опыта установка располагается таким образом, чтобы ось соленоида была перпендикулярна магнитному меридиану (рис. 3.4.17). В этом случае при отсутствии тока в соленоиде и отсутствии в нём сердечника (или при полном размагничивании последнего) стрелка компаса направлена в сторону горизонтальной составляющей индукции магнитного поля Земли
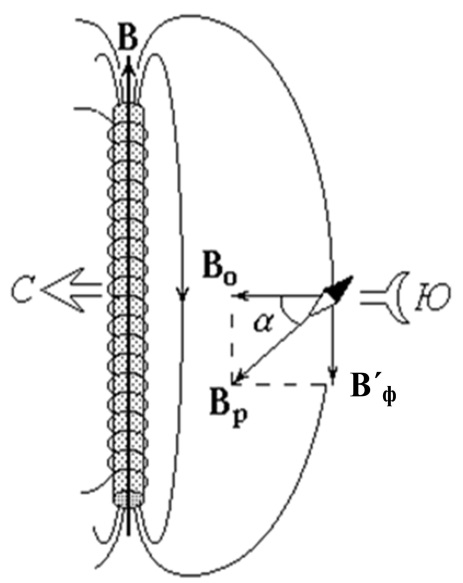 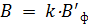 . (3.4.16) . (3.4.16)
Таким образом, стрелка компаса оказывается под воздействием двух магнитных полей: поля Земли с индукцией
С учетом (3.4.16) магнитная индукция в ферромагнитном сердечнике может быть рассчитана как
Для приведения ферромагнитного стержня в исходное размагниченное состояние используется вспомогательная установка, схема которой изображена на рис. 3.4.18. Стержень, подлежащий размагничиванию, также помещается в соленоид. Но, в отличие экспериментальной установки, эта установка питается
 через понижающий трансформатор Тр от сети переменного тока напряжением 220 В и частотой 50 Гц. После замыкания тумблера Т и увеличения (с помощью потенциометра Р и реостата R) силы тока в соленоиде стержень оказывается в переменном по величине и направлению магнитном поле; при этом с периодом 0,02 с «описываются», сменяя друг друга, все новые петли гистерезиса. Уменьшение тока от максимума до нуля приводит к тому, что петли «стягиваются» в точку 0, т.е. стержень полностью размагничивается. через понижающий трансформатор Тр от сети переменного тока напряжением 220 В и частотой 50 Гц. После замыкания тумблера Т и увеличения (с помощью потенциометра Р и реостата R) силы тока в соленоиде стержень оказывается в переменном по величине и направлению магнитном поле; при этом с периодом 0,02 с «описываются», сменяя друг друга, все новые петли гистерезиса. Уменьшение тока от максимума до нуля приводит к тому, что петли «стягиваются» в точку 0, т.е. стержень полностью размагничивается.
По площади петли гистерезиса можно найти работу перемагничивания, отнесенную к единице объёма. Малое изменение объёмной плотности энергии магнитного поля
Работа
Порядок выполнения работы 1. Ознакомьтесь с лабораторной установкой, запишите её номер. Запишите в табл. 3.4.2 значения числа витков на единицу длины соленоида п, коэффициента ослабления магнитного поля k и величину горизонтальной составляющей индукции магнитного поля Земли Таблица 3.4.2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.100 (0.018 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

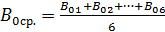 =
=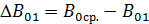 =
=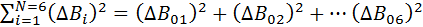 =
=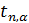 для
для  опытов и доверительной вероятности a = 0,95 равен
опытов и доверительной вероятности a = 0,95 равен 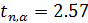 )
) =
=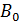 (для какого-либо одного конкретного опыта, например № 3 или 4; абсолютную приборную погрешность
(для какого-либо одного конкретного опыта, например № 3 или 4; абсолютную приборную погрешность 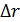 радиуса
радиуса  примите равной 5 мм)
примите равной 5 мм)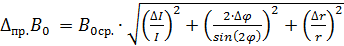 =
=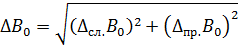 =
=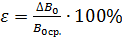 =
=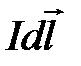 ,
, 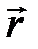 и
и 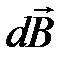 .
.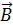 .
.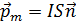 . (3.4.1)
. (3.4.1)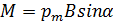 , (3.4.2)
, (3.4.2)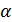 – угол между вектором магнитной индукции
– угол между вектором магнитной индукции 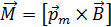 . (3.4.3)
. (3.4.3)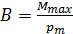 . (3.4.4)
. (3.4.4)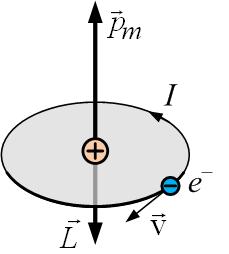
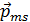 . Можно считать, что каждый электрон – это маленький магнитик. Однако нельзя представлять электрон как заряженный шарик, вращающийся вокруг своей оси и поэтому имеющий механический и магнитный моменты. Спин имеет не классическую природу, а квантовую, и не связан с движением электрона. Спином обладают многие частицы: у протона и нейтрона спин, как у электрона, равен
. Можно считать, что каждый электрон – это маленький магнитик. Однако нельзя представлять электрон как заряженный шарик, вращающийся вокруг своей оси и поэтому имеющий механический и магнитный моменты. Спин имеет не классическую природу, а квантовую, и не связан с движением электрона. Спином обладают многие частицы: у протона и нейтрона спин, как у электрона, равен  , а у фотона спин равен 1. Спин – неотъемлемое свойство электрона, как его масса или заряд.
, а у фотона спин равен 1. Спин – неотъемлемое свойство электрона, как его масса или заряд.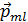 и спиновых
и спиновых 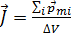 . (3.4.5)
. (3.4.5)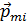 – магнитный момент i -того атома (молекулы); суммирование идёт по всем атомам в малом объёме
– магнитный момент i -того атома (молекулы); суммирование идёт по всем атомам в малом объёме 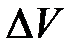 . Размерность намагниченности:
. Размерность намагниченности: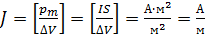 .
.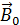 индукцию магнитного поля в вакууме, в отсутствие магнетика. Она создается только макротоками (токами проводимости). По определению, индукция магнитного поля в вакууме связана с напряженностью магнитного поля
индукцию магнитного поля в вакууме, в отсутствие магнетика. Она создается только макротоками (токами проводимости). По определению, индукция магнитного поля в вакууме связана с напряженностью магнитного поля 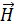 формулой:
формулой: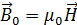 . (3.4.6)
. (3.4.6)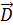 электростатического поля, который описывает только поле свободных зарядов и не зависит от наличия индуцированных зарядов в диэлектрике. Величина
электростатического поля, который описывает только поле свободных зарядов и не зависит от наличия индуцированных зарядов в диэлектрике. Величина 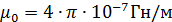 в (3.4.6) называется магнитной постоянной; это константа системы единиц СИ.
в (3.4.6) называется магнитной постоянной; это константа системы единиц СИ.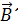 , накладывающееся на внешнее поле
, накладывающееся на внешнее поле 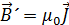 . (3.4.7)
. (3.4.7)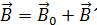 , (3.4.8)
, (3.4.8)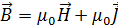 . (3.4.9)
. (3.4.9)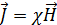 , (3.4.10)
, (3.4.10)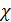 – магнитная восприимчивость вещества; она безразмерна:
– магнитная восприимчивость вещества; она безразмерна: 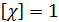 . Магнитная восприимчивость
. Магнитная восприимчивость 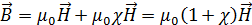
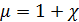 , (3.4.11)
, (3.4.11)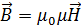 . (3.4.12)
. (3.4.12)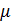 – магнитная проницаемость вещества. Её смысл можно сформулировать так: магнитная проницаемость показывает, во сколько раз индукция магнитного поля в веществе
– магнитная проницаемость вещества. Её смысл можно сформулировать так: магнитная проницаемость показывает, во сколько раз индукция магнитного поля в веществе 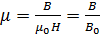 . (3.4.13)
. (3.4.13)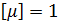 . Магнитная проницаемость вакуума, по определению, равна 1.
. Магнитная проницаемость вакуума, по определению, равна 1.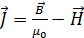 . (3.4.14)
. (3.4.14)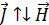 .
.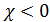 , магнитная проницаемость
, магнитная проницаемость 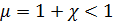 . Магнитная индукция в диамагнетиках меньше, чем в вакууме; густота линий индукции меньше (рис. 3.4.4). Диамагнетики – слабомагнитные вещества, так как значение
. Магнитная индукция в диамагнетиках меньше, чем в вакууме; густота линий индукции меньше (рис. 3.4.4). Диамагнетики – слабомагнитные вещества, так как значение 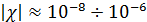 , а
, а 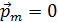 . Диамагнетиками являются инертные газы, молекулярные водород и азот, висмут, цинк, медь, золото,
. Диамагнетиками являются инертные газы, молекулярные водород и азот, висмут, цинк, медь, золото,  . Диамагнетизм объясняется либо откликом на внешнее магнитное поле электронных оболочек атомов, либо откликом обобществлённых электронов проводимости (металлы). Эффект диамагнетизма есть не что иное, как электромагнитная индукция на уровне электронных (по Амперу, «молекулярных») токов, присущих всем веществам.
. Диамагнетизм объясняется либо откликом на внешнее магнитное поле электронных оболочек атомов, либо откликом обобществлённых электронов проводимости (металлы). Эффект диамагнетизма есть не что иное, как электромагнитная индукция на уровне электронных (по Амперу, «молекулярных») токов, присущих всем веществам.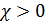 . Они намагничиваются параллельно внешнему полю:
. Они намагничиваются параллельно внешнему полю: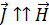 ,
, 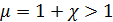 .
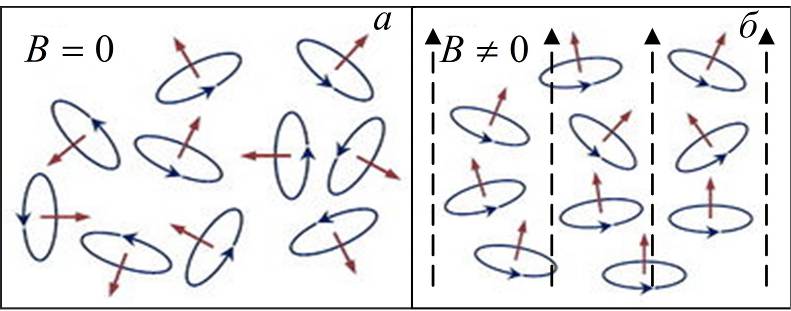
.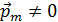 . Это – многие металлы (Al, Li, Na, K), некоторые газы (О2, NO). В отсутствие внешнего поля ориентация магнитных моментов атомов хаотична (рис. 3.4.6, а), и вещество в целом не имеет магнитного момента (не намагничено). Во внешнем магнитном поле магнитные моменты атомов ориентируются по полю (рис. 3.4.6, б), так как на них действует вращающий момент силы (3.4.2). Устанавливается некоторая преимущественная ориентация магнитных моментов атомов по полю, вещество приобретает магнитный момент, то есть намагничивается, причём намагниченность параллельна внешнему полю. Парамагнетики втягиваются в магнитное поле.
. Это – многие металлы (Al, Li, Na, K), некоторые газы (О2, NO). В отсутствие внешнего поля ориентация магнитных моментов атомов хаотична (рис. 3.4.6, а), и вещество в целом не имеет магнитного момента (не намагничено). Во внешнем магнитном поле магнитные моменты атомов ориентируются по полю (рис. 3.4.6, б), так как на них действует вращающий момент силы (3.4.2). Устанавливается некоторая преимущественная ориентация магнитных моментов атомов по полю, вещество приобретает магнитный момент, то есть намагничивается, причём намагниченность параллельна внешнему полю. Парамагнетики втягиваются в магнитное поле. .
.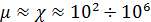 .
. от напряжённости поля
от напряжённости поля 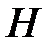 нелинейна:
нелинейна: 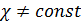 (рис. 3.4.7). На том же рисунке для сравнения приведены зависимости
(рис. 3.4.7). На том же рисунке для сравнения приведены зависимости 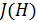 для пара- и диамагнетиков.
для пара- и диамагнетиков.
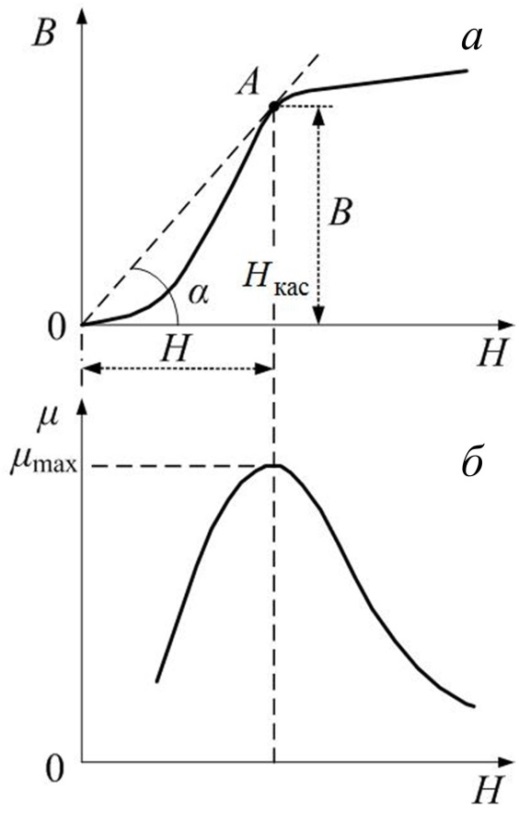
 от напряжённости поля можно получить графически. Из (3.4.13) следует, что для любой точки графика зависимости
от напряжённости поля можно получить графически. Из (3.4.13) следует, что для любой точки графика зависимости  магнитная проницаемость
магнитная проницаемость 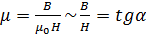 .
.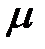 соответствует точке А касания на графике
соответствует точке А касания на графике 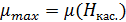 .
.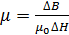 .
.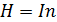 (3.4.15)
(3.4.15)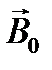 . При наличии магнитного поля в стержне его индукция
. При наличии магнитного поля в стержне его индукция 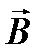 направлена вдоль оси соленоида (и стержня). Силовые линии магнитного поля замкнуты (две из них показаны на рисунке 3.4.17). Если компас расположен против середины соленоида (стержня), то индукция
направлена вдоль оси соленоида (и стержня). Силовые линии магнитного поля замкнуты (две из них показаны на рисунке 3.4.17). Если компас расположен против середины соленоида (стержня), то индукция 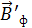 поля, создаваемого ферромагнетиком в центре компаса, направлена параллельно
поля, создаваемого ферромагнетиком в центре компаса, направлена параллельно 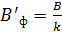 , откуда
, откуда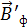 . В этом случае стрелка будет ориентирована в направлении результирующего поля с индукцией
. В этом случае стрелка будет ориентирована в направлении результирующего поля с индукцией 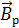 , отклонившись от магнитного меридиана на угол
, отклонившись от магнитного меридиана на угол 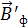 их модули связаны соотношением
их модули связаны соотношением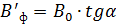 .
.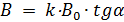 . (3.4.17)
. (3.4.17)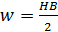 в цикле перемагничивания определяется по формуле
в цикле перемагничивания определяется по формуле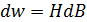 . (3.4.18)
. (3.4.18)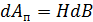 расходуется на изменение внутренней энергии единицы объёма ферромагнетика. За полный цикл перемагничивания работа равна площади петли гистерезиса, – это вытекает из смысла интеграла как площади под графиком функции:
расходуется на изменение внутренней энергии единицы объёма ферромагнетика. За полный цикл перемагничивания работа равна площади петли гистерезиса, – это вытекает из смысла интеграла как площади под графиком функции: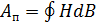 . (3.4.19)
. (3.4.19)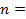 ………
………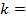 …………… м –1
…………… м –1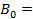 ……….. Тл
……….. Тл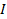 , А
, А
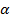 , град
, град
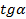
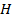 , А/м
, А/м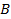 , Тл
, Тл