Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графиков на миллиметровой бумагеСодержание книги
Поиск на нашем сайте
1. На координатных осях указывают обозначения величин и их размерности. 2. Площадь чертежа используют максимально: график должен занимать примерно одинаковое пространство по обеим осям; при этом начало отсчёта можно сдвигать (если не указано, что график должен быть начерчен от 0). 3. Экспериментальные точки должны быть чёткими, яркими и одинаковой величины. 4. Масштабные деления на координатных осях наносят равномерно, а координаты экспериментальных точек не указывают и соответствующие точкам линии не проводят. 5. Масштаб должен быть удобен, чтобы положение любой точки можно было легко определить. Нельзя, например, использовать масштаб, в котором на 5 делений миллиметровки приходится 3 единицы измеряемой величины.
6. При значительном разбросе точек кривую или прямую проводят в среднем, то есть производят графическое усреднение (рис.1). Линию проводят так, чтобы она лежала как можно ближе к экспериментальным точкам, и чтобы по обе стороны от неё находилось примерно одинаковое число точек. Нельзя соединять первую и последнюю точки, как на рис. 2: тем самым игнорируются все остальные данные. На рис.1 представлен правильно построенный график зависимости l = f (m), на рис. 2 – график, оформленный с ошибками. Перечислим эти ошибки:
 1. Неверно выбраны координатные оси: масса m – независимая переменная, аргумент функции, должна откладываться по горизонтальной оси (оси абсцисс), а длина l пружины – функция массы – по оси ординат. 1. Неверно выбраны координатные оси: масса m – независимая переменная, аргумент функции, должна откладываться по горизонтальной оси (оси абсцисс), а длина l пружины – функция массы – по оси ординат.
2. Не указаны единицы измерения и не подписана ось абсцисс. 3. Площадь чертежа использована не полностью: была возможность сдвинуть начало координат для длины l. 4. Экспериментальные точки разной величины. 5. Масштабные деления для массы нанесены неравномерно (если есть 0.1, то должны быть 0.2, 0.3, 0.4, 0.5 и т.д.). 6. Вместо масштабных делений для длины нанесены координаты экспериментальных точек. 7. Проведены лишние пунктирные линии. 8. Выбран неудобный масштаб для длины. 9. Неправильно соединены экспериментальные точки: зависимость l = f (m) – линейная, и график представляет собой прямую линию. Полученные в результате экспериментов зависимости изображают в виде графиков не только для наглядности и удобства использования. Графическая обработка опытных данных – удобный и простой инструмент для определения измеряемых величин. Так, по графику зависимости длины
Коэффициент
На графике
Теперь из (16) и (17) можно найти 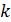 : :
Можно построить график в Excel, задав линейную линию тренда с требованием показывать уравнение
|
|||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 2351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.234 (0.01 с.) |

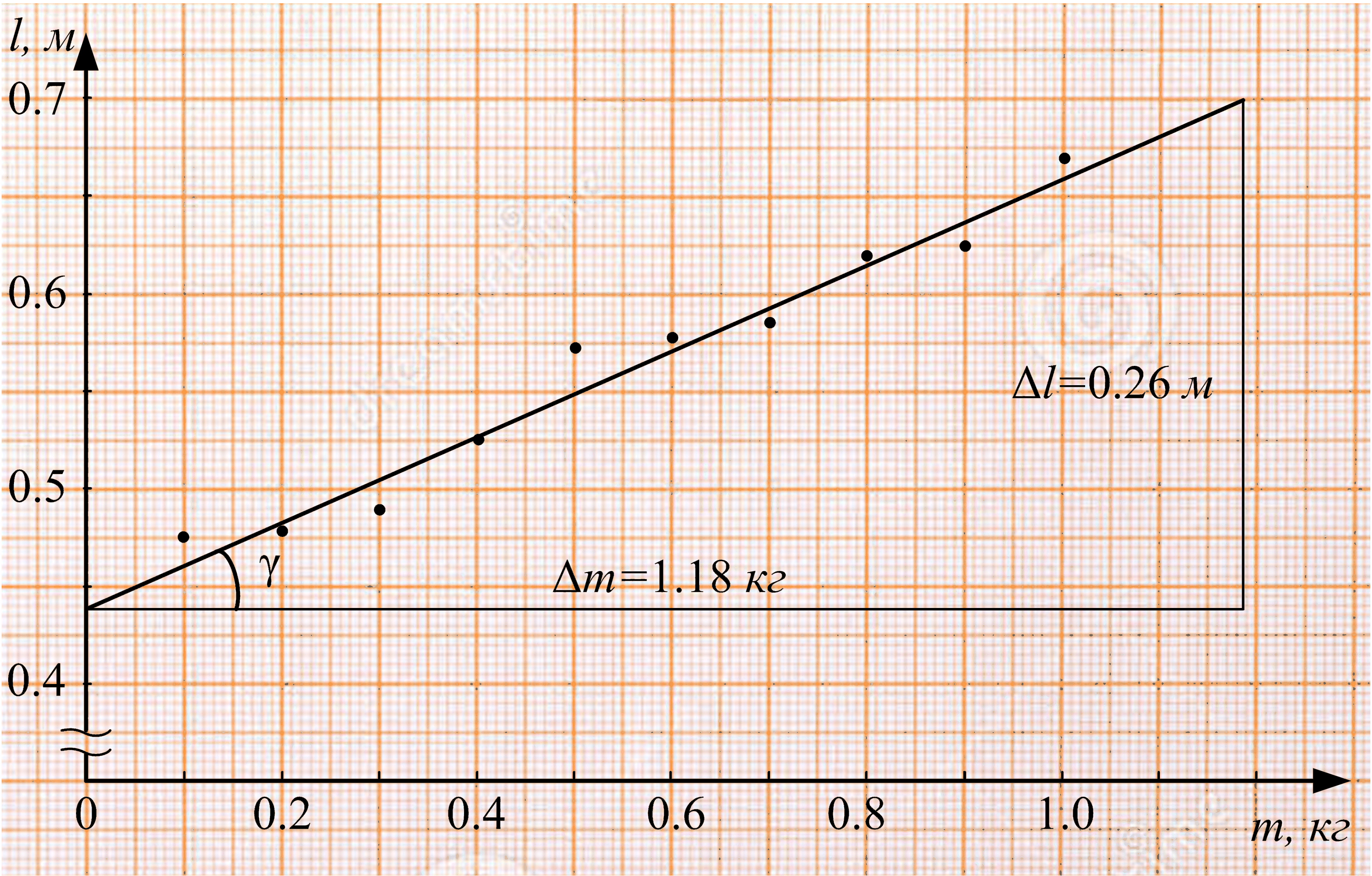
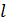 пружины от массы
пружины от массы 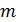 груза определяют жёсткость пружины
груза определяют жёсткость пружины 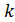 (рис. 1 и 3). По закону Гука зависимость
(рис. 1 и 3). По закону Гука зависимость 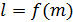 – линейная:
– линейная: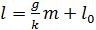 . (15)
. (15) при переменной
при переменной 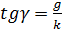 . (16)
. (16)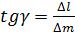 ; (17)
; (17)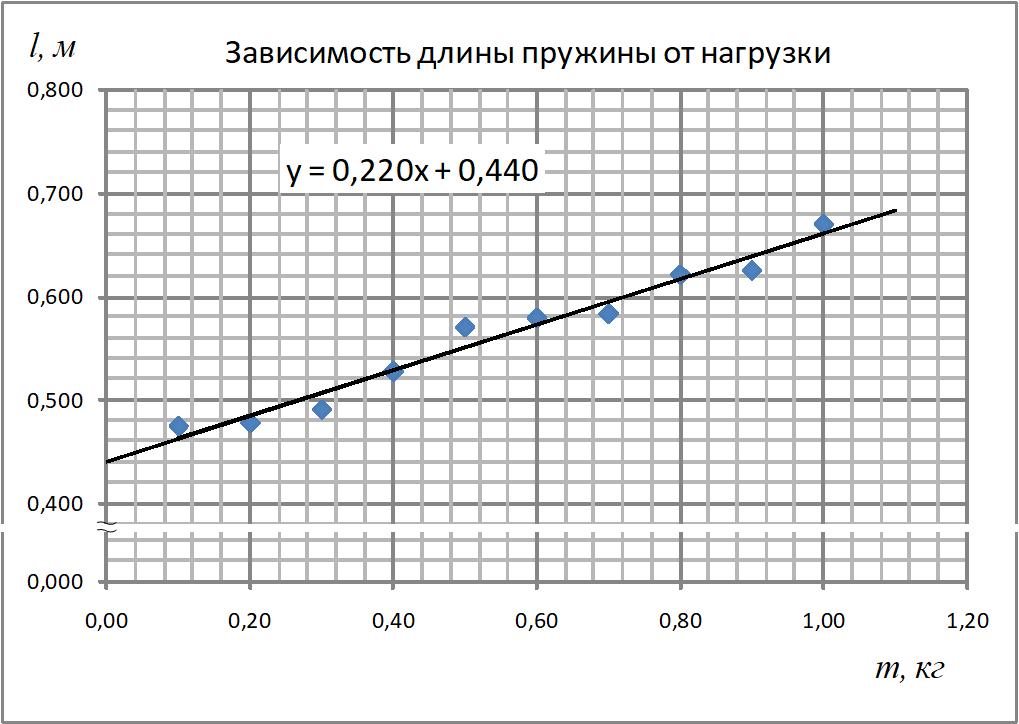
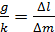 ;
;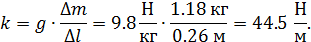
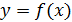 на диаграмме; тогда программа автоматически вычисляет угловой коэффициент – тангенс угла γ наклона графика к оси абсцисс. Из уравнения на рис. 3 коэффициент при независимой переменной
на диаграмме; тогда программа автоматически вычисляет угловой коэффициент – тангенс угла γ наклона графика к оси абсцисс. Из уравнения на рис. 3 коэффициент при независимой переменной 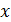 :
: 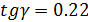 , откуда жёсткость
, откуда жёсткость