
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Место для построения графикаСодержание книги
Поиск на нашем сайте
Расчет момента инерции по графику
Момент сил трения по графику
Проверка выполнения закона сохранения энергии
Вывод о выполнении закона сохранения энергии:
Выводы по работе:
Контрольные вопросы и место для ответов 1. Дайте определения углового перемещения, угловой скорости, углового ускорения. Укажите направления этих векторов (сделайте рисунок). Запишите формулы, связывающие линейные и угловые величины перемещения, скорости, ускорения.
2. Дайте определение момента силы относительно точки; относительно оси. От чего он зависит? Как направлен вектор момента силы? Сделайте поясняющий рисунок.
3. Дайте определение момента инерции материальной точки; твёрдого тела. От чего он зависит?
4. Сформулируйте основной закон динамики вращательного движения.
5. Сформулируйте теорему Штейнера (запишите формулу и сделайте поясняющий рисунок) и покажите, где в работе её можно использовать. Как и почему изменяется время движения гири, если грузы на спицах передвинуть ближе к оси вращения?
6. Выведите формулы (1.3.26) и (1.3.33).
7. Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.
РАЗДЕЛ 2
Лабораторная работа 2.2 Определение отношения теплоёмкостей газа методом адиабатического расширения
Цель работы: изучение первого начала термодинамики в различных изопроцессах; определение адиабатической постоянной для воздуха. Теоретическое введение Одно из важных понятий термодинамики – внутренняя энергия U тела (или системы тел). Внутренняя энергия – это полная энергия тела, за исключением кинетической энергии движения тела как целого (движения центра масс и вращения тела как целого) и потенциальной энергии тела во внешних полях. В различных процессах важна не величина самой внутренней энергии, а её изменение в данном процессе. Внутренняя энергия системы – это функция состояния, то есть она однозначно определяется состоянием системы. Изменение внутренней энергии в каком-либо процессе не зависит от пути перехода, а только от начального и конечного состояния. Внутреннюю энергию системы можно изменить за счёт совершения над системой работы и сообщения системе теплоты. (Считаем, что система закрытая, то есть, она не обменивается веществом с окружающей средой.) По закону сохранения энергии
Это – первое начало термодинамики: количество теплоты
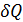 и работы и работы 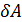 свойствами полного дифференциала не обладают, поскольку зависят от процесса, от пути перехода системы из одного состояния в другое. свойствами полного дифференциала не обладают, поскольку зависят от процесса, от пути перехода системы из одного состояния в другое.
Вычислим элементарную работу идеального газа, заключённого в цилиндре под поршнем, при изменении его объёма на
так как
Если при передаче телу теплоты
Физический смысл теплоёмкости тела:
Из (2.2.3) и (2.2.5) получим для молярной теплоёмкости (обозначаемой в дальнейшем как
При определении теплоёмкости необходимо указывать, каким именно способом изменяется температура: теплоёмкость, как и количество теплоты, зависит от вида процесса. При изохорном процессе работа не совершается (
Внутренняя энергия идеального газа равна
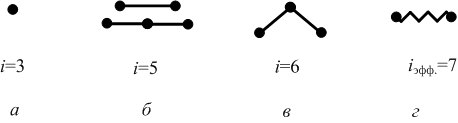
Она определяется температурой, количеством вещества и числом степеней свободы молекул i (числом независимых координат, однозначно определяющих положение молекулы в пространстве). Для одноатомных молекул i =3, так как трёх координат (x; y; z) достаточно для того, чтобы однозначно задать положение материальной точки в трёхмерном пространстве (рис.2.2.2, а). Для жёсткой многоатомной нелинейной молекулы расстояния между атомами и валентные углы фиксированы, тогда три координаты задают положение её центра масс (это три поступательных степени свободы: i пост.=3) и три угловых координаты (углы поворота относительно трёх взаимно перпендикулярных осей) задают ориентацию молекулы в пространстве: i вр.=3. Всего i = i пост+ i вр.=3+3=6 (рис. 2.2.2, в). В случае жёсткой двухатомной молекулы (или любой линейной молекулы, рис.2.2.2, б) одну вращательную степень свободы нужно исключить: вращение относительно оси молекулы не имеет смысла, так как атомы считаем материальными точками: i = i пост+ i вр.=3+2=5. При высоких температурах расстояния между атомами в молекуле изменяются, молекула не является жёсткой. Поэтому нужно учитывать степени свободы, связанные с изменением расстояний между атомами вследствие колебаний атомов (колебательные степени свободы). В случае двухатомной молекулы колебательная степень свободы одна: i кол.=1, – это расстояние между двумя атомами. Однако при колебаниях имеют место два вида энергии: кинетическая и потенциальная; поэтому колебательные степени свободы нужно удваивать. Вводят понятие эффективного числа степеней свободы:
i эфф.= i пост+ i вр.+2 i кол.. Для модели двухатомной молекулы «нежёсткая гантель» (две материальные точки на «пружинке», рис. 2.2.2, г) i эфф.= i пост+ i вр.+2 i кол=3+2+2.1=7.
 Колебательные степени свободы возбуждаются только при достаточно высоких температурах (тысячи кельвин), так что при обычных условиях их учитывать не надо. Из (2.2.7) и (2.2.8) получим изохорную теплоёмкость идеального газа:
Теплоёмкость
Найдём производную
Тогда из (2.2.10) получим уравнение Майера (2.2.12), и далее из (2.2.9) выразим
Соотношение (2.2.11) позволяет сформулировать физический смысл R: универсальная газовая постоянная – это работа одного моля идеального газа при изобарном нагреве на 1 кельвин. Во многих процессах важной характеристикой вещества является отношение теплоёмкостей
называемое также адиабатической постоянной, или показателем адиабаты, или показателем Пуассона. Из уравнения Майера можно получить:
По определению, адиабатный процесс происходит без теплообмена с окружающей средой:
Интегрируя последнее соотношение, получим уравнение адиабатического процесса:
Поскольку
Это – уравнение Пуассона. Величина Экспериментальная часть
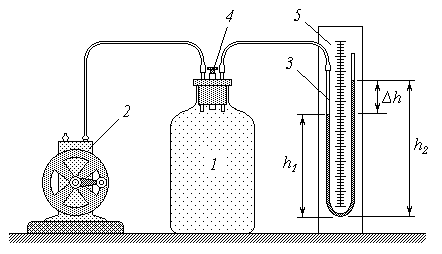 Приборы и оборудование: установка для определения адиабатической постоянной (сосуд, манометр, насос, линейка). Приборы и оборудование: установка для определения адиабатической постоянной (сосуд, манометр, насос, линейка).
|
||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.185.143 (0.011 с.) |

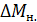 =
=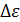 =
=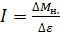 =
=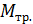 =
=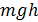 =
=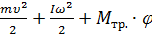 =
=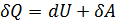 . (2.2.1)
. (2.2.1)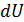 и на совершение работы
и на совершение работы 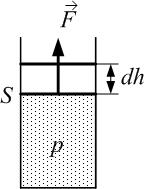
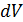 . При подъёме поршня (рис. 2.2.1) на малую высоту dh сила давления газа
. При подъёме поршня (рис. 2.2.1) на малую высоту dh сила давления газа 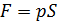 совершит работу
совершит работу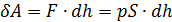 ,
,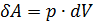 , (2.2.2)
, (2.2.2)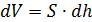 – изменение объёма газа. Тогда первое начало термодинамики можно записать так:
– изменение объёма газа. Тогда первое начало термодинамики можно записать так: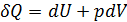 . (2.2.3)
. (2.2.3)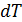 , то теплоёмкость тела:
, то теплоёмкость тела: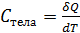 ;
; 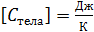 . (2.2.4)
. (2.2.4)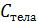 – это количество теплоты, необходимое для нагревания тела на 1 кельвин. Для характеристики вещества вводится понятие молярной теплоёмкости. Молярная теплоёмкость – это количество теплоты, которое необходимо для нагревания одного моля вещества на один кельвин:
– это количество теплоты, необходимое для нагревания тела на 1 кельвин. Для характеристики вещества вводится понятие молярной теплоёмкости. Молярная теплоёмкость – это количество теплоты, которое необходимо для нагревания одного моля вещества на один кельвин: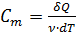 ;
; 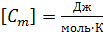 . (2.2.5)
. (2.2.5)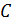 ):
):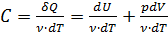 . (2.2.6)
. (2.2.6)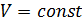 ;
; 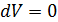 ), тогда молярная теплоёмкость
), тогда молярная теплоёмкость 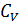 при постоянном объёме:
при постоянном объёме: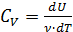 . (2.2.7)
. (2.2.7)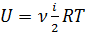 . (2.2.8)
. (2.2.8)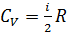 . (2.2.9)
. (2.2.9)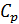 в изобарном процессе (
в изобарном процессе (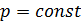 ) из (2.2.6)÷(2.2.9):
) из (2.2.6)÷(2.2.9):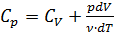 . (2.2.10)
. (2.2.10)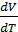 при
при 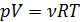 состояния идеального газа (уравнения Менделеева-Клапейрона):
состояния идеального газа (уравнения Менделеева-Клапейрона):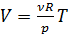
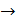
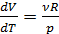
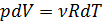 ;
;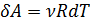 (2.2.11)
(2.2.11)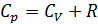 ; (2.2.12)
; (2.2.12)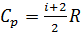 . (2.2.9а).
. (2.2.9а). , (2.2.13)
, (2.2.13)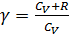
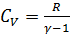 . (2.2.14)
. (2.2.14)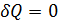 . Тогда по первому началу термодинамики:
. Тогда по первому началу термодинамики: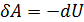
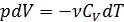
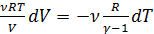 ,
,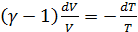 .
.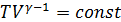 (2.2.15)
(2.2.15)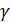 всегда больше единицы, то
всегда больше единицы, то 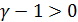 , и адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием газа. Используя уравнение Менделеева-Клапейрона, (2.2.15) можно преобразовать:
, и адиабатическое расширение сопровождается охлаждением, а сжатие – нагреванием газа. Используя уравнение Менделеева-Клапейрона, (2.2.15) можно преобразовать: (2.2.16)
(2.2.16)


