
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические характеристики вращательного движения
 Моментом силы Моментом силы  относительно точки О называется физическая величина, равная векторному произведению радиус-вектора относительно точки О называется физическая величина, равная векторному произведению радиус-вектора 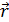 , проведенного из точки О в точку приложения силы, на вектор силы , проведенного из точки О в точку приложения силы, на вектор силы  : :
Направление момента силы определяется правилом буравчика (рис. 1.3.1), величина момента силы
где
Поворот тела с закреплённой осью вращения может быть вызван только касательной составляющей силы
так как
Учитывая (1.3.6) для касательного ускорения, получим из (1.3.10) и (1.3.11):
Скалярная величина
равная произведению массы материальной точки на квадрат её расстояния до оси, называется моментом инерции материальной точки относительно оси. Векторы
Уравнение (1.3.14) является основным законом динамики вращательного движения для материальной точки. Соотношение, аналогичное (1.3.12), можно записать для каждой точки тела, и затем просуммировать по всем точкам, тогда (с учётом того, что угловое ускорение одинаково для всех точек и его можно вынести за знак суммы):
В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (1.3.15) остается суммарный момент только внешних сил. Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твёрдого тела относительно данной оси:
Моментинерции
Таким образом, угловое ускорение твёрдого тела прямо пропорционально суммарному моменту внешних сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения:
Это – основной закон динамики твёрдого тела. Он аналогичен второму закону Ньютона при поступательном движении
и позволяет определить угловое ускорение Подсчёт момента инерции тела относительно произвольной оси облегчается применением теоремы Штейнера (1.3.20): момент инерции тела
Экспериментальная часть Приборы и оборудование: лабораторная установка, секундомер, линейка. Основным элементом маятника Обербека (рис. 1.3.2) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая
Методика измерений Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением
В проекциях на направление движения груза:
Массами нити 5 и блока 6 пренебрегаем; тогда натяжение нити по всей длине одинаково, и нить действует на поверхность шкива касательной силой, равной по модулю силе
С учетом (1.3.22) вращающий момент силы натяжения нити равен
Под действием момента
Здесь Так как нить 5 практически нерастяжима, все её точки, включая точки на поверхности шкива, движутся с одинаковым ускорением, равным по модулю ускорению падающего груза
Измерив высоту h и время падения груза t, можем найти ускорение
Далее, из (1.3.23) можно рассчитать момент силы натяжения нити, если известны масса груза т и радиус шкива R:
Угловое ускорение шкива и тангенциальное ускорение точек на поверхности шкива связаны соотношением (см. 1.3.6)):
Рассмотрим превращение энергии. Поднятый на высоту
Кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет неё груз приобретает кинетическую энергию
а крестовина – кинетическую энергию вращения
Здесь Изменение полной механической энергии равно работе сил трения
Работа при вращательном движении равна произведению момента
Знак «–» отражает тот факт, что работа сил трения и сопротивления всегда отрицательна. С учетом соотношений (1.3.28)÷(1.3.32) получим:
Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения (при
Используя связь между линейной и угловой скоростями, получим
Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол j (в радианах) может быть рассчитан как
Порядок выполнения работы 1. Запишите радиус R в таблицу 1.3.1, выразив его в метрах (R =17 мм). 2. Занесите во второй столбец таблицы 1.3.1 значение массы груза т (в кг). 3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты. 4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.3.1. Таблица 1.3.1
5. Повторите пункты 3 и 4 с тем же грузом ещё два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t. 6. Увеличивая массу груза согласно рекомендациям, выполните пункты 2-5 ещё пять раз. 7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (1.3.25), подставляя в неё среднее значение времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в таблицу 1.3.1. 8. По формулам (1.3.26) и (1.3.27) вычислите значения момента силы натяжения нити 9. Постройте график зависимости углового ускорения от момента силы натяжения 10. Найдите значения момента инерции крестовины 11. Для одного из проделанных опытов рассчитайте по формулам (1.3.34)÷(1.3.36) скорость груза 12. Вычислите значения левой и правой частей уравнения закона сохранения (изменения) энергии (1.3.33). Сравнив эти значения между собой, сделайте выводы. 13. Запишите общий вывод по работе. Расчеты: Пример расчёта среднего арифметического времени
Пример расчёта ускорения
Пример расчёта момента силы натяжения нити
Пример расчета углового ускорения
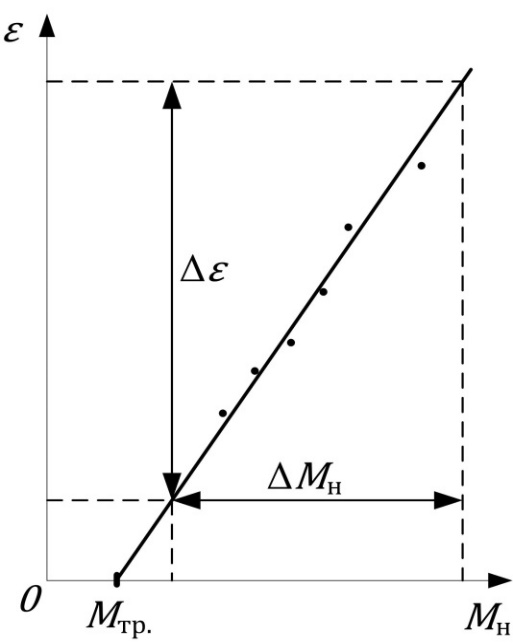
Обработка зависимости График зависимости 1) В Excel строим график, используя линейный тренд и требование показать уравнение зависимости
где
 Сравнение (1.3.37) и (1.3.38) даёт: 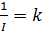 ; ; 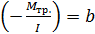 , или , или
2) Построение графика на миллиметровой бумаге. Нанесите на график экспериментально полученные точки. По точкам проведите сглаживающую прямую (рис. 1.3.3). Из уравнения (1.3.24) следует, что угловое ускорение
Примеры расчета: · линейной скорости υ
· угловой скорости вращения
· угла поворота
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.129.100 (0.078 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . (1.3.7)
. (1.3.7) , (1.3.8)
, (1.3.8)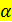 – угол между радиус-вектором
– угол между радиус-вектором 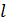 относительно оси ОО ’ как расстояние от оси вращения до линии действия силы, тогда
относительно оси ОО ’ как расстояние от оси вращения до линии действия силы, тогда ,
,  . (1.3.9)
. (1.3.9) , причём эта составляющая тем успешнее осуществит поворот, чем больше её плечо r:
, причём эта составляющая тем успешнее осуществит поворот, чем больше её плечо r: , (1.3.10)
, (1.3.10) . Пусть твёрдое тело разбито на отдельные элементарные массы Δ m. По второму закону Ньютона касательная составляющая равнодействующей сил, приложенных к этой точке, равна:
. Пусть твёрдое тело разбито на отдельные элементарные массы Δ m. По второму закону Ньютона касательная составляющая равнодействующей сил, приложенных к этой точке, равна: . (1.3.11)
. (1.3.11) . (1.3.12)
. (1.3.12) , (1.3.13)
, (1.3.13) и
и  совпадают по направлению с осью вращения, связаны с направлением вращения по правилу правого винта, поэтому равенство (1.3.12) можно переписать в векторной форме:
совпадают по направлению с осью вращения, связаны с направлением вращения по правилу правого винта, поэтому равенство (1.3.12) можно переписать в векторной форме: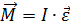 . (1.3.14)
. (1.3.14) . (1.3.15)
. (1.3.15) . (1.3.16)
. (1.3.16)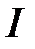 твёрдого тела является мерой инертных свойств твёрдого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он зависит не только от массы тела, но и от её распределения относительно оси (в направлении, перпендикулярном оси). В случае непрерывного распределения массы сумма в (1.3.16) сводится к интегралу по всему объёму (по массе) тела:
твёрдого тела является мерой инертных свойств твёрдого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он зависит не только от массы тела, но и от её распределения относительно оси (в направлении, перпендикулярном оси). В случае непрерывного распределения массы сумма в (1.3.16) сводится к интегралу по всему объёму (по массе) тела: . (1.3.17)
. (1.3.17) . (1.3.18)
. (1.3.18) (5.19)
(5.19)
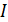 относительно любой оси равен сумме момента инерции
относительно любой оси равен сумме момента инерции 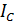 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния 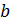 между осями.
между осями.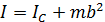 . (1.3.20)
. (1.3.20)
 , которое определяется вторым законом Ньютона (1.3.21). На груз действуют две силы: сила тяжести
, которое определяется вторым законом Ньютона (1.3.21). На груз действуют две силы: сила тяжести 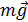 и сила натяжения нити
и сила натяжения нити  , тогда:
, тогда: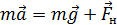 . (1.3.21)
. (1.3.21) ,
, . (1.3.22)
. (1.3.22) . Она создаёт вращающий момент
. Она создаёт вращающий момент  , по модулю равный произведению модуля силы на её плечо, равное радиусу шкива R:
, по модулю равный произведению модуля силы на её плечо, равное радиусу шкива R: . (1.3.22)
. (1.3.22)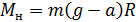 . (1.3.23)
. (1.3.23)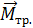 , направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения (1.3.18) имеет вид
, направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения (1.3.18) имеет вид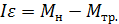 . (1.3.24)
. (1.3.24) , согласно уравнению (1.3.24), имеет линейный характер. Определив опытным путем значения
, согласно уравнению (1.3.24), имеет линейный характер. Определив опытным путем значения 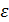 при различных
при различных 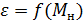 , с помощью этого уравнения можно найти неизвестные величины
, с помощью этого уравнения можно найти неизвестные величины 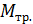 .
.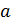 . Груз падает с высоты h равноускоренно; при этом за время t он проходит путь
. Груз падает с высоты h равноускоренно; при этом за время t он проходит путь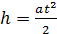 .
. . (1.3.25)
. (1.3.25)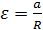 . (1.3.27)
. (1.3.27) груз обладает потенциальной энергией
груз обладает потенциальной энергией . (1.3.28)
. (1.3.28)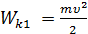 , (1.3.29)
, (1.3.29) . (1.3.30)
. (1.3.30) – скорость груза в момент падения;
– скорость груза в момент падения;  – угловая скорость вращения крестовины к этому моменту.
– угловая скорость вращения крестовины к этому моменту. :
: (1.3.31)
(1.3.31) :
: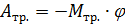 . (1.3.32)
. (1.3.32) . (1.3.33)
. (1.3.33)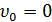 ):
): . (1.3.34)
. (1.3.34) . (1.3.35)
. (1.3.35) . (1.3.36)
. (1.3.36)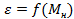
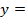 …………
………… =……….. c –2
=……….. c –2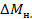 =……… Н × м
=……… Н × м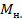 ,
Н × м
,
Н × м
 ,
Н × м
,
Н × м





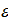 . Результаты занесите в табл. 1.3.1.
. Результаты занесите в табл. 1.3.1. и угол поворота
и угол поворота  =
= .
.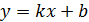 , (1.3.37)
, (1.3.37)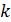 и
и 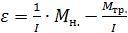 . (1.3.38)
. (1.3.38) ;
;  . (1.3.39)
. (1.3.39)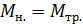 . Следовательно, момент сил трения
. Следовательно, момент сил трения 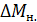 и
и 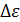 (с учетом масштаба графика) и рассчитайте значение
(с учетом масштаба графика) и рассчитайте значение 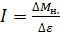 . (1.3.40)
. (1.3.40)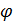 крестовины маятника Обербека в момент падения груза на пол
крестовины маятника Обербека в момент падения груза на пол


