
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение колебаний математического маятникаСодержание книги
Поиск на нашем сайте
Цель работы: изучение колебаний математического маятника и определение погрешности измерения ускорения свободного падения Теоретическое введение
При гармонических колебаниях колеблющаяся величина изменяется с течением времени по закону синуса или косинуса (4.1):
Здесь х – смещение колеблющейся точки от положения равновесия, А – амплитуда колебаний (абсолютное значение максимального смещения),
В (4.2) Скорость
Продифференцировав скорость (4.3), получим ускорение
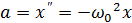 , или: , или:
Выражение (4.5) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Если вся масса маятника сосредоточена в одной точке (например, шарик, подвешенный на невесомой нерастяжимой нити), то такой маятник называют математическим (рис. 4.1). На шарик, подвешенный на нити, действуют сила тяжести
Сила натяжения нити
Отсюда
Вывод формул для расчёта погрешностей (для случая, когда все пять измерений производились в одних и тех же условиях: длина нити
1) Расчёт случайной погрешности
где n =5 – число опытов, 2) Расчёт случайной погрешности периода колебаний:
3) Вывод формулы для погрешности ускорения свободного падения при косвенных измерениях, исходя из (4.9):
Расчёт частных производных:
Подставляем частные производные в (4.11):
Абсолютную погрешность
Экспериментальная часть
Приборы и оборудование: секундомер, математический маятник (шарик на нити на штативе). 1. Длина математического маятника
Абсолютная погрешность длины определяется не приборной погрешностью линейки, а размерами груза маятника: примерно половина диаметра шарика, так как груз маятника точечным не является:
2. Число колебаний N =20. 3. Время t двадцати (N =20) колебаний измерено 5 раз (n =5) с одной и той же длиной l маятника; данные в таблице. Таблица. Результаты измерений и вычислений
4. Расчёт среднего арифметического времени двадцати колебаний:
5. Вычисление периода колебаний:
6. Вычисление ускорения свободного падения:
Расчёт погрешностей: 1. Вычисление отклонений от среднего времени:
2. Вычисление квадратов отклонений от среднего времени
3. Вычисление суммы квадратов отклонений от среднего времени:
4. Расчёт случайной погрешности времени:
5. Расчёт погрешности периода:
6. Расчёт относительной погрешности ускорения свободного падения по (4.13):
Абсолютная погрешность округления числа
7. Расчёт абсолютной погрешности ускорения свободного падения из (4.15):
8. Округление ускорения свободного падения в соответствии абсолютной погрешностью: ВЫВОД:
Экспериментальное значение в пределах погрешности
Вычисление погрешностей
Одна из задач лабораторного практикума – научиться правильно измерять физические величины. Измерение – это процесс сравнения физической величины с однородной величиной, принятой за единицу. Различают прямые и косвенные измерения. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно (например, определение длины стержня с помощью линейки) или при помощи измерительного прибора, проградуированного в соответствующих единицах (например, определение напряжения с помощью вольтметра). При косвенных измерениях измеряемая величина определяется (вычисляется) из результатов прямых измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Всякое измерение сопровождается погрешностью. Назовём абсолютной погрешностью
Более наглядное представление о точности измерений даёт относительная погрешность
Относительную погрешность выражают также в процентах:
Различают 2 класса погрешностей: случайные и систематические. Такие погрешности можно оценить, вычислить. Случайные погрешности – это такие погрешности, причины которых неизвестны и неконтролируемы; влияют на результат случайным образом, то в сторону его завышения, то в сторону занижения с равной вероятностью. Систематические погрешности – следствие несовершенства приборов (при прямых измерениях) или недостатков методов измерения (при косвенных измерениях). Систематические погрешности можно оценить, зная класс точности приборов, или анализируя метод измерения. Систематические погрешности влияют на результат односторонним образом, либо его систематически занижая, либо только завышая. Класс точности приборов указывается в виде числа на шкале прибора, например: 0.5; 1.0 (лабораторные приборы массового употребления). Класс точности даёт максимальную абсолютную погрешность, выраженную в процентах от предела измерения
Так, если предел измерения амперметра 50 мА (вся шкала рассчитана на 50 мА), а класс точности амперметра
Если при этом амперметр показывает ток 15 мА, то относительная погрешность составит
Если класс точности прибора не указан (простейшая линейка, например), то абсолютная приборная погрешность принимается равной половине цены деления:
Здесь цена деления – интервал измеряемой величины, соответствующий расстоянию между соседними штрихами на шкале прибора. Систематическая методическая погрешность при косвенных измерениях в той или иной мере есть всегда, поскольку на протекание любого явления влияет очень много факторов, и учесть их все невозможно. Систематическая погрешность вносится также при округлениях. При этом в соответствии с правилами округления абсолютная погрешность не превышает половины от единицы разряда последней оставленной при округлении значащей цифры. Принято записывать измеренную величину
Эта запись означает, что искомая величина с достаточно большой вероятностью, удовлетворяющей экспериментатора, попадёт в интервал от
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.90 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

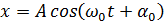 . (4.1)
. (4.1)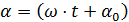 – фаза колебаний,
– фаза колебаний, 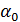 – начальная фаза,
– начальная фаза, 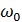 – собственная круговая (циклическая) частота, равная
– собственная круговая (циклическая) частота, равная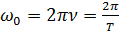 . (4.2)
. (4.2)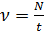 – частота колебаний (число полных колебаний в единицу времени,
– частота колебаний (число полных колебаний в единицу времени, 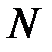 – число колебаний за время
– число колебаний за время 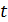 ),
), 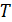 – период колебаний (время совершения одного полного колебания).
– период колебаний (время совершения одного полного колебания).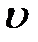 колеблющейся материальной точки получим, продифференцировав координату (4.1) по времени:
колеблющейся материальной точки получим, продифференцировав координату (4.1) по времени: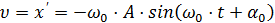 . (4.3)
. (4.3)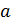 :
: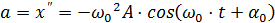 . (4.4)
. (4.4)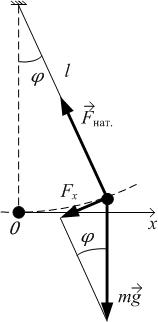
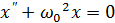 . (4.5)
. (4.5)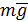 и сила натяжения нити
и сила натяжения нити 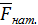 , тогда
, тогда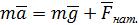 . (4.6)
. (4.6)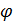 равна
равна 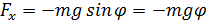 , тогда касательное ускорение
, тогда касательное ускорение 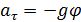 . Угол отклонения маятника из положения равновесия
. Угол отклонения маятника из положения равновесия 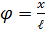 , где x – отклонение из положения равновесия. Касательное ускорение – это вторая производная координаты x, тогда
, где x – отклонение из положения равновесия. Касательное ускорение – это вторая производная координаты x, тогда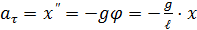 . (4.7)
. (4.7)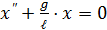 . Это дифференциальное уравнение гармонических колебаний идентично (4.5), если
. Это дифференциальное уравнение гармонических колебаний идентично (4.5), если 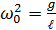 ; следовательно,
; следовательно,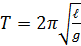 . (4.8)
. (4.8)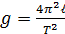 (4.9)
(4.9)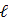 и число колебаний N одинаковы)
и число колебаний N одинаковы)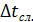 времени t N колебаний маятника по формуле Стьюдента:
времени t N колебаний маятника по формуле Стьюдента: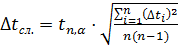 , (4.10)
, (4.10)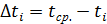 – отклонение от среднего в i -том опыте,
– отклонение от среднего в i -том опыте, 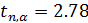 – коэффициент Стьюдента для доверительной вероятности α=0,95.
– коэффициент Стьюдента для доверительной вероятности α=0,95.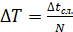 .
.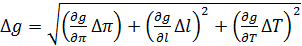 . (4.11)
. (4.11)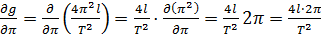 ;
;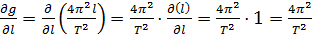 ;
;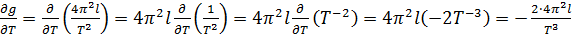 .
.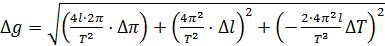 . (4.12)
. (4.12)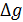 можно считать по (4.12), но расчёты упростятся, если сначала рассчитать относительную погрешность
можно считать по (4.12), но расчёты упростятся, если сначала рассчитать относительную погрешность 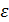 с учётом (4.9):
с учётом (4.9):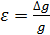 ;
; 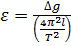
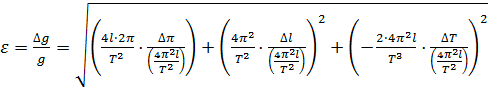 ;
;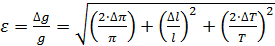 . (4.13)
. (4.13)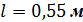 .
.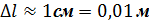 .
.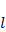 ,
м
,
м
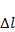 ,
м
,
м

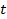 ,
с
,
с
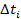 ,
с
,
с
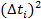 ,
c2
,
c2
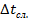 ,
с
,
с
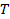 ,
с
,
с
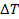 ,
с
,
с
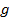 ,
м/с2
,
м/с2
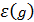 ,
%
,
%
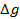 ,
м/с2
,
м/с2
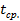 =30,72
=30,72
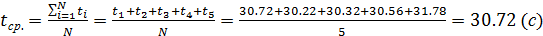 .
.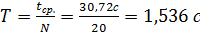 .
.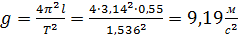 (4.14)
(4.14)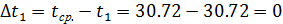 ;
;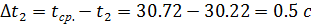 ;
;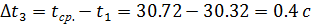 ;
; ;
;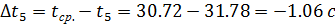 ;
;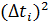 :
: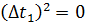 ;
;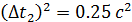 ;
;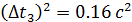 ;
;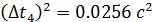 ;
;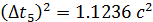 .
.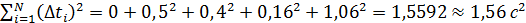 .
.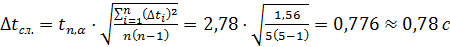 .
.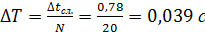 .
.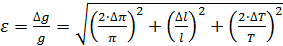 .
.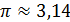 составляет
составляет 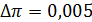 .
.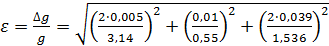 ;
;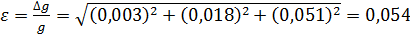 ;
;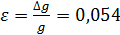 . (4.15)
. (4.15)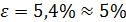 .
.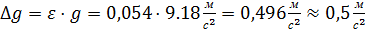 .
.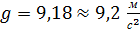 .
.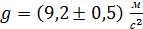 ;
;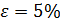 .
.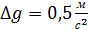 приблизительно равно табличному значению
приблизительно равно табличному значению 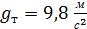 .
.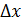 измерения какой-либо физической величины x модуль разности между истинным значением и измеренным:
измерения какой-либо физической величины x модуль разности между истинным значением и измеренным: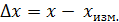 (1)
(1)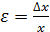 . (2)
. (2)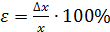 .
.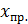 (максимального значения измеряемой величины):
(максимального значения измеряемой величины):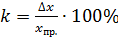 .
.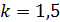 , то абсолютная приборная погрешность, даваемая амперметром, равна
, то абсолютная приборная погрешность, даваемая амперметром, равна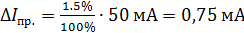 .
.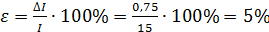 .
.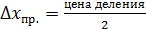 .
.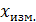 и её абсолютную погрешность
и её абсолютную погрешность 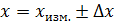 . (3)
. (3)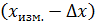 до
до  :
: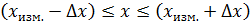 . (4)
. (4)


