
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт случайной погрешности по формуле СтьюдентаСодержание книги
Поиск на нашем сайте
Расчет относительной погрешности длины волны лазерного излучения в эксперименте
Выводы по работе:
Контрольные вопросы и место для ответа 1. Что такое интерференция волн?
2. Какие источники света называются когерентными? Почему естественные источники света не являются когерентными?
3. Дайте определения длины оптического пути; оптической разности хода лучей.
4. Получите условие интерференционного максимума; минимума. Запишите эти условия для разности фаз; для оптической разности хода.
5. Какой метод используется в оптике для получения когерентных световых волн? Опишите метод Юнга и выведите формулу (5.1.11) для ширины интерференционной полосы.
6. Опишите устройство бипризмы Френеля и объясните принцип её действия.
7. Как наблюдают кольца Ньютона? Опишите устройство установки, нарисуйте ход интерферирующих лучей.
8. Где применяется интерференция?
Лабораторная работа 5.3 Изучение законов теплового излучения Цель работы: ознакомление с законами теплового излучения, измерение постоянной Стефана-Больцмана. Теоретическое введение Поток световой энергии, падающий на поверхность непрозрачного тела, частично входит внутрь тела и поглощается. Поглощённая телом энергия преобразуется в другие формы энергии, чаще всего в энергию теплового движения. Поэтому тела, поглощающие лучи, нагреваются. Тело, нагретое до температуры, б о льшей, чем температура окружающей среды, отдаёт энергию в виде излучения электромагнитных волн. Всякое излучение сопровождается потерей энергии и происходит либо за счёт внутренней энергии, либо за счёт получения энергии извне. Излучение тела, обусловленное тепловым движением частиц, называется тепловым, так как происходит за счёт энергии теплового движения. Любое тело с температурой, б о льшей абсолютного нуля, излучает, причём спектр излучения – сплошной. Если уменьшение энергии тела при излучении восполняется за счёт поглощения излучения, падающего на тело, то излучение называется равновесным. Тепловое излучение тел может быть охарактеризовано двумя основными величинами: 1. Полная (интегральная) энергетическая светимость численно равна энергии всех длин волн, излучаемой в единицу времени с единичной площади поверхности тела (энергетическая мощность излучения с единицы площади):
Эту величину называют также интегральной интенсивностью излучения. Она зависит от абсолютной температуры тела. 2. Спектральная плотность энергетической светимости, или монохроматическая (дифференциальная) интенсивность излучения, численно равна энергии, излучаемой в единицу времени с единичной площади поверхности тела в единичном интервале длин волн (5.3.2) или частот (5.3.2а).
Спектральная плотность энергетической светимости является функцией длины волны и температуры (5.3.2) или частоты и температуры (5.3.2а). Из определения вытекает связь между интегральной и монохроматической светимостями:
Из всей падающей на тело энергии 3. Величина, показывающая, какую долю энергии падающего излучения в интервале длин волн
Тело называется абсолютно чёрным (АЧТ), если поглощает всё излучение, падающее на него: для абсолютно черного тела Законы теплового излучения Закон Кирхгофа. Исходя из второго начала термодинамики, Кирхгоф показал, что условие теплового равновесия заключается в следующем: отношение спектральной плотности энергетической светимости к поглощательной способности тела не зависит от природы тела; является универсальной (одинаковой для всех тел) функцией длины волны и температуры (универсальная функция Кирхгофа):
Следовательно, если тело хорошо поглощает лучи с какой-либо длиной волны, то лучи с такой же длиной волны будет хорошо и излучать. Величина
Для многих тел поглощательную способность можно считать не зависящей от длины волны:
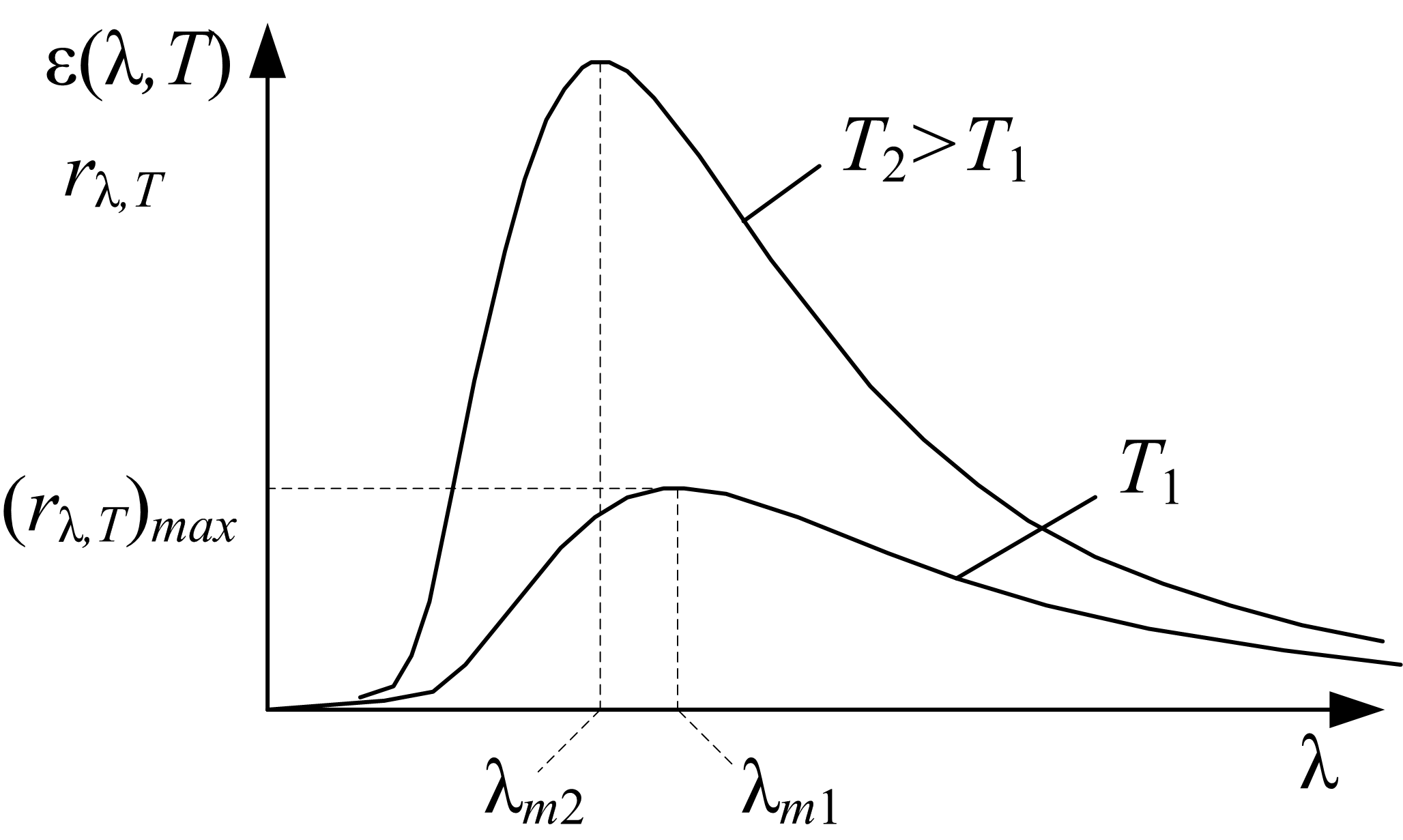 Эксперименты показали, что зависимость Эксперименты показали, что зависимость 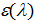 при различных температурах чёрного тела имеет вид, изображенный на рис. 5.3.2. По мере повышения температуры максимум смещается в область коротких волн, а интенсивность излучения растет. Эти закономерности излучения АЧТ описываются законами Вина. при различных температурах чёрного тела имеет вид, изображенный на рис. 5.3.2. По мере повышения температуры максимум смещается в область коротких волн, а интенсивность излучения растет. Эти закономерности излучения АЧТ описываются законами Вина.
Первый закон Вина (закон смещения Вина). Длина волны l m, на которую приходится максимум спектральной плотности энергетической светимости, обратно пропорциональна температуре:
Второй закон Вина. Максимальное значение спектральной плотности энергетической светимости прямо пропорционально пятой степени абсолютной температуры:
Первая и вторая константы Вина в (5.3.6.) и (5.3.7) равны соответственно:
В соответствии с (5.3.3) площадь под графиком функции
Постоянная Стефана-Больцмана s была определена опытным путём:
«Ультрафиолетовая катастрофа». Несмотря на детальное изучение характеристик теплового излучения, математический вид функции
Полученная ими формула
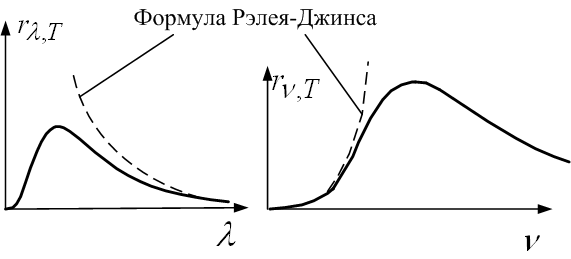 хорошо согласовывалась с данными опыта только в области малых частот излучения. На рис. 5.3.3 пунктир соответствует формуле Рэлея-Джинса; сплошная кривая – это экспериментальная зависимость. Для больших частот (5.3.11) даёт хорошо согласовывалась с данными опыта только в области малых частот излучения. На рис. 5.3.3 пунктир соответствует формуле Рэлея-Джинса; сплошная кривая – это экспериментальная зависимость. Для больших частот (5.3.11) даёт 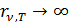 . Полная энергетическая светимость по формуле Рэлея-Джинса также равна бесконечности. С точки зрения классической физики вывод формулы Рэлея-Джинса безупречен, но она оказалась неверна. Классическая физика оказалась несостоятельной при описании теплового излучения. Невозможность решения проблемы теплового излучения методами классической физики назвали «ультрафиолетовой катастрофой». . Полная энергетическая светимость по формуле Рэлея-Джинса также равна бесконечности. С точки зрения классической физики вывод формулы Рэлея-Джинса безупречен, но она оказалась неверна. Классическая физика оказалась несостоятельной при описании теплового излучения. Невозможность решения проблемы теплового излучения методами классической физики назвали «ультрафиолетовой катастрофой».
Гипотеза и формула Планка. Причина «ультрафиолетовой катастрофы» оказалась лежащей чрезвычайно глубоко. Законы классической электродинамики давали неверный результат при рассмотрении элементарных процессов, обуславливающих тепловое излучение. Выход из создавшегося положения указал Макс Планк, выдвинув гипотезу, совершенно чуждую представлениям классической физики. Он предположил, что электромагнитное излучение испускается и поглощается дискретными порциями энергии – квантами электромагнитного поля (фотонами). Энергия такого кванта пропорциональна частоте колебания
а коэффициент пропорциональности h =6.63.10-34Дж.с – постоянная Планка – получил название в честь автора квантовой гипотезы. Так как излучение испускается порциями, то энергия квантового осциллятора ε может принимать лишь определённые дискретные значения, кратные целому числу элементарных порций энергии ε0:
Распределение квантовых осцилляторов по возможным дискретным состояниям подчиняется закону Больцмана; тогда средняя энергия квантового осциллятора, в отличие от классического (5.3.10), равна
где k= 1.38.10-23Дж/с – постоянная Больцмана. Исходя из того, что в состоянии термодинамического равновесия расход энергии на излучение осцилляторов с собственной частотой ν должен полностью компенсироваться в результате поглощения этими осцилляторами энергии падающего на них излучения, Планк показал, что
Тогда спектральная плотность энергетической светимости АЧТ равна
или, при переходе от частоты к длине волны:
Это и есть формула Планка. Если бы для определения средней энергии
Из формулы Планка можно получить также законы Вина, решив уравнение Тепловое излучение – единственное излучение, способное находиться в термодинамическом равновесии с веществом. При динамическом равновесии энергия, расходуемая телом на тепловое излучение, компенсируется вследствие поглощения этим телом такого же количества энергии падающего на него излучения. Отсюда следует, что если абсолютно чёрное тело находится в среде, имеющей температуру
Или, с учётом коэффициента серости,
Излучение накаливаемой током нити, покрытой окалиной, близко к излучению абсолютно черного тела. Приравнивая мощность
где I и U соответственно – сила тока и напряжение, а S – полная площадь поверхности нити. Используя (5.3.19), можно опытным путём определить постоянную Стефана - Больцмана:
Экспериментальная часть Приборы и оборудование: яркостный пирометр, исследуемая лампа, батарея питания, блок, содержащий амперметр и вольтметр, потенциометры, источники постоянного тока.
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.112.169 (0.008 с.) |

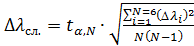 =
=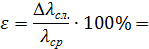
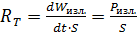 . (5.3.1)
. (5.3.1)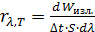 , (5.3.2)
, (5.3.2)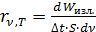 . (5.3.2а)
. (5.3.2а)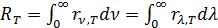 (5.3.3)
(5.3.3)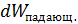 монохроматического света в интервале длин волн
монохроматического света в интервале длин волн 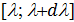 часть энергии
часть энергии 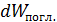 . поглощается телом.
. поглощается телом.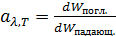 . (5.3.4)
. (5.3.4)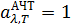 . В природе не существует абсолютно чёрных тел. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн. Наиболее совершенной моделью черного тела может служить небольшое отверстие в непрозрачной стенке замкнутой полости (рис.5.3.1). Луч света, попадающий внутрь через отверстие, претерпевает многократные отражения от стенок полости, прежде чем он выйдет обратно. При каждом отражении происходит частичное поглощение энергии света стенками. Поэтому независимо от материала стенок интенсивность света, выходящего из полости через отверстие, во много раз меньше интенсивности падающего извне первичного излучения. Эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия.
. В природе не существует абсолютно чёрных тел. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн. Наиболее совершенной моделью черного тела может служить небольшое отверстие в непрозрачной стенке замкнутой полости (рис.5.3.1). Луч света, попадающий внутрь через отверстие, претерпевает многократные отражения от стенок полости, прежде чем он выйдет обратно. При каждом отражении происходит частичное поглощение энергии света стенками. Поэтому независимо от материала стенок интенсивность света, выходящего из полости через отверстие, во много раз меньше интенсивности падающего извне первичного излучения. Эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия.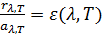 . (5.3.5)
. (5.3.5)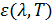 не зависит от природы тела и является функцией лишь длины волны и температуры. Так как для абсолютно черного тела
не зависит от природы тела и является функцией лишь длины волны и температуры. Так как для абсолютно черного тела 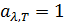 , то
, то 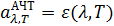 . Таким образом, универсальная функция Кирхгофа
. Таким образом, универсальная функция Кирхгофа 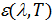 есть спектральная плотность энергетической светимости абсолютно черного тела. Для тел, не являющихся абсолютно чёрными,
есть спектральная плотность энергетической светимости абсолютно черного тела. Для тел, не являющихся абсолютно чёрными,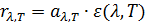 . (5.3.6)
. (5.3.6)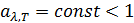 . Такие тела называются серыми, величина а называется коэффициентом серости (коэффициентом черноты).
. Такие тела называются серыми, величина а называется коэффициентом серости (коэффициентом черноты).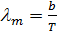 . (5.3.7)
. (5.3.7)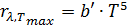 . (5.3.8)
. (5.3.8)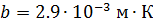 ,
,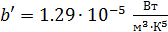 .
.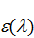 равна полной энергетической светимости АЧТ. По закону Стефана-Больцмана полная энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры:
равна полной энергетической светимости АЧТ. По закону Стефана-Больцмана полная энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры: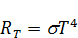 . (5.3.9)
. (5.3.9)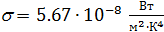 . Излучение серых тел подчиняется аналогичной закономерности, однако излучение их для каждой длины волны меньше, чем для абсолютно черного тела. Полное излучение
. Излучение серых тел подчиняется аналогичной закономерности, однако излучение их для каждой длины волны меньше, чем для абсолютно черного тела. Полное излучение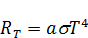 . (5.3.9а)
. (5.3.9а)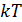 – одна половинка на электрическую, вторая – на магнитную энергию волны (по классическим представлениям на каждую степень свободы приходится в среднем энергия, равная
– одна половинка на электрическую, вторая – на магнитную энергию волны (по классическим представлениям на каждую степень свободы приходится в среднем энергия, равная 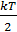 , то есть средняя энергия осциллятора
, то есть средняя энергия осциллятора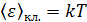 . (5.3.10)
. (5.3.10)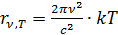 (5.3.11)
(5.3.11)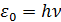 , (5.3.12)
, (5.3.12)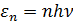 (n =0, 1, 2…).
(n =0, 1, 2…).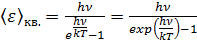 , (5.3.13)
, (5.3.13)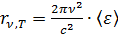 . (5.3.14)
. (5.3.14)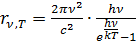 , (5.3.15)
, (5.3.15)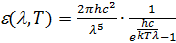 . (5.3.15а)
. (5.3.15а)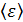 осциллятора Планк, подобно Рэлею, воспользовался законом классической статистики, он получил бы из (5.3.14) и (5.3.10) формулу Рэлея-Джинса (5.3.11). Формула Планка правильно описывает экспериментальную кривую рис. 5.3.2. На её основе были объяснены все экспериментально открытые законы теплового излучения, не находившие своего объяснения в рамках классической физики. Так, например, из (5.3.15) и (5.3.3) можно получить закон Стефана-Больцмана (5.3.9) интегрированием функции Планка по всему интервалу длин волн:
осциллятора Планк, подобно Рэлею, воспользовался законом классической статистики, он получил бы из (5.3.14) и (5.3.10) формулу Рэлея-Джинса (5.3.11). Формула Планка правильно описывает экспериментальную кривую рис. 5.3.2. На её основе были объяснены все экспериментально открытые законы теплового излучения, не находившие своего объяснения в рамках классической физики. Так, например, из (5.3.15) и (5.3.3) можно получить закон Стефана-Больцмана (5.3.9) интегрированием функции Планка по всему интервалу длин волн: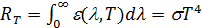 , (5.3.16)
, (5.3.16)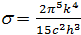 (5.3.17)
(5.3.17)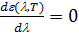 . Кроме того, формула Планка удовлетворяет принципу соответствия – в области малых частот, когда
. Кроме того, формула Планка удовлетворяет принципу соответствия – в области малых частот, когда 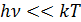 , формула (5.3.15) переходит в формулу Рэлея-Джинса (5.3.11).
, формула (5.3.15) переходит в формулу Рэлея-Джинса (5.3.11).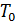 , и среду можно рассматривать как абсолютно чёрное тело, то поток поглощённой телом энергии определяется из закона Стефана-Больцмана:
, и среду можно рассматривать как абсолютно чёрное тело, то поток поглощённой телом энергии определяется из закона Стефана-Больцмана: 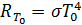 . Если температура тела
. Если температура тела 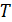 отличается от температуры среды
отличается от температуры среды 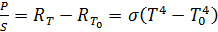 . (5.3.18)
. (5.3.18)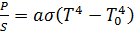 . (5.3.18а)
. (5.3.18а)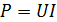 , затрачиваемую на поддержание нити в накаленном состоянии, и мощность, излучаемую с её поверхности, получаем выражение
, затрачиваемую на поддержание нити в накаленном состоянии, и мощность, излучаемую с её поверхности, получаем выражение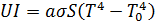 , (5.3.19)
, (5.3.19)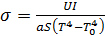 . (5.3.20)
. (5.3.20)


