
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт среднего арифметического значения показателя адиабатыСодержание книги
Поиск на нашем сайте
Пример расчёта отклонения от среднего значения показателя адиабаты
Расчёт суммы квадратов отклонений от среднего значения
Расчет абсолютной случайной погрешности
Расчет абсолютной приборной погрешности косвенного измерения показателя адиабаты (принять
Расчет полной абсолютной погрешности адиабатической постоянной с учётом случайной и приборной ошибок
Расчет полной относительной погрешности адиабатической постоянной с учётом случайной и приборной ошибок:
Выводы по работе:
Контрольные вопросы и место для ответов 1. Сформулируйте первое начало термодинамики (формула). Запишите его для изохорного, изотермического и адиабатического процессов (формулы).
2. Что такое внутренняя энергия? От чего она зависит? Запишите формулу для внутренней энергии идеального газа.
3. Что значит – «Внутренняя энергия – функция состояния системы?». Почему внутренняя энергия является функцией состояния, а теплота и работа – нет?
4. Как получить выражение для работы в термодинамике?
5. Запишите выражение для внутренней энергии идеального газа. Что такое число степеней свободы i? Эффективное число степеней свободы?
6. Дайте определения удельной и молярной теплоёмкостей (формулы). В каких единицах они измеряются и какова связь между ними?
7. Почему теплоёмкость газа зависит от способов и условий нагревания?
8. Почему
9. Какой процесс называется адиабатическим? Выведите уравнение Пуассона для адиабатического процесса.
10. Нарисуйте на p - V – диаграмме все процессы, происходящие с газом в этом опыте.
11. Покажите, что
12. Чему равна величина
РАЗДЕЛ 3
Лабораторная работа 3.1 Изучение закона Ома
Цель работы: знакомство с простейшими электрическими схемами и приобретение навыков работы с электроизмерительными приборами; экспериментальная проверка закона Ома для участка электрической цепи.
Теоретическое введение Электрический ток – направленное движение зарядов (заряженных частиц или заряженных тел; в последнем случае ток называется конвекционным). Сила тока – отношение заряда, прошедшего через сечение проводника, к промежутку времени, за которое заряд был перенесён:
Сила тока – производная заряда по времени. Только в случае, когда ток постоянный, можно использовать формулу
Плотность тока – это сила тока, приходящаяся на единицу площади сечения проводника:
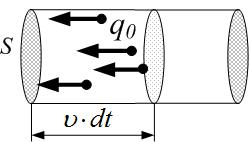 Здесь Здесь 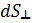 – малая площадка, перпендикулярная направлению переноса заряда. Плотность тока – вектор, направленный параллельно средней скорости – малая площадка, перпендикулярная направлению переноса заряда. Плотность тока – вектор, направленный параллельно средней скорости 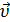 упорядоченного движения заряженных частиц (рис. 3.1.1). Размерность плотности тока: упорядоченного движения заряженных частиц (рис. 3.1.1). Размерность плотности тока:
Можно доказать, что
где n – концентрация частиц, q 0 – заряд каждой частицы. За время dt до сечения S дойдут частицы, находившиеся от сечения не дальше, чем на расстояние
Закон Ома для однородного участка цепи (то есть, участка, не содержащего ЭДС): сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению:
Получим формулировку закона Ома в дифференциальной (локальной) форме. Если поле в проводнике однородно, то напряжение на его концах равно
где Е – напряжённость поля. Сопротивление R участка выразим через удельное сопротивление проводника ρ
Тогда
Введём определение: удельная электропроводимость γ – это величина, обратная удельному сопротивлению:
Размерность удельной электропроводимости
Выражение (3.1.5) – это закон Ома в локальной (дифференциальной) форме: плотность тока прямо пропорциональна напряжённости поля. Заметим, что направления векторов плотности тока и напряжённости поля совпадают, независимо от того, какой знак у носителей тока. В выражении (3.1.5) вектор
Дело в том, что при наличии в проводнике только электростатических сил заряды в проводнике под их действием очень быстро перераспределятся, так что разность потенциалов любых точек проводника выравнивается; направленное движение зарядов в проводнике прекратится. Для того чтобы ток в проводнике поддерживался, электростатических сил недостаточно. Нужны силы неэлектростатического происхождения; их называют сторонними. Именно они действуют в источниках тока, разделяя положительные и отрицательные заряды. Сторонние силы направлены в источнике противоположно кулоновским (электростатическим). Природа этих сил может быть различна, например, в аккумуляторах это химические силы, в электрогенераторах – электромагнитные.
 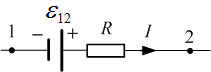
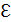 (ЭДС) и нагрузки (ЭДС) и нагрузки 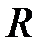 (резистора). По определению, ЭДС источника – это работа сторонних сил по переносу единичного заряда в замкнутой цепи (или на участке цепи, содержащем источник): (резистора). По определению, ЭДС источника – это работа сторонних сил по переносу единичного заряда в замкнутой цепи (или на участке цепи, содержащем источник):
ЭДС измеряется в вольтах:
Введём понятие напряжённости поля сторонних сил
Вычислим работу сторонних сил при переносе заряда q на участке цепи от точки 1 до точки 2 (рис. 3.1.3):
Тогда из (3.1.6):
Если контур замкнут (1=2), Именно сторонние силы совершают работу по переносу заряда в замкнутом контуре; работа кулоновских (электростатических) сил в замкнутом контуре равна нулю, так как электростатическое поле потенциально. Полная сила, действующая на заряд со стороны кулоновских и сторонних сил, равна:
а работа суммарной силы при переносе заряда на участке цепи
Здесь первый интеграл, взятый с противоположным знаком, равен разности потенциалов:
а второй интеграл – это ЭДС (3.1.8). Тогда
Напряжением на участке цепи называется суммарная работа кулоновских и сторонних сил по переносу единичного заряда на данном участке цепи:
Тогда с учетом (3.1.11) из (3.1.12) напряжение равно
Напряжение, как и ЭДС, и потенциал, измеряется в вольтах: Возможны частные случаи: а) Контур замкнут (1=2), тогда φ 1– φ 2=0, и напряжение в такой замкнутой цепи – это ЭДС: U = б) Напряжение на однородном участке цепи (то есть, не содержащем ЭДС:
Понятие напряжения является обобщением понятий как ЭДС, так и разности потенциалов. Закон Ома для неоднородного участка цепи (то есть для участка, содержащего источник тока) с ЭДС
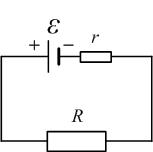
Закон Ома для полной цепи. Сила тока в замкнутой цепи (рис. 3.1.2) равна
где R – сопротивление нагрузки, r – внутреннее сопротивление источника тока, Для расчёта разветвлённых цепей постоянного тока, а также для не слишком быстро меняющихся (квазистационарных) токов используются правила Кирхгофа.
Первое правило Кирхгофа справедливо для любого узла разветвлённой цепи (узел – точка электрической цепи, в которой сходятся три или больше проводников): алгебраическая сумма токов, сходящихся в узле, равна нулю:
Токи, заходящие в узел, надо брать в этой сумме с положительным знаком, выходящие из узла – с отрицательным. Это правило – следствие закона сохранения заряда: если токи постоянные, то заряд в узле накапливаться не должен. Например, для узла на рис. 3.1.4 первое правило выглядит так:
Второе правило Кирхгофа. Алгебраическая сумма напряжений на всех участках любого замкнутого контура равна алгебраической сумме ЭДС, включенных в данный контур:
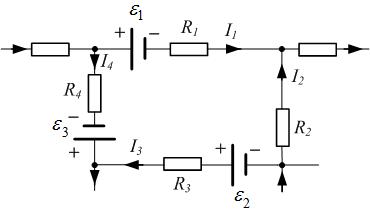 Правило знаков: если направление тока на данном участке совпадает с направлением обхода контура, то произведение (IR) i в сумме надо брать с положительным знаком; иначе – с минусом. Если ЭДС при обходе контура проходим от минуса к плюсу, то соответствующую ЭДС в сумме надо брать с плюсом; иначе – с минусом. Пример – см. рис. 3.1.5; обход контура по часовой стрелке:
Если в разветвлённой цепи N узлов, то по первому правилу нужно написать (N –1) уравнений; уравнение, составленное для последнего узла, будет линейной комбинацией предыдущих и не даст ничего нового. Общее число уравнений (по первому и по второму правилам Кирхгофа в сумме) равно числу ветвей (числу токов). Каждое новое уравнение по второму правилу должно включать новый фрагмент цепи (новую ветвь), ещё не описанную вторым правилом. Если уравнений столько, сколько нужно, они перекроют всю цепь, и не останется ни одной не описанной ветви цепи. Электронная теория проводимости металлов, разработанная Лоренцем и Друде, исходит из того, что: 1) Носители заряда в металле – электроны. 2) Электроны слабо связаны с кристаллической решёткой. 3) Электроны движутся как в идеальном газе, то есть можно рассматривать совокупность электронов в металле как идеальный электронный газ. 4) Электронный газ находится в термодинамическом равновесии с кристаллической решёткой. Теория позволила вывести законы Ома и Джоуля-Ленца, но другие её выводы с опытом не совпали. Например, теория даёт, что сопротивление металлов пропорционально корню из абсолютной температуры:
Экспериментальная часть Приборы и оборудование: установка для изучения закона Ома (блок питания, выпрямитель, потенциометр, вольтметр, миллиамперметр, ключ, магазин сопротивлений).
|
|||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.138 (0.008 с.) |

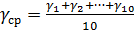 =
=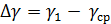 =
=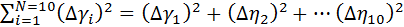 =
=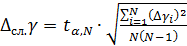 =
=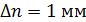 )
)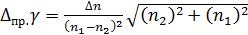 =
=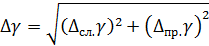 =
=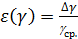 =
=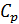 больше
больше 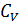 ? Получите уравнение Майера. В чём заключается физический смысл универсальной газовой постоянной?
? Получите уравнение Майера. В чём заключается физический смысл универсальной газовой постоянной?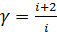 .
.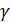 для одно-, двух-, трёхатомных газов согласно молекулярно-кинетической теории теплоёмкости идеальных газов?
для одно-, двух-, трёхатомных газов согласно молекулярно-кинетической теории теплоёмкости идеальных газов?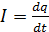 . (3.1.1)
. (3.1.1)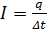 . Физический смысл величины I: сила тока численно равна заряду, проходящему через сечение проводника за единицу времени. Размерность:
. Физический смысл величины I: сила тока численно равна заряду, проходящему через сечение проводника за единицу времени. Размерность: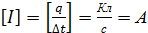 .
.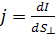 . (3.1.2)
. (3.1.2)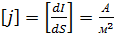 .
.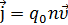 ,
,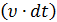 , то есть находящиеся в объёме
, то есть находящиеся в объёме 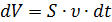 (рис. 3.1.1). Число таких частиц
(рис. 3.1.1). Число таких частиц 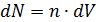 , а их суммарный заряд
, а их суммарный заряд 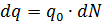 . Тогда плотность тока
. Тогда плотность тока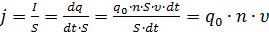 .
.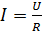 . (3.1.3)
. (3.1.3)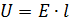 ,
,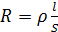 .
.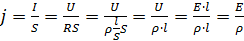 .
.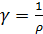 . (3.1.4)
. (3.1.4)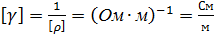 . С учётом (3.1.4) получим:
. С учётом (3.1.4) получим: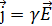 . (3.1.5)
. (3.1.5)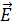 – это напряжённость суммарного поля кулоновских (электростатических) и сторонних (действущих в источниках тока) сил:
– это напряжённость суммарного поля кулоновских (электростатических) и сторонних (действущих в источниках тока) сил: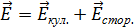 .
.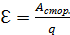 . (3.1.6)
. (3.1.6)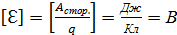 .
.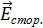 по аналогии с напряжённостью электростатического поля:
по аналогии с напряжённостью электростатического поля: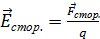 ,
, 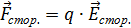 . (3.1.7)
. (3.1.7)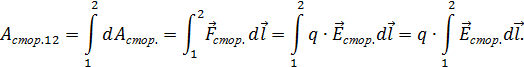
 (3.1.8)
(3.1.8)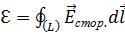 .
.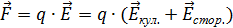 ,
,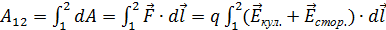 ;
;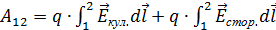 . (3.1.9)
. (3.1.9)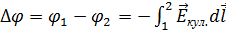 , (3.1.10)
, (3.1.10)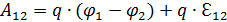 . (3.1.11)
. (3.1.11)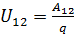 . (3.1.12)
. (3.1.12)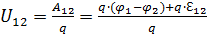 ,
,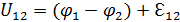 . (3.1.13)
. (3.1.13)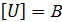 .
.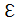 .
.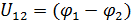 .
.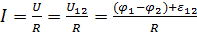 . (3.1.14)
. (3.1.14)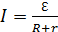 ,
,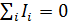 . (3.1.15)
. (3.1.15)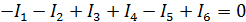 .
.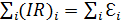 . (3.1.16)
. (3.1.16)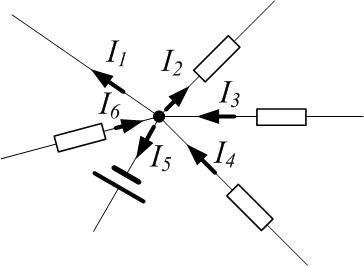
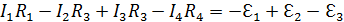 .
.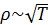 , что не совпадает с экспериментальными данными:
, что не совпадает с экспериментальными данными: 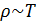 . Теплоёмкость металла теория тоже предсказала неверно. Эти трудности в рамках классической теории не могут быть преодолены, так как электронный газ – квантовый.
. Теплоёмкость металла теория тоже предсказала неверно. Эти трудности в рамках классической теории не могут быть преодолены, так как электронный газ – квантовый.


