
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения электропривода.Содержание книги
Поиск на нашем сайте
Поскольку преобразующий механизм станка–качалки (СК) является разновидностью кривошипно-шатунного механизма (рис. 2), его особенность заключается в нелинейной кинематической связи между ведомым валом редуктора и точкой подвеса штанг (далее – ТПШ). В этом случае приходится иметь дело с обобщенным уравнением движения электропривода [4]:
где ω – угловая скорость ротора приводного двигателя; JΣпр – суммарный приведенный момент инерции системы; McΣпр – суммарный приведенный момент сопротивления движению системы, М – вращающий момент, развиваемый двигателем.
Радиус приведения. Приведение параметров ТПШ к валу приводного двигателя представляет определенную сложность. Из-за громоздкости выражения, получаемого для ρТПШ(γкр), не представляется возможным использовать его в расчетах. Проблема была решена разложением ρТПШ(γкр) в ряд Фурье, что значительно ускорило обсчет модели. Для станков–качалок по ГОСТ5866-76 [1] рассчитаны наборы коэффициентов Фурье. Количество членов ряда – 14 первых членов разложения определялось из условия 5%–ной точности относительно непреобразованного выражения для ρТПШ(γкр).
На рис. 3 в качестве примера показана зависимость ρТПШ(γкр) станка-качалки СК–12–2,5–4000. Зависимость такова, что не может быть заменена одной синусоидой.
Нагрузка станка - качалки. При ходе плунжера вверх к ТПШ приложена статическая нагрузка, создаваемая весом столба жидкости Рж над плунжером, весом самих штанг с учетом действия архимедовой силы Р’ш и силами трения. Эта нагрузка не прикладывается внезапно, а постепенно возрастает в начальный период хода вверх, благодаря упругим деформациям штанг и труб, но в данной работе этот факт не учитываетя. Кроме статической нагрузки к ТПШ оказываются приложенными и динамические силы, возникающие вследствие инерционных свойств масс штанг, столба жидкости и продольных колебаний последних. При ходе плунжера вниз результирующая статическая нагрузка в ТПШ определяется весом штанг за вычетом веса, занимаемого ими объема жидкости Р’ш и сил трения. Вес жидкости над плунжером не действует на штанги. Так как верхний клапан насоса открыт, а нижний закрыт, то этот вес через нижний клапан передается насосным трубам. При изменении направления движения плунжера усилие в ТПШ не принимает мгновенно своего установившегося значения, а постепенно убывает вследствие упругих деформаций штанг и труб. Рж, Р’ш и Рш вычисляются по следующим формулам:
где dпл – диаметр плунжера; ρж – плотность жидкости; Lш – длина колонны штанг; dш –диаметр штанг; ρш – плотность материала штанг. Существует несколько функций, которые пригодны для описания пульсирующей нагрузки. Например,
где N – нечетное, порядка нескольких сотен. Тогда пульсирующая нагрузка в точке подвеса штанг описывается уравнением
Ниже (рис. 4) показан пример описания нагрузки в ТПШ (dпл=44мм, dш=22мм, Lш=2000 м, ρш=7800кг/м3, ρж=900 кг/м3).
Масса, связанная с точкой подвеса штанг, также является зависимой от угла поворота кривошипа:
Учет уравновешивания. Влияние того или иного вида уравновешивания на работу СК учитывается следующим образом: · кривошипное уравновешивание: приведенный момент сопротивления
и приведенный момент инерции
· балансирное уравновешивание: приведенный момент сопротивления
· и приведенный момент инерции
где Gур – вес противовесов; mур – масса противовесов; rур – расстояние от оси выходного вала редуктора до центра тяжести установленных противовесов; R2ур – расстояние от точки качания балансира до центра тяжести установленных противовесов.
1. Предложено уточнение Т-образной схемы замещения асинхронного двигателя, позволяющее учесть магнитные потери в роторе машины, что особенно важно для приводов с тяжелыми условиями пуска, к которым, в частности, относятся станки–качалки. Разработаны алгоритмы и программное обеспечение, позволяющие рассчитать параметры уточненной схемы замещения по каталожным данным. 2. Разработана математическая модель механической части привода, позволяющая рассчитывать динамику электромеханических переходных процессов. Все параметры модели могут быть легко определены по справочной литературе. 3. Использование предложенных моделей в практических расчетах показало достаточно высокую степень их адекватности. Например, по результатам моделирования определена мощность резистора динамического торможения для преобразователя частоты VAT2000 30кВт “General Electric”. Справедливость результатов расчетов подтверждена на практике.
Архипов К. И., Попов В. И., Попов И. В., Справочник по станкам-качалкам. – Альметьевск, 2000. Гейлер Г. Б. Основы электропривода. – Минск, 1972. Иванов-Смоленский А. В. Электрические машины. – М., 1980. Ключев В. И. Теория электропривода. – М.: Энергоатомиздат, 1998. Меньшов Б. Г., Ершов М. С., Яризов А. Д. Электротехнические установки и комплексы в нефтегазовой промышленности. – М.: Недра, 2000 Муравьев И. М. Разработка и эксплуатация нефтяных и газовых месторождений. – М.: Недра, 1970. Пискунов Н. С. Дифференциальное и интегральное исчисления. – М.: Наука, 1985.
* Авторы благодарны профессору А.П. Телкову за совместное обсуждение статьи.
* Автор благодарит профессора М.В. Лурье за руководство работой.
* В следующей статье будут рассмотрены технические решения для реализации предложенного способа – использование помехи в качестве несущей.
* Работа выполнялась в рамках программы фундаментальных исследований Отделения ЭММиПУ РАН «Динамика и акустика неоднородных жидкостей, газожидкостных систем и суспензий».
[k1]
|
|||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.009 с.) |

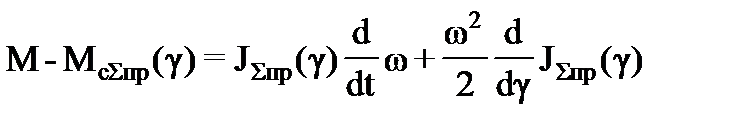 ,
,

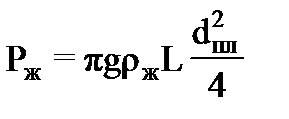 ,
, 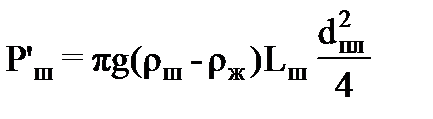 ,
, 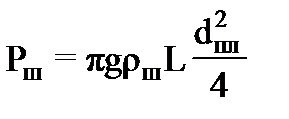 ,
,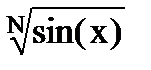 ,
,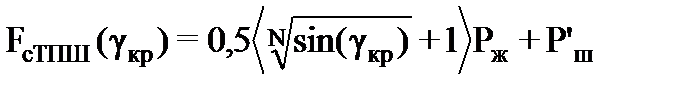 .
.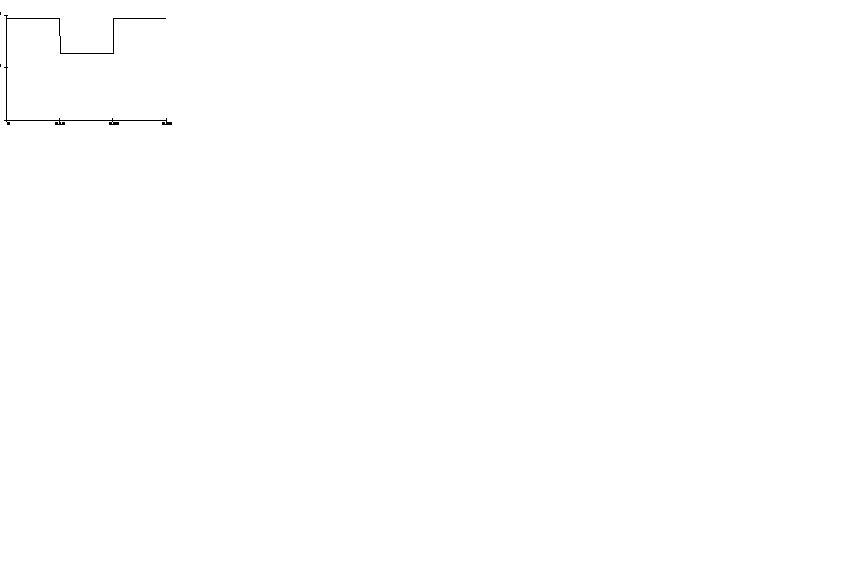
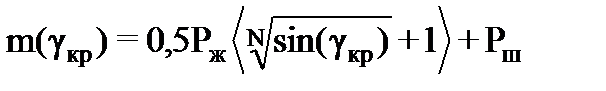 .
.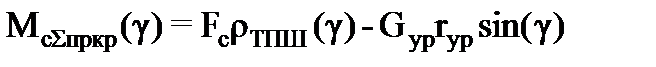
 ;
;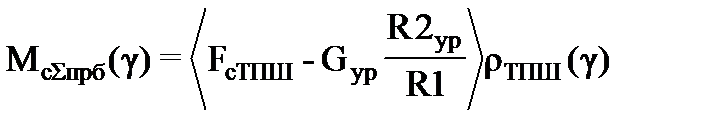
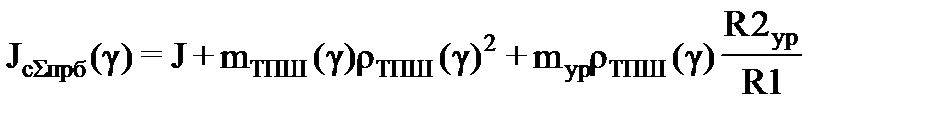 ,
,


