Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И применение его в трубопроводном транспорте нефтиСодержание книги
Поиск на нашем сайте
ри течении жидкости в цилиндрическом канале возможны два режима: ламинарный или турбулентный. При малых скоростях течения реализуется ламинарный режим, для которого коэффициент гидравлического сопротивления рассчитывается по формуле λлам = 64 / Re. С увеличением скорости течения и сопутствующем росте числа Рейнольдса происходит переход от упорядоченного ламинарного течения к хаотичному турбулентному в диапазоне чисел Re = 2000 ÷ 3000. Турбулизация потока сопровождается ростом коэффициента гидравлического сопротивления, изменение которого в области гидравлически гладких труб (3000 < Re < 50000) описывается эмпирическим уравнением Блазиуса λтурб..= 0,3164/Re0,25. При подстановке значений λлам или λтурб в обобщенное уравнение Дарси-Вейсбаха преобразуется в формулу Пуазейля (1а) или в выражение (1б), позволяющие рассчитывать объемные расходы низкомолекулярных (ньютоновских) жидкостей при ламинарном и турбулентном режимах: где Q = π R 2 · U – объёмный расход; U – среднерасходная скорость; ΔР = Рнач. – Ркон . – потери давления на трение в трубе длины L и радиуса R; ρ – плотность жидкости; η и ν = η/ρ – динамическая и кинематическая вязкости соответственно. Анализ уравнений (1а) и (1б) показывает, что турбулентный режим является более энергоемким, так как показатель степени при перепаде давления в (1б) меньше единицы. Из этих уравнений также следует, что независимо от режима течения объёмная скорость должна уменьшаться с ростом вязкости жидкости. Для увеличения пропускной способности нефтепроводов и снижения энергетических затрат на перемещение единицы объема жидкости, как правило, используют традиционные пути уменьшения вязкости: подогрев, разбавление маловязким растворителем и введение депрессорных присадок [1]. Вышеперечисленные методы эффективны для ламинарного режима течения, при котором объемный расход обратно пропорционален вязкости (формула 1а). В большинстве случаев при перекачке нефти и нефтепродуктов по трубопроводам реализуется турбулентный режим течения, объемный расход, при котором слабо зависит от вязкости формула (1б). Например, двукратное уменьшение вязкости при ламинарном режиме приводит к увеличению объёмной скорости также в два раза, а при турбулентном режиме такое же уменьшение вязкости сопровождается ростом скорости всего на 10 %. Поэтому в последнее время все чаще применяются энергосберегающие технологии трубопроводного транспорта с использованием противотурбулентных присадок. В настоящее время почти 20% всей сырой нефти, перекачиваемой по трубопроводам США, содержат антитурбулентные добавки, а география их применения включает также нефтедобывающие регионы Мексики, Венесуэлы, Норвегии и страны Ближнего Востока [2]. Введение полимера в турбулентный поток приводит к частичной ламинаризации течения [3] и, как следствие этого, к уменьшению коэффициента гидравлического сопротивления полимерного раствора (λР) по сравнению с коэффициентом чистого растворителя (λ S). Уменьшение коэффициента сопротивления сопровождается в соответствии с уравнением (1) либо уменьшением потерь на трение при фиксированном объёмном расходе, либо увеличением объёмной скорости течения при постоянном перепаде давления. Количественные значения λ P при числах Re > 2000 попадают в область, сверху ограниченную кривой Блазиуса (рис.1), а снизу – гипотетическим продолжением кривой ламинарного течения, то есть для коэффициентов сопротивления полимерных растворов выполняется условие 64/Re < λ P < 0,3164/Re0,25. Чем выше относительная молекулярная масса полимерного образца (Mr) и чем больше его концентрация (С), тем ближе значение λ p к кривой ламинарного течения и тем больше разница Δλ = λS - λP. Количественно величину эффекта Томса (DR) принято оценивать по относительному изменению коэффициента гидравлического сопротивления, выраженному в процентах: где λS = λ турб – коэффициент гидравлического сопротивления чистого растворителя; λP – коэффициент гидравлического сопротивления полимерного раствора. Максимально возможный эффект будет наблюдаться при полной ламинаризации потока, то есть при λ Р = λ лам. В этом предельном случае:
Таким образом, можно прогнозировать, что в идеальных условиях самая эффективная добавка, введенная в оптимальном количестве, не проявит эффекта, превышающего рассчитанного по формуле (3). Результаты экспериментального тестирования антитурбулентной эффективности некоторых систем полимер-растворитель, проведенные на лабораторном турбулентном реометре, представлены на рис. 1. Турбулентный реометр конструктивно подобен капиллярному вискозиметру, но в нем имеется возможность задавать различные перепады давления в цилиндрическом канале, что позволяет проводить исследования в широком диапазоне чисел Рейнольдса, охватывающем ламинарную и турбулентную области. Устройство турбореометра более подробно описано в работе [4]. Измеряемыми величинами при пропускании жидкости через канал турбореометра являются объёмный расход и перепад давления. После подстановки в формулу (2) значений λs и λp из уравнения Дарси-Вейсбаха (1) получим выражение (4), позволяющее по экспериментально измеряемым величинам перепада давления и объёмного расхода, рассчитывать величину эффекта Томса:
В лабораторных экспериментах или в процессе эксплуатации трубопроводов возможны два предельных варианта: · в случае перекачки чистой нефти и нефти с полимерной добавкой насосами объемного действия (поршневыми или шестеренчатыми) при QS = QP = const эффект будет равен
· снижение давления в магистральном трубопроводе без потери его производительности целесообразно в двух случаях: при эксплуатации старых трубопроводов для уменьшения вероятности возникновения аварийной ситуации и для подкачки нефти из подводящих трубопроводов, снабженных маломощными насосами, не способными нагнетать на высокое противодавление магистрального нефтепровода; · в случае перекачки чистой нефти и нефти с полимерной добавкой под действием постоянного перепада давления, то есть при Δ PS =Δ PP = const имеем
l тур =0,3164 (С = 100 г/м3; Mr = 0,5×106)
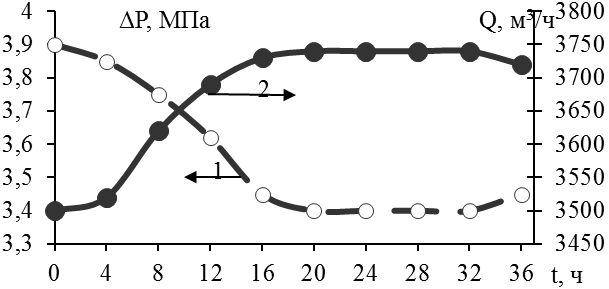
В литературных источниках [5, 6], посвященных эффекту Томса, описаны гидродинамические свойства десятков эффективных в лабораторных условиях противотурбулентных добавок, но не все они при введении в промышленные трубопроводы оказались способными снижать сопротивление. Это расхождение между обнадеживающими результатами лабораторных экспериментов и отрицательными итогами натурных испытаний объясняется тем, что в большинстве случаев, изучая поведение полимерных растворов, исследователи стремились смоделировать на лабораторных стендах течения с числами Рейнольдса, идентичными существующим в реальных трубопроводах, упуская при этом величину напряжения сдвига на стенке трубы (t w). Между этими важнейшими гидродинамическими параметрами турбулентного течения, а также диаметром трубы (D), плотностью (p) и кинематической вязкостью (ν) жидкости существует функциональная связь: Из уравнения (7) следует, что для осуществления течения жидкости с фиксированными вязкостью и плотностью при некоторой заданной величине Re = const в трубках малого диаметра лабораторных установок необходимо приложить значительно бóльшие напряжения сдвига (на несколько порядков), чем в магистральных трубопроводах для достижения того же значения числа Рейнольдса. Например [7], в магистральном трубопроводе Александровское – Анжеро-Судженск с диаметром 1,2 м перекачивается нефть с кинематической вязкостью 5·10-6 м2/с и плотностью 850 кг/м3 при напряжении сдвига 3 Па, что соответствует турбулентному режиму с числом Re = 350·103. Чтобы в турбулентном реометре с диаметром трубки 2·10–3 м создать течение нефти с таким же числом Рейнольдса, необходимо приложить напряжение сдвига tw= 1·106 Па, то есть на шесть порядков более высокое. Такие напряжения сдвига почти трудноосуществимы в лабораторных условиях, так как для этого в трубке лабораторного реометра длиной 1 м нужно создать перепад давления ∆P = 200 МПа. Экспериментально установлено, что при достижении достаточно больших напряжений сдвига способность снижать сопротивление начинают проявлять даже олигомеры. Поэтому, считая наличие турбулентности (Re >2300) необходимым условием проявления эффекта Томса, количественному значению числа Рейнольдса мы отводим второстепенную роль, принимая за доминанту величину напряжения сдвига на стенке трубы, которая в лабораторных экспериментах должна быть равной существующим в магистральных нефтепроводах. Теоретическим обоснованием такого подхода нам послужило уравнение [8, 9], связывающее величину приращения объемного расхода с гидродинамическими параметрами течения и физико-химическими характеристиками полимерных растворов: где Δ Q = Q Р – QS – приращение объемного расхода полимерного раствора по сравнению с растворителем; S = πּ R 2 – площадь поперечного сечения цилиндрического канала; Из полученного нами уравнения (8) видно, что приращение объёмного расхода (ΔQ) полимерного раствора по сравнению с расходом чистого растворителя в явном виде зависит от напряжения сдвига на стенке трубы, а зависимость от числа Рейнольдса может быть представлена опосредовано с использованием уравнения (7). Из уравнения (8) также следует, что эффект Томса проявляется (ΔQ > 0) при положительном значении алгебраической суммы в квадратных скобках, то есть при выполнении следующего условия: Приравняв к единице левую часть неравенства (9), можно рассчитать «пороговое» напряжение сдвига τпор = RT /[ η ]· M, то есть минимальное напряжение, начиная с которого скорость турбулентного течения полимерного раствора становится больше скорости течения чистого растворителя. Анализ неравенства (9) показывает, что полимерный образец является эффективным [η] · M · τw/ RT > 1 при тем меньших напряжениях сдвига, чем больше характеристическая вязкость и молекулярная масса полимера, а также, чем меньше температура. В промышленных нефте- и продуктопроводах величины напряжения сдвига, как правило, имеют невысокие значения в интервале от 1 до 10 Па, поэтому эффективным оказываются полимеры сверхвысокой молярной массы (М >103 кг/моль) и большой характеристической вязкости ([η] >1 м3/кг). Таким образом, если известны М и [η] полимерного образца, а также температура раствора и напряжение сдвига на стенке конкретного трубопровода, то при выполнении неравенства (9) можно теоретически прогнозировать положительный результат от применения полимерной добавки. В обратном случае применение полимера бесперспективно. Если же численные значения М и [η] неизвестны, можно провести экспериментальное тестирование полимерных растворов на лабораторном турбулентном реометре при двух (необходимом и достаточном) условиях: · необходимым условием является создание в лабораторном реометре турбулентного режима течения с Re > 2300; · достаточным условием может считаться наличие положительного результата (ΔQ > 0) лабораторных экспериментов при напряжениях сдвига в реометре (τлаб) равном существующему в конкретном трубопроводе (τтр), то есть при τлаб = τтр; на лабораторном турбореометре необходимо измерить объёмные расходы чистого растворителя (Q S) и ряда полимерных растворов различных концентраций (QР) при напряжении сдвига, равном имеющемуся в промышленном трубопроводе (τлаб = τтр). Используя формулы (2 и 4), рассчитаем значения DR, соответствующие определенным концентрациям растворов. Строим калибровочную графическую зависимость величины эффекта от содержания полимера в растворе, по которой можно будет прогнозировать величину эффекта в промышленном трубопроводе. Экономически целесообразным является использование полимерных образцов, максимальные значения эффекта Томса на концентрационных кривых не превышают 50 г/м3. Нефти являются многокомпонентными системами, растворяющая способность которых определяется относительным содержанием в них предельных, циклических и ароматических углеводородов, а также наличием полярных соединений, содержащих гетероатомы в структуре. Поэтому подбор противотурбулентных добавок необходимо вести с учетом химической природы конкретной нефти. В лабораторных условиях нами протестированы различные полимеры (полиизопрен, полибутадиен, полистирол, полиалкилакрилаты и др.). Наиболее универсальными и эффективными оказались высшие рентгеноаморфные поли-α-олефины, которые нашли практическое применение в трубопроводном транспорте нефти. Положительные результаты лабораторного тестирования по описанной выше методике образцов поли-α-олефинов, синтезированных на промышленных мощностях Томского нефтехимического комбината, позволили применить их в магистральных нефтепроводах Александровское – Анжеро-Судженск и Тихорецк – Новороссийск [10, 11]. Например, в процессе дозирования полимерной добавки в трубопровод Тихорецк – Новороссийск потери давления на трение снижены от 3,9 до 3,3 МПа и одновременно увеличен расход нефти от 3500 до 3740 м3/ч (рис. 2).
В результате проведенного натурного эксперимента на трубопроводе Тихорецк – Новороссийск [11] гидродинамическое сопротивление снижено на DR = 23% при введении в трубу полимера в концентрации 7 г/м3. Сравним полученный результат с данными по использованию противотурбулентной добавки CDR-102 на Трансаляскинском трубопроводе [12] (таблица).
Вывод Производимая на Томском нефтехимическом комбинате отечественная антитурбулентная добавка по технологическим качествам не уступает импортным аналогам.
1. Алиев Р.А, Белоусов В.Д, Немудров А.Г, Юфин В.А, Яковлев Е.И. Трубопроводный транспорт нефти и газа.–М.: Недра, 1988.- 368 с. 2. Мастобаев Б.Н., Шаммазов А.М., Мовсумзаде Э.М. Химические средства и технологии в трубопроводном транспорте нефти. - М.: Химия. - 2002.- 295 с. 3. Toms B. A. Some Observations on the Flow of Linear Polymer Solutions Through Straight Tubes at Large Reynolds Numbers / Proceeding International Congress on Rheology. Vol. 2. North Holland Publishing Co. Amsterdam. 1949.- P. 135. 4. Малкин А. Я., Несын Г. В., Манжай В. Н., Илюшников А. В. Новый метод реокинетических исследований, основанный на использовании эффекта Томса // Высокомолекулярные соединения. 2000.- Т.42, №2. - С.377 - 384. 5. Virk P.S. Drag Reduction Fundamentals // AJChE Journal.-1975. V.21, №4. - Р. 625 - 246. 6. Белоусов Ю.П. Противотурбулентные присадки для углеводородных жидкостей.-Наука, 1986.- 144с. 7. Манжай В.Н., Илюшников А.В., Гареев М.М., Несын Г.В. Лабораторные исследования и промышленные испытания полимерной добавки для снижения энергетических затрат на магистральном нефтепроводе // Инженерно-физический журнал.–1993. Т.65, №5. - С.515-517. 8. Манжай В.Н. Турбулентное течение разбавленных растворов полимеров в цилиндрическом канале // Теоретические и прикладные основы физико-химического регулирования свойств нефтяных дисперсных систем. Томск: Томский государственный университет. 2001. Часть 3. - С.71-81. 9. Манжай В.Н., Ечевская Л.Г., Илюшников А.В. и др. Исследование противотурбулентной эффективности высших полиолефинов и тройных сополимеров олефинов //Журнал прикладной химии. 2004. Т.77, №3.- С.456 - 460. 10. Гареев М.М., Несын Г.В., Манжай В.Н. Результаты введения в поток нефти присадки для снижения гидродинамического сопротивления //Нефтяное хозяйство. 1992, № 10. - С.30. 11. Несын Г.В., Манжай В.Н., Попов Е.А. и др. Эксперимент по снижению гидравлического сопротивления нефти на магистральном трубопроводе Тихорецк – Новороссийск. // Трубопроводный транспорт. 1993. № 4.- С.28-30. 12. Beaty W.R. and oth. New high-performance flow improver offers alternatives to pipeliners // Oil and Gas Journal. 1982. V.80, №32. - P.96 -102.
(12) Тема 2006-3-44 С. Оценка погрешности измерения с помощью датчиков деформаций интегрального типа. Сызранцев В.Н., Голофаст С.Л., Богомолов О.В. Оценка погрешности измерения с помощью датчиков деформаций интегрального типа крутящего момента на валах и роторах / Известия высших учебных заведений. Нефть и газ. 2006, № 3, С. 44 – 49 УДК 539. 3/.6/622. 243. 56
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.009 с.) |

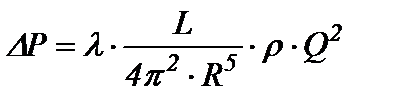 (1)
(1)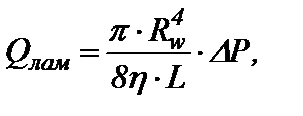 (1а)
(1а)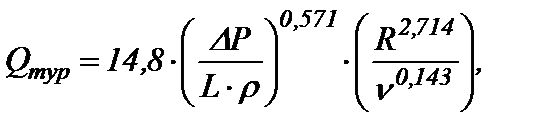 (1б)
(1б)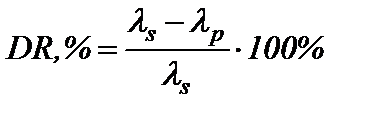 , (2)
, (2)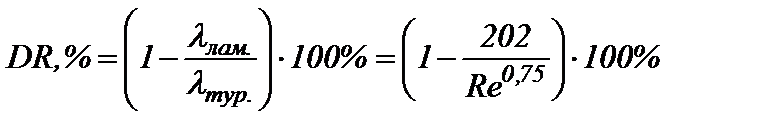 . (3)
. (3)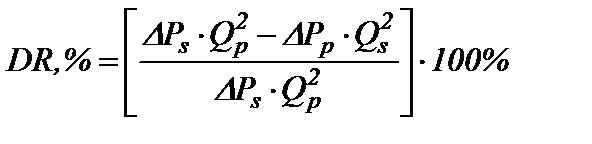 . (4)
. (4)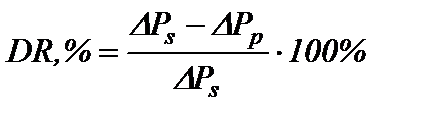 , а применение полимерной добавки приведет к снижению потерь давления на трение до значения
, а применение полимерной добавки приведет к снижению потерь давления на трение до значения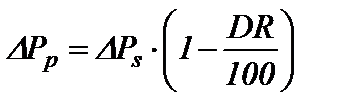 ; (5)
; (5)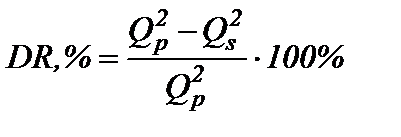 и, следовательно, возросший расход нефти может быть рассчитан по формуле
и, следовательно, возросший расход нефти может быть рассчитан по формуле 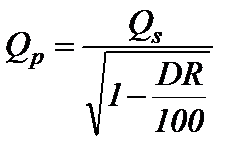 . (6)
. (6)
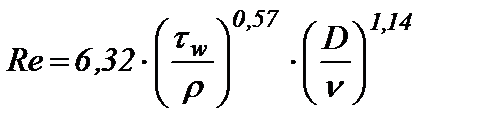 . (7)
. (7)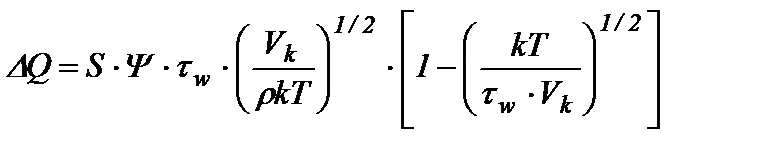 , (8)
, (8)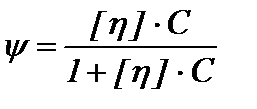 – объемная доля макромолекулярных клубков в растворе, зависящая от характеристической вязкости [ η ] и концентрации полимерного раствора (C);
– объемная доля макромолекулярных клубков в растворе, зависящая от характеристической вязкости [ η ] и концентрации полимерного раствора (C); 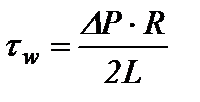 – напряжение сдвига на стенке трубы радиуса (R) и длины (L) при заданном перепаде давления (ΔP);
– напряжение сдвига на стенке трубы радиуса (R) и длины (L) при заданном перепаде давления (ΔP); 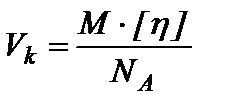 – объем макромолекулярного клубка с иммобилизованным растворителем, зависящий от молярной массы полимерного образца (М) и характеристической вязкости его растворов [η]; ρ - плотность растворителя; k – постоянная Больцмана; Т – температура.
– объем макромолекулярного клубка с иммобилизованным растворителем, зависящий от молярной массы полимерного образца (М) и характеристической вязкости его растворов [η]; ρ - плотность растворителя; k – постоянная Больцмана; Т – температура.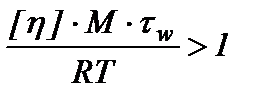 . (9)
. (9)