
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Mathematical modeling, combustion products, dust-laden gas, filtrationСодержание книги
Поиск на нашем сайте
Mathematical modeling of fuel combustion products filtration processes. Borzykh V.E., Semyonov B.V. Two approaches are reviewed for mathematical modeling of petrol fuel combustion products filtration in SVS-elements. One approach relates to a problem of viscous incompressible fluid flow which is described by Navie-Stocks equations, and another one relates to the model of dust-laden gas. The advantage of the last approach is in its capability to help to develop a common approach permitting to describe the transfer and diffusion processes in all their diversity basing on common grounds and to perform a numerical experiment. Ref. 3.
овременные масштабы развития производства непрерывно связаны с интенсивным использованием автотранспорта. Степень их воздействия на окружающую среду многогранна, в значительной мере связана с выбросом вредных веществ отработавших газов (ОГ) в атмосферу. Снижение выбросов загрязняющих веществ до норм «Евро» (эти требования вступили в силу в 2006 году) может быть обеспечено различными путями. Наибольшую техническую целесообразность имеет каталитическая нейтрализация ОГ. Снижение выбросов загрязняющих веществ до требуемого уровня смогут обеспечить фильтры-нейтрализаторы, изготовленные по современной технологии – самораспространяющийся высокотемпературный синтез (СВС) конденсированных смесей, не содержащих благородных металлов в режиме электротеплового взрыва (ЭТВ). Несмотря на широкую распространённость пористых сред, существует ряд нерешённых задач, в частности, при описании процессов фильтрации отработанных газов в фильтроэлементах выпускных систем двигателей внутреннего сгорания. Математическое моделирование этих процессов позволит провести их детальный анализ, изучить влияние параметров пористой среды на ход процесса переноса. Выразить математически фильтрационный или диффузионный поток так, чтобы формулы отражали реальное перемещение частиц по поровому пространству, крайне затруднительно. Как правило, в прикладных исследованиях основной интерес представляют макроскопические особенности того или иного процесса переноса. Микроскопические детали интересны лишь в той мере, в которой они способны повлиять на процесс. С этой точки зрения формулы описывают процессы переноса как единое движение фиктивной сплошной среды через некоторое пространство, занимаемое в действительности пористой средой. Подобная идеализация весьма плодотворна, так как благодаря простоте математической записи она представляет очень широкие возможности для моделирования разнообразных ситуаций. Для описания процессов переноса в пористых средах существует ряд методов, характеризующих процессы течения газа и жидкости в пористых средах, одним из таких можно считать задачу о течении вязкой несжимаемой жидкости, описываемую уравнениями Навье-Стокса(макроскопический подход). Рассмотрим один из подходов численной реализации решения данной задачи [2]:
Криволинейная граница порового канала описывается следующей функцией:
Для данной задачи могут быть поставлены следующие краевые условия. На входе канала х = 0 задан параболический профиль продольной составляющей скорости и нулевое значение поперечной составляющей:
На верхней стенке у = Г(х) заданы условия, следующие из условий прилипания и непротекания:
Нижняя граница у = 0 является линией симметрии:
На выходе канала х =R для продольной составляющей скорости задано однородное краевое условие второго рода, для поперечной составляющей – нулевое значение:
Для численной реализации рассмотренной задачи можно использовать следующий подход: · дискретизация производных конечными разностями на равномерных декартовых сетках; · независимость формы записи линейных соотношений, аппроксимирующих краевые условия от вида уравнений для внутренних точек области. Из вышерассмотренного подхода ясно, что он требует подробного описания геометрии поровых каналов, краевых и граничных условий, что почти невозможно для решения задачи фильтрации отработанных газов через фильтроэлемент со сложной внутренней геометрией. Поэтому рассмотрим другой подход – молекулярно-кинетический [3], описывающий процессы переноса в пористых средах: модель запылённого газа. В нём обосновывается аддитивность вязкого и диффузионного потоков, используется весь аппарат кинетической теории Чепмена – Энскога для смеси газов, в которой пористая среда рассматривается как один из компонентов смеси. В этом подходе изменение давления можно формально описать через изменение мольной доли "пылевого" компонента. Главное достоинство этой модели состоит в том, что она обеспечивает возможность разработки общего подхода, позволяющего с единых позиций, основанных на прочном теоретическом базисе, описать процессы переноса и диффузии во всем их разнообразии. Она позволяет использовать все достижения современной кинетической теории газов в совершенно новом контексте без специального повторения решения Чепмена - Энскога. Термодиффузия, бародиффузия и силовая диффузия легко могут быть описаны в рамках модели. В этой теории легко устанавливаются многие особенности в зависимостях коэффициентов диффузии от давления и состава. Часто в этой модели можно выявить определенную взаимосвязь между различными явлениями, на основе строгого математического подхода без обращения к деталям разработанного ранее аппарата кинетической теории. В основе теории лежит утверждение о том, что перенос газа в пористом теле (или в капилляре) осуществляется следующими тремя независимыми механизмами: · свободно-молекулярное или кнудсеновское течение, реализующееся при столь малой плотности газа, что частотой столкновений между молекулами можно пренебречь по сравнению с частотой их столкновений с поверхностями каналов пористого тела или капилляра; · вязкое течение, при котором газ течет как сплошная среда под действием градиента давления и межмолекулярные столкновения преобладают над столкновениями молекул с поверхностью. Этот механизм иногда называют также конвективным или переносом газа как целого; · диффузия в режиме сплошной среды, когда отдельные компоненты смеси перемещаются относительно друг друга под действием градиента концентрации (обычная диффузия), градиента температуры (ермодиффузия) или внешних сил (силовая диффузия). Здесь снова межмолекулярные столкновения происходят чаще, чем столкновения молекул с поверхностью; · в приведенной классификации, очевидно, не учтен еще один механизм переноса газа, имеющий в некоторых случаях не меньшую практическую значимость, а именно: · поверхностная диффузия, при которой молекулы газа перемещаются вдоль поверхности твердого тела, не покидая адсорбционного слоя. Будем предполагать, что механизм 4 никак не связан с механизмами 1 – 3. На первом этапе не будем рассматривать этот механизм, а в дальнейшем просто укажем, как он может быть включен в общую расчетную схему. Физическую сущность модели определяет запыленный газ, в котором частицы пыли образуют пористую среду. Частицы пыли рассматриваются как один из компонентов газовой смеси, состоящий из больших тяжелых неподвижных молекул, равномерно распределенных в пространстве. Если в газе имеется градиент давления, то для обеспечения неподвижности частиц пыли к ним необходимо приложить некоторую внешнюю силу. Для математической формулировки модели не нужно знать истинную природу этой внешней силы; в экспериментах внешняя сила обычно бывает обусловлена каким-либо креплением, обеспечивающим неподвижность пористого тела. Классическая кинетическая теория газов имеет дело только с упругими столкновениями, внутренние степени свободы многоатомных молекул в расчет не принимаются. Обобщенные теории, учитывающие внутренние степени свободы, в первом приближении приводят к уравнениям переноса, по внешнему виду сходным с соответствующими уравнениями для одноатомных газов. Различаются только выражения для кинетических коэффициентов, которые для многоатомных газов более сложны и содержат члены, связанные с учетом неупругих столкновений. Таким образом, полученные в рамках модели запыленного газа общие соотношения после соответствующей замены явных выражений для кинетических коэффициентов применимы к одноатомным и многоатомным газам. Рассмотрим уравнения диффузии и уравнения вязкого переноса. Уравнения диффузии для многокомпонентной смеси v компонентов выглядят следующим образом:
где градиентный член di равен
средняя молекулярная масса смесиопределяется равенством
и Fi –внешняя сила, действующая на молекулы i -го компонента. Четыре слагаемых в правой части равенства (9) описывают соответственно обычную диффузию, бародиффузию, силовую диффузию и термодиффузию. Заметим, что равенство (8) представляет i -е уравнение системы v уравнений, из которых только v -1 уравнений являются независимыми (любое из v уравнений системы равно сумме остальных v -1 уравнений). Уравнения диффузии в форме (8) и (9) могли бы быть получены и из соображений о переносе импульса, но для нахождения явных выражений для кинетических коэффициентов Dij и Метод Чепмена – Энскога позволяет рассчитать вязкость простого газа или газовой смеси, выразив ее через характеристики молекул. Иначе говоря, чепмен-энскоговское выражение для тензора напряжений дает для вязкого потока тот же самый результат:
где
где | Н | – детерминант, элементы которого даются выражениями:
Написанные матричные элементы, как и в случае теплопроводности, получены лишь в первом приближении теории и дают очень точный результат, если в качестве Осуществим приближение к модели запыленного газа, наложив шесть дополнительных условий. 1. Будем считать В o характеристикой геометрических свойств пористой среды; В o можно рассчитать независимо или определить экспериментально. Аналогичным образом вводится эффективный коэффициент диффузии: 2. Предположим, что частицы пыли неподвижны и равномерно распределены в пространстве. Отсюда следует, что в уравнениях (8) и (9) имеем Jd = 0 и 3. Поскольку частицы пыли неподвижны, они не вносят непосредственного вклада в λ и ηв любой из формул для смеси. 4. Величины n и р, входящие в различные слагаемые уравнений диффузии, не являются истинными плотностью числа частиц и давлением газа, а содержат вклад от частиц пыли. Обозначать штрихом величины, представляющие вклад от частиц пыли, и опускать штрих, если они учитывают вклад только от истинных молекул, в соответствии со сказанным напишем
Из кинетической теории следует n ' D Более сложно выглядит аналогичный результат для 5. Частицы пыли удерживаются в равновесии внешней силой, компенсирующей любой градиент давления в газе. 6. Величины nDid и В рассмотренной модели запыленного газа пористая среда характеризуется тремя основными параметрами – кнудсеновским коэффициентом проницаемости Кo, параметром вязкого течения B0 и фактором пористости-извилистости Рассмотрим пористую среду в виде набора непересекающихся цилиндрических капилляров радиусом r и длиной Leff. Примем, что каждая пора заканчивается отверстием площадью
Очевидно, что извилистость q связана каким-то образом с отношением Leff / L. Для нахождения этой взаимосвязи рассчитаем величину BO, равную для одного капилляра r 2 /8. Плотность потока при вязком течении дается выражением (11); отнесенное к единице внешней поверхности, это выражение принимает вид
Здесь
Используя выражение (17) для ε, находим
Отметим, что Аналогичные расчеты дают для кнудсеновского течения:
для диффузионного переноса: Получаем
откуда следует, что величину Соотношения, могут оказаться очень полезными, когда не требуется высокой точности расчетов. Для повышения точности существуют различные способы усовершенствования равенства (23). Среди них отметим следующие: 1) пересчет К O с учетом кнудсеновского минимума проницаемости; 2) внесение поправок на отличие сечения капилляров от кругового и на изгибы в порах; 3) внесение поправок на распределение пор по размерам. Рассмотрим эти поправки по порядку. Равенство KO = r /2 для прямолинейного цилиндрического капилляра справедливо только в пределе свободно-молекулярного течения в условиях диффузного рассеяния молекул поверхностью стенок капилляра. Экстраполяция измеренной при более высоких давлениях проницаемости на предельную точку нулевого давления дает для К O более низкое значение, которое соответствует скорее первому приближению для коэффициента кнудсеновской диффузии, чем его истинному значению. Неоднородная пористость не вызывает особых затруднений, пока уравнения переноса остаются линейными после интегрирования (все дифференциальные уравнения переноса, безусловно, являются линейными). Неоднородность сказывается только на параметрах KO, В0 и Если имеются другие внешние силы (нестационарное течение газа), то добавляем следующее уравнение баланса сил:
При наличии внешних сил должно быть изменено и уравнение вязкого течения, и при выполнении соотношения (24) получаем
Прежде чем рассматривать явный вид выражений nDid и а id, запишем полный набор уравнений переноса. После некоторых преобразований приходим к следующему результату (i, j
где суммирование по j не учитывает пылевой компонент. Коэффициент кнудсеновской диффузии[
На этом завершим описание математической модели запыленного газа, нам остается только с помощью чисто математических преобразований получить явные соотношения, относящиеся к конкретному процессу фильтрации продуктов сгорания бензиновых топлив через фильтроэлемент, полученный по технологии самораспространяющегося высокотемпературного синтеза (СВС). Он позволяет создавать материалы с различными свойствами. В этой связи для проверки описанной математической модели особый интерес приобретает карбид титана. В условиях работы фильтров катализаторы из Ti не подвергаются блокированию пор материала фильтров продуктами загрязнений, ограничивая доступ ких поверхности. Титан в различном сочетании с другими металлами и неметаллами способен нейтрализовать оксиды углерода, углеводороды и окислы азота в потоке газов. Действие его зависит от структуры и удельной поверхности, которые формируются в зависимости от способа приготовления образца. Это объясняется тем, что в присутствии титана образцы имеют большое количество пор, лучшую их конфигурацию, повышенную катионную активность своих элементов. К тому же карбиды тугоплавких металлов WC и TiC являются сравнительно дешевыми и доступными. Титан способствует более полной очистке газов от ВВ, особенно при высоких температурах (выше 700 °С). Присутствие же в порошке титана ионов железа даже при наличии в ОГ сернистых соединений и паров воды обеспечивает 98 % превращения окиси азота в потоке газа. Поскольку железо менее дефицитно, чем медь и тем более драгоценные металлы (платина, родий, рений, палладий), то катализатор на основе титана с примесями железа более коммерчески привлекателен. Вывод Проверку математической модели процесса фильтрации необходимо провести с помощью численного эксперимента на основе фильтроэлемента, полученного по СВС технологии.
1. Борзых В.Э. Очистка отработанных газов ДВС СВС-элементами /В.Э. Борзых, В.Д. Исаенко, П.В. Исаенко/ Транспортные системы Сибири; материалы Всероссийской научно-технической конференции. – Красноярск: ИПЦ КГТУ, 2003. 2. Васильцов ГЛ., Крюков И.А. Численный метод решения уравнений Навье-Стокса, описывающих течения несжимаемой вязкой жидкости, на криволинейной сетке. // Институт проблем механики РАН. Препринт № 594, – Москва, 1997. 3. Мейсон Э., Малинаускас А.. Перенос в пористых средах: модель запыленного газа. – М.: Мир, 1986-200с.
Сведения об авторах
Борзых В.Э., д.ф.-м.н., профессор, заведующий кафедрой «Автоматизация и вычислительная техника, Тюменский государственный нефтегазовый университет, тел.: (3452)280678, borzykh@tsogu.ru Семёнов Б.В., аспирант, Тюменский государственный нефтегазовый университет, тел.: (3452)280678 Borzykh V.E., PhD, professor, Head of Department “Automation and Computing Engineering’, Tyumen State Oil and Gas University, phone: (3452)280678, borzykh@tsogu.ru Semyonov B.V., postgraduate student, Tyumen State Oil and Gas University, phone: (3452)280678
(6) Тема 2009-4-88 ДП. Математическое моделирование изменения приёмистости скважины. Медведский Р.И., Изотов А.А. Изменение приёмистости скважины при загрязнении призабойной зоны // Известия высших учебных заведений. Нефть и газ. 2009. № 4. С. 88 – 92
УДК 533.624
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.012 с.) |

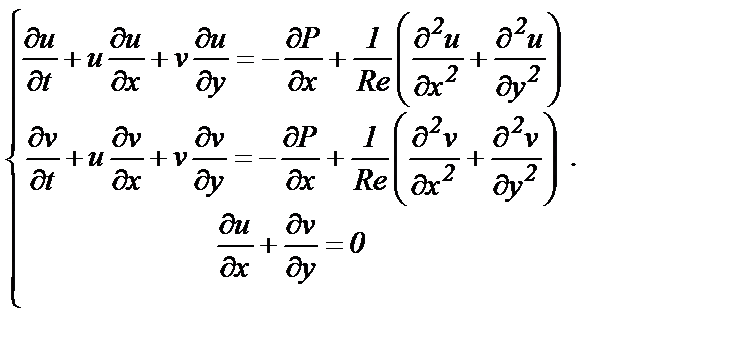 (1)
(1)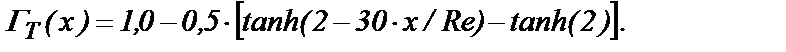 (2)
(2)
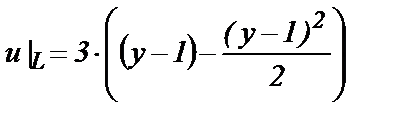 , (3)
, (3)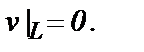 (4)
(4)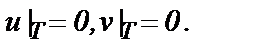 (5)
(5)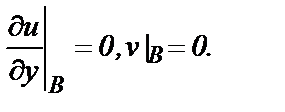 (6)
(6)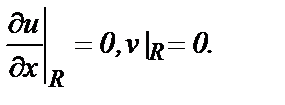 (7)
(7)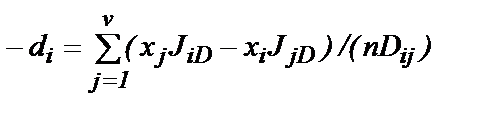 , (8)
, (8)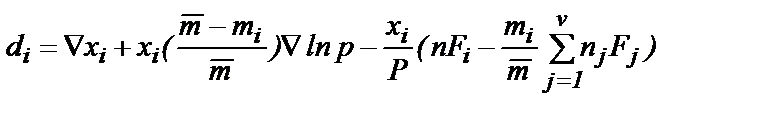
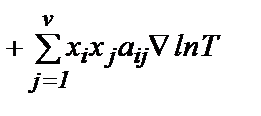 , (9)
, (9)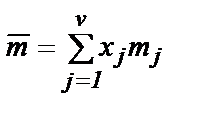 (10)
(10)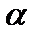 ij требуется привлечение более детальных теоретических методов. Перейдем теперь к рассмотрению уравнений вязкого переноса, а затем обобщим приближение запыленного газа для этих двух наборов уравнений.
ij требуется привлечение более детальных теоретических методов. Перейдем теперь к рассмотрению уравнений вязкого переноса, а затем обобщим приближение запыленного газа для этих двух наборов уравнений.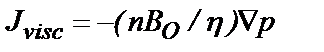 , (11)
, (11)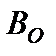 – характеристика геометрии течения. Можно рассчитать парциальнуювязкость
– характеристика геометрии течения. Можно рассчитать парциальнуювязкость 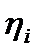 компонента i для смеси, но она в данной задаче не представляет интереса, поскольку в вязком потоке компоненты движутся, не разделяясь. Максимум того, что нам нужно, – это формула для вязкости многокомпонентной смеси. Вид последней схож с выражением для коэффициента поступательной теплопроводности:
компонента i для смеси, но она в данной задаче не представляет интереса, поскольку в вязком потоке компоненты движутся, не разделяясь. Максимум того, что нам нужно, – это формула для вязкости многокомпонентной смеси. Вид последней схож с выражением для коэффициента поступательной теплопроводности: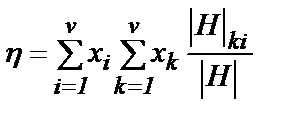 , (12)
, (12)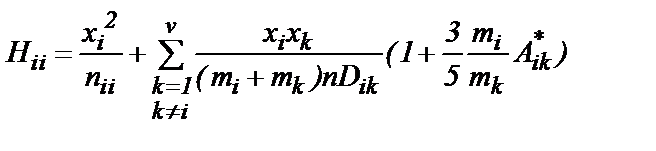 , (13)
, (13)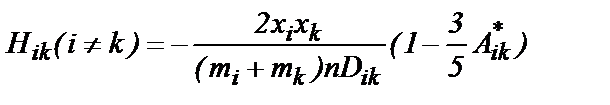 . (14)
. (14)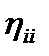 и
и 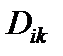 использовать экспериментальные значения. Они пригодны для одноатомных и для многоатомных газов. В последнем случае необходимо только внести незначительные изменения в безразмерные отношения A
использовать экспериментальные значения. Они пригодны для одноатомных и для многоатомных газов. В последнем случае необходимо только внести незначительные изменения в безразмерные отношения A 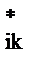 .
.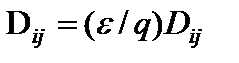 , фактор пористости-извилистости
, фактор пористости-извилистости  считается также характеристикой геометрических свойств среды. Здесь необходимо сделать два замечания. Во-первых, В o и
считается также характеристикой геометрических свойств среды. Здесь необходимо сделать два замечания. Во-первых, В o и 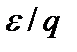 – только локально постоянные параметры, которые могут принимать различные значения в разных точках пористой среды. Во-вторых, Dij можно заменить на D ij только в выражении (8) для плотности потока, но этого нельзя делать в других соотношениях, связывающих Dij с другими кинетическими коэффициентами.
– только локально постоянные параметры, которые могут принимать различные значения в разных точках пористой среды. Во-вторых, Dij можно заменить на D ij только в выражении (8) для плотности потока, но этого нельзя делать в других соотношениях, связывающих Dij с другими кинетическими коэффициентами.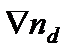 = 0, где индекс относит соответствующие характеристики к пылевому компоненту.
= 0, где индекс относит соответствующие характеристики к пылевому компоненту.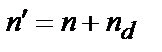 ,
, 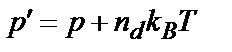 ,
, 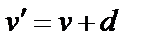 . (15)
. (15)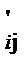 j = nDij. (16)
j = nDij. (16)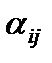 .Он приводит к интересным зависимостям термической транспирации от давления газа.
.Он приводит к интересным зависимостям термической транспирации от давления газа.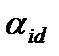 можно выразить через характеристики молекул газа и частиц пыли, непосредственно используя результаты кинетической теории.
можно выразить через характеристики молекул газа и частиц пыли, непосредственно используя результаты кинетической теории.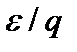 . С практической точки зрения лучше всего определять эти параметры непосредственно из эксперимента. Обычно провести такие эксперименты легче, чем осуществить специальные измерения, требующиеся для получения информации о пористой структуре, необходимой для любых теоретических расчетов.
. С практической точки зрения лучше всего определять эти параметры непосредственно из эксперимента. Обычно провести такие эксперименты легче, чем осуществить специальные измерения, требующиеся для получения информации о пористой структуре, необходимой для любых теоретических расчетов.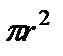 на внешней поверхности блока материала площадью А. Тогда объем пустот в блоке материала, имеющем объем AL, составляет
на внешней поверхности блока материала площадью А. Тогда объем пустот в блоке материала, имеющем объем AL, составляет 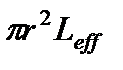 , так что пористость равна
, так что пористость равна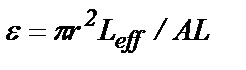 . (17)
. (17)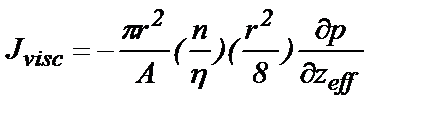 . (18)
. (18)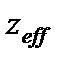 отсчитывается по длине поры. Переходя от
отсчитывается по длине поры. Переходя от 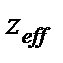 к координате z, отсчитываемой по прямой, которая проходит сквозь пористую среду, получаем
к координате z, отсчитываемой по прямой, которая проходит сквозь пористую среду, получаем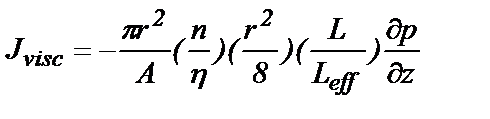 . (19)
. (19)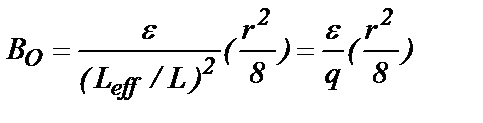 . (20)
. (20)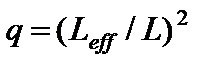 .Вторая степень возникла потому, что отношение
.Вторая степень возникла потому, что отношение 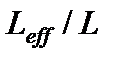 входит в расчеты дважды: один раз в градиентном члене и второй – в объеме пустот.
входит в расчеты дважды: один раз в градиентном члене и второй – в объеме пустот.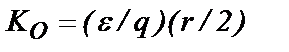 , (21)
, (21)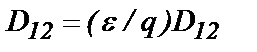 . (22)
. (22)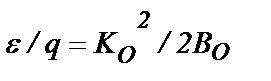 , (23)
, (23)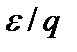 можно найти из измерений только проницаемостей.
можно найти из измерений только проницаемостей. / q,которые следует заменить значениями, усредненными по распределению пор по размерам; сами же уравнения переноса остаются неизменными. Мы рассмотрели уравнения переноса без воздействия внешних сил, то есть стационарный режим течения потока.
/ q,которые следует заменить значениями, усредненными по распределению пор по размерам; сами же уравнения переноса остаются неизменными. Мы рассмотрели уравнения переноса без воздействия внешних сил, то есть стационарный режим течения потока.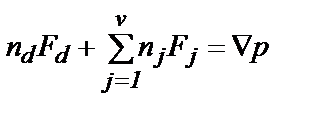 . (24)
. (24)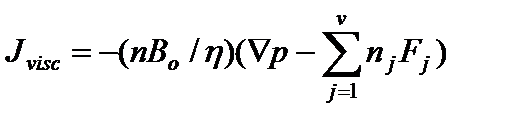 . (25)
. (25)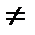 d):
d):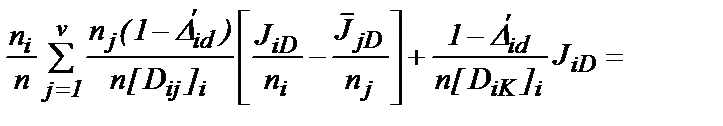
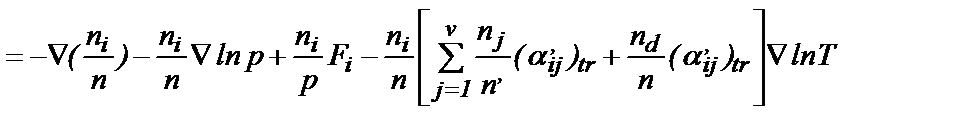 , (26)
, (26)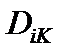 ]1 определяется соотношением
]1 определяется соотношением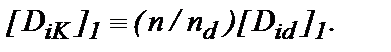 (27)
(27)


