
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растворимость мэ в воде и керосинеСодержание книги
Поиск на нашем сайте
Р – МЭ растворима; НР – МЭ не растворима; Э – МЭ эмульгируется. Остальные обозначения (см.табл. 3).
Сравнительный анализ данных по растворимости в воде и керосине показывает, что до содержания воды в МЭ 20% мас. сохраняется внешняя углеводородная фаза. Это иллюстрируется данными для МР, модифицированных изопропиловым спиртом. МЭ с ИПС растворимы в керосине и одновременно не растворимы в воде – до содержания в них 20 % мас. воды. Для МР, модифицированных ТБС и ЦГС соответствия между растворимостью в воде и керосине нет. Можно предполагать, что здесь также до содержания в МЭ 20 % воды, сохраняется внешняя фаза – углеводородная. Неполная растворимость МЭ с ЦГС и ТБС в керосине, где отмечается хорошая эмульгируемость (см. табл. 4), очевидно, связана с высокой вязкостью таких МЭ. Приведены данные по вязкости (см. рис.3). Отличительной особенностью разработанных МЭ является их «короткая» внешняя углеводородная фаза – всего до 20 % мас. воды. Считается, что для эффективного нефтевытеснения желательно сохранение внешней углеводородной фазы до содержания воды 80 – 90 % мас. Обычно внешнюю углеводородную фазу таких МЭ удлиняют с помощью электролитов. Внешняя водная фаза разработанных микроэмульсий в чистом виде начинается с содержания в них воды 50-60 % мас. Начиная с содержания воды в МЭ 30 % мас., и до содержания воды в МЭ 50-60 % мас., они значительно легче эмульгируются в керосине. Для оценки стабильности МЭ при пониженных температурах в условиях их транспортировки и хранения и для определения возможной инверсии фаз в зависимости от содержания воды в МЭ определялась температура застывания МЭ (ГОСТ 20287-91). Полученные данные (рис.1) показывают, что температура застывания МЭ зависит от природы содетергента (спирта), входящего в состав МЭ и от содержания воды. Наиболее низкие температуры застывания у МЭ, содержащих ИПС. Очевидно, это связано с тем, что ИПС имеет самую низкую собственную температуру плавления (минус 89,5ºС). МЭ, содержащие ЦГС, имеют самые высокие температуры застывания, что связано с его высокой температурой плавления (25,15ºС) и с более высоким его содержанием в МЭ по сравнению с другими содетергентами. МЭ с ТБС по температуре застывания занимают промежуточное положение. В области низких температур можно отметить некоторые особенности поведения МЭ. При содержании воды 10 %, а с ИПС 20 % мас. МЭ имеют низкие температуры застывания. С увеличением содержания воды в МЭ их температуры застывания сначала резко возрастают, затем значительно снижаются с некоторым последующим повышением. Сопоставление данных по температуре застывания МЭ с данными по их растворимости в воде и керосине обнаруживает некоторую корреляцию. Высокие температуры застывания, по нашему мнению, связаны с инверсией (обращение фаз) микроэмульсий - переходом МЭ типа В/М («вода в масле») в МЭ типа М/В («масло в воде»). Необычный процесс застывания наблюдался для МЭ с ЦГС при содержании воды 20%мас. При достижении микроэмульсией температуры 1ºС, несмотря на низкую температуру бани, дальнейшего понижения температуры не происходило. Напротив, через некоторое время происходило самопроизвольное повышение температуры до 2,5ºС. При этом застывание так и не достигалось. При низких температурах застывание всех микроэмульсий при содержании в них воды более 20% мас. сопровождалось образованием кристалликов льда. При низком содержании воды мицеллы типа В/М разрушались с выделением воды и последующей ее кристаллизацией. При высоком содержании воды низкие температуры не оказывали влияния на мицеллы типа М/В и вода кристаллизовалась из внешней фазы. Показатели преломления МЭ в зависимости от содержания в них воды представлены (см. рис.2). На зависимостях Представлены данные зависимости вязкости МЭ при 50ºС от содержания в них воды (см. рис. 3). Характер зависимостей Зависимости Микроэмульсии для нефтевытеснения должны сохранять стабильность в условиях не только низких температур (см. рис. 1), но и пластовых температур Западной Сибири, доходящих 80° С. Дополнительно изучена термостабильность наиболее подходящих для нефтевытеснения микроэмульсий с изопропиловым спиртом. Методика оценки термостабильности заключалась в выдерживании образца микроэмульсии в пределах температур от 30 до 80°С с шагом в 10°. Микроэмульсии считались стабильными, если при времени выдерживания в течение 60 минут визуально сохранялась их фазовая однородность. Фиксировалась критическая температура, при которой происходит появление отделившейся фазы. Исследования показали, что микроэмульсии в изучаемых условиях оставались стабильными. Очевидно, что термостабильность микроэмульсий помимо оптимального компонентного состава, определяется также температурой кипения изопропилового спирта, которая превышает 80°С (см. табл. 1) – температуру пласта.
Выводы
Разработаны мицеллярные растворы и микроэмульсии на основе мыл олеиновой кислоты и полиэтиленполиаминов в керосине, стабилизированные трет-бутиловым, циклогексиловым и изопропиловым спиртами. Изучены физико-химические свойства микроэмульсий. По совокупности физико-химических свойств показано, что внешняя углеводородная фаза микроэмульсий сохраняется до 20-30% мас. содержания воды. Полная инверсия микроэмульсий типа В/М в МЭ М/В происходит при содержании воды более 60% мас. При промежуточном содержании воды микроэмульсии находятся в переходном состоянии. Для нефтевытеснения рекомендованы микроэмульсии, представляющие растворы полиэтиленполиаминных мыл олеиновой кислоты в керосине, стабилизированные изопропиловым спиртом. Рекомендованные мицеллярные растворы характеризуются благоприятной зависимостью вязкости от температуры, низким поверхностным натяжением, хорошими низкотемпературными свойствами, высокой стабильностью.
1. Байков Н.М. Наращивание объемов извлекаемых запасов нефти с помощью методов увеличения нефтеотдачи // Нефтяное хозяйство. – 2004. – № 7. – С. 125. 2. Буклов А.Г. Перспективы новых методов повышения производительности скважин и нефтеотдачи пластов // Нефтепромысловое дело. – 2007. – № 9. – С. 68. 3. Козин В.Г., Башкирцева Н.Ю., Гарипов Р.Н., Хасанов И.Р. Повышение нефтеотдачи пластов с применением мицеллярных растворов с гидрофобизирующей составляющей // Нефтяное хозяйство. – 2004. - № 8. – С. 79. 4. Сургучев М.Л., Шевцов В.А., Сурина В.В. Применение мицеллярных растворов для увеличения нефтеотдачи пластов. - М.: Недра, 1977. – 175 с. 5. Вайсбергер А., Проскауэр Э., Риддик Дж., Тупс Э. Органические растворители. – М: Изд-во Иностранной литературы, 1958. – 260 с.
Сведения об авторах
Агаев С. Г., д.т.н., профессор, заведующий кафедрой «Технология нефтехимического синтеза», Тюменский государственный нефтегазовый университет, тел.: (3452) 25-69-25 Байда А.А., аспирант кафедры «Технология нефтехимического синтеза», Тюменский государственный нефтегазовый университет, тел.: (3452) 25-69-25 Agaev S. G., Doctor of Technical Sciences, professor, Head of Department «Technology of Petrochemical Synthesis», Tyumen State Oil and Gas University, phone: (3452) 25-69-25 Bayda A.A., postgraduate student, Department «Technology of Petrochemical Synthesis», Tyumen State Oil and Gas University, phone: (3452) 25-69-25
(27) Тема 2005-1-34 Д Моделирование вытеснения нефти полимердисперсными системами Никифоров А. И., Тимошенко И. Е., Газизов А. Ш., Газизов А. А. Формирование барьеров в неоднородных пластах при вытеснении нефти полимердисперсными системами // Известия высших учебных заведений. Нефть и газ. 2005, № 1. С. 34 – 42.
УДК 532.546
ФОРМИРОВАНИЕ БАРЬЕРОВ В НЕОДНОРОДНЫХ ПЛАСТАХ ПРИ ВЫТЕСНЕНИИ НЕФТИ ПОЛИМЕРДИСПЕРСНЫМИ СИСТЕМАМИ
Поздняя стадия разработки месторождений характеризуется наличием обширных промытых высокопроницаемых зон, по которым фильтруются основные массы закачиваемой воды, не оказывая существенного влияния на выработку менее проницаемых участков и пропластков. Разработаны методы увеличения нефтеотдачи пластов, основанные на повышении фильтрационного сопротивления обводненных зон. В частности, широко применяются методы, в которых предусматривается закачка полимердисперсных систем (ПДС) [1-3]. Сущность метода ПДС состоит в последовательной закачке воды, оторочки слабо концентрированного полимерного раствора (обычно полиакриламида) и воды с дисперсными частицами (частицами горных пород). Механизм воздействия ПДС определяется следующими процессами взаимодействия компонентов системы с пластом и между собой [2,3]. Макромолекулы полимера, двигаясь по пласту, адсорбируются на стенки поровых каналов [4,5]. Поступление твердых частиц в эту среду сопровождается осаждением одной их части на стенки каналов из-за взаимодействия со свободными функциональными группами полимера, закрепившегося на поверхности пор. Другая их часть вступает во взаимодействие с макромолекулами полимера в движущейся жидкости, образуя при этом агрегаты в виде одной или нескольких частиц с прикрепленными к ним макромолекулами полимера. В свою очередь агрегаты могут находиться в подвижном состоянии, осаждаться на поверхности пор или механически удерживаться в сужениях поровых каналов, существенно изменяя при этом свойства пористой среды. Образование агрегатов глубоко в пласте на стенках поровых каналов и в свободном пространстве пор приводит к локальному возрастанию фильтрационного сопротивления из-за сужения и частичного или полного блокирования отдельных поровых каналов, что, в свою очередь, приводит к изменению направлений фильтрационных течений и к повышению охвата пласта заводнением. В работе представлена математическая модель задачи заводнения нефтяных пластов с применением ПДС. Замыкающие соотношения получены при помощи идеальной модели пористой среды в виде пучка капилляров различных радиусов. Описаны явления изменения динамической пористости и проницаемости, связанные с изменениями структуры порового пространства под воздействием дисперсной примеси. Поровое пространство характеризуется функцией распределения пор по размерам, а состав примеси - функцией распределения частиц по размерам. Численное решение получено на основе конечно-элементного метода контрольных объемов. Законы сохранения. Разобьем условно пористую среду на две части [7], характеризуемые пористостями m 1 и m 2, которые меняются в процессе насыщения пласта водой: m 1 - часть порового пространства, занятого подвижными жидкостями (динамическая пористость); m 2- часть порового пространства с неподвижными жидкостями; Формально явление в крупномасштабном приближении можно описать следующими законами сохранения массы и импульса. Уравнения сохранения масс фаз и компонентов для первого континуума:
В приведенных выше уравнениях нефти соответствует индекс i= o, воде – i= w; j – номер компонента (j =1 – соответствует полимеру, j =2 – дисперсной примеси); Уравнения движения фаз возьмем в виде обобщенного закона Дарси:
где P – давление; Уравнения движения необходимо записать не только для нефти и воды, но и для примесей, движущихся с фильтрационным потоком. При моделировании заводнения с применением полимера обычно предполагается, что полимер движется со скоростью воды, но скорость воды определяется некоторой фиктивной вязкостью, зависящей от концентрации полимерного раствора: Уравнения сохранения масс фаз и компонентов для второго континуума:
где Насыщенность пласта водой связана с водонасыщенностями и пористостями двух сред соотношением Масса j -го компонента, изъятая из подвижного континуума, будет составлена из масс компонента, адсорбированного на пористый скелет, содержащегося в жидкости, перешедшей в неподвижное состояние, и провзаимодействовавшего с другими компонентами. Особенности описываемого явления будут определяться динамической пористостью m 1, пористостью второй среды m 2, коэффициентами фильтрации Функция распределения пор по размерам. Одной из основных характеристик микронеоднородности пористой среды является функция распределения пор по размерам. Моделированию изменений параметров среды и потока при взаимодействии монодисперсной взвеси с поровой структурой с использованием функции распределения пор по размерам посвящены работы [6,7], где для описания воздействия на пласт ПДС также использована функция распределения пор по размерам. Будем считать, что каждая «точка» пласта характеризуется своей функцией распределения
Индивидуальность процесса определяется коэффициентами ur и u h. Полученное уравнение отличается от уравнения работы [8] наличием слагаемого u h в левой части. Уравнение является достаточно общим и может быть использовано в широком круге задач, в которых учитываются структурные изменения порового пространства в процессе фильтрации жидкостей. Функция распределения частиц по размерам. Если фильтрационный поток переносит различные дисперсные частицы, размеры и количество которых меняется в потоке, то их состав можно характеризовать функцией распределения частиц по размерам Кинетику изменения этой функции опишем аналогично тому, как это сделано для функции распределения пор по размерам. Пусть uv и uζ будут соответственно скоростью роста размера и интенсивностью изменения количества частиц одного типоразмера в потоке. Тогда уравнение сплошности для функции распределения частиц по размерам запишем в виде
Индивидуальность процесса здесь также определяется коэффициентами uv и uζ. Скорости сужения и блокирования поровых каналов. Для оценки скоростей сужения и блокирования поровых каналов смоделируем реальную пористую среду системой цилиндрических капилляров различных радиусов [9,10]. Будем считать, что: 1) в каждом таком капилляре присутствуют нефть и вода в объемах, пропорциональных их насыщенностям; 2) капиллярная разность давлений в фазах равна нулю (т.е. граница раздела между жидкостями плоская, вода вытесняет нефть из капилляра поршневым образом); 3) частицы в жидкости распределены равномерно; 4) отношение радиуса горла к радиусу канала одинаково для всех капилляров и сохраняется в процессе осаждения частиц на стенки каналов; 5) поровый канал блокируется полностью частицей, попавшей в горло, если характерный размер частицы не меньше диаметра горла; 6) собственная пористость массы осевших частиц пренебрежимо мала сравнительно с пористостью пласта. Допущение 4 позволяет характеризовать распределение горла по размерам той же функцией распределения, что и распределение пор по размерам. При двухфазном течении по предположению примеси переносятся только водой, поэтому скорость сужения цилиндрического порового канала, вызванное осаждением частиц на его стенки, примем в виде (диффузионное приближение [11, 12, 13-15]
где Для модельной среды средняя скорость
где z - коэффициент извилистости капилляра [9], которое легко получить, учитывая допущения 1-3 и, комбинируя закон Пуазейля для капилляра и закон Дарси для элемента пористой среды, представленного пучком капилляров. Чтобы оценить скорость блокирования поровых каналов, воспользуемся четвертым допущением, согласно которому радиус горла Тогда скорость
Интенсивности массобмена. Интенсивность перехода воды и нефти из подвижного состояния в неподвижное можно вычислить по доле блокированных поровых каналов:
Интенсивность перехода компонентов в неподвижное состояние
Суммарная интенсивность оседания компонентов на стенки поровых каналов:
Общая интенсивность перехода компонентов в неподвижное состояние составит
Скорости роста и изъятия частиц из процесса и интенсивности массобмена отдельными компонентами активных примесей между континуумами – величины, которые определяются конкретной технологией разработки нефтяных пластов. Скорости роста и изъятия частиц. В процессе взаимодействия полимера с частицами происходит рост и агрегирование частиц и, следовательно, необходимо определиться с величинами uv и uz в уравнении для функции распределения частиц по размерам (7). Пусть индекс j=1 соответствует полимеру, j=2 - частицам и агрегатам. Скорость укрупнения частиц только при их взаимодействии с полимером зависит от концентраций полимера и частиц, от размера последних. Примем эту зависимость в виде
где звездочкой помечены некоторые предельные (критические) концентрация полимера и размер частиц, при достижении которых взаимодействие прекращается. Основанием для введения в скорость укрупнения критических величин послужили экспериментальные факты [2,3]. Замечено, что укрупнение частиц в полимере наблюдается при малых концентрациях и прекращается, если концентрация превысит некоторую критическую величину. Рост частицы не может продолжаться бесконечно ввиду ограниченного количества сорбционных центров на ней и в силу того, что присоединенные макромолекулы полимера препятствуют присоединению последующих макромолекул. При движении полимердисперсной смеси по пласту изменение числа частиц в потоке в каждой точке пласта происходит по трем причинам. Во-первых, частицы поступают с фильтрационным потоком. Во-вторых, частицы осаждаются на поверхности пор. В-третьих, отдельные частицы и агрегаты объединяются между собой. Поэтому интенсивность изменения числа частиц можно представить в виде трех слагаемых: Чтобы определить изменение содержания частиц в каждой точке пласта из-за их конвективного переноса, воспользуемся уравнением неразрывности для частиц одного типоразмера:
и уравнением (2) для ансамбля частиц. После несложных преобразований получим уравнение
которое может быть использовано при вычислении Будем считать, интенсивность осаждения частиц различного размера одинакова, тогда
Процесс объединения агрегатов опишем с использованием теории Смолуховского [18]. Согласно этой теории кинетика коагуляции частиц определяется уравнением
где Будем считать, что интенсивность взаимодействия частиц пропорциональна их размерам, и возьмем ядро коагуляции в виде
где Интенсивность перехода полимера в неподвижное состояние равна
где Интенсивность перехода частиц в неподвижное состояние равна
где интенсивность осаждения агрегатов Пористость и проницаемость. Изменение динамической пористости, вызванное структурными изменениями порового пространства, оценим, представив пористость для текущего момента времени
Изменение абсолютной проницаемости оценим, также представив проницаемость для текущего момента времени
Численная реализация.В качестве метода решения выбрали метод конечных элементов. Область фильтрации W разбивалась на треугольные конечные элементы W l (l=1,L; L - количество элементов) и решение задачи на каждом элементе отыскивалось в виде
где I - множество узлов, принадлежащих l - му элементу; wi – линейные базисные функции; Pi, Функции распределения пор и частиц по размерам также отыскивались при помощи конечно-элементного метода контрольных объемов. Для этого области решения уравнений для функций j и y покрывались сеткой одномерных конечных элементов и использовалось линейное представление искомых функций на каждом элементе. По времени применялась неявная схема. При интегрировании конвективных членов уравнений (6) и (7) учитывались характеристические направления. В целом алгоритм решения задачи таков. По известным характеристикам пластовой системы (по известным k, m 1, S 1 w, C 1 j, S 2 w, C 2 j (j =1,2)) вычисляется давление, насыщенность и концентрации примесей для последующего момента времени из решения задач (1) - (5). Затем по рассчитанным полям вычисляются новые распределения пор и частиц по размерам (решаются задачи Коши для уравнений (6), (7)). Далее вычисляются новые значения полей проницаемости и пористости и осуществляется переход к новому временному шагу. Следует отметить, что задачи Коши, которые решаются на каждый момент времени во всех сеточных узлах, можно осуществлять параллельно, что удобно делать на современных ЭВМ с параллельной архитектурой. Результаты расчетов. В следующем примере параметры пластов приближены к средним показателям реальных пластов нефтяных месторождений Татарстана, а параметры модели подбирались из условия близости эффектов, наблюдаемых в численном эксперименте и в промысловых условиях. Выполнены расчеты для элемента пятиточечной системы заводнения пласта размерами 196м·196м, пористостью 0,2. Дебиты скважин постоянные – 10м3/сут. Задача решалась до достижения обводненности отбираемой продукции 96%. Полимер закачивался в пласт в течение 10 суток с момента достижения обводненности отбираемой продукции 94%. Оторочка частиц закачивалась в течение 7 суток, через 30 суток после прекращения поступления в пласт полимера. Суспензия содержала частицы размером 0 - 10-16 (м3). Максимум в функции распределения частиц по размерам приходился на частицы размером 5,2·10-17(м3). Сетка треугольных конечных элементов состояла из 4802 элементов и имела 2500 узлов. D =2·10-9(м2/с), h =0.2, L =10-4(м), β =3,4, γ =3·10-2(1/м3сут), ξ =5·1017(1/м3сут), ν*=2·10-16 (м3). На рис. 1 показана проницаемость пласта до и после воздействия на пласт ПДС.
Видно, что в результате воздействия блокирована высокопроницаемая промытая часть пласта (рис. 2), насыщенность пласта водой и вовлечение в разработку запасов нефти, остававшиеся не выработанными при обычном заводнении.
Повышение охвата пласта заводнением и вовлечение в разработку дополнительных запасов нефти сопровождается падением обводненности продукции скважин (рис. 3), продлением «жизни» месторождения и повышением коэффициента извлечения нефти.
Заключение Представлена математическая модель и численные результаты воздействия на нефтяные пласты полимердисперсными системами. Замыкающие соотношения получены при помощи идеальной модели пористой среды в виде пучка капилляров различных радиусов. Смоделированы изменения структуры порового пространства в результате воздействия. Для этого использованы функции распределения пор и частиц по размерам. Получены уравнения, описывающие эволюцию функций распределения. Модель позволяет предсказать, в каком месте происходят изменения коллекторских свойств пласта, в какое время и как изменения отразятся на нефтеотдаче в зависимости от конкретных физико-геологических условий и режимов заводнения. Выполнено сравнение функций распределения пор по размерам, полученных в результате экспериментов по влиянию ПДС на поровое пространство на насыпных моделях и в численном расчете. На численном примере продемонстрировано влияние барьеров, формирующихся при применении полимердисперсных систем, на коэффициент извлечения нефти в случае неоднородного пласта. Формирование барьеров приводит к повышению охвата пласта заводнением и вовлечению в разработку дополнительных запасов нефти, сопровождается падением обводненности продукции скважин и продля
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.65.134 (0.013 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

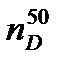 = f (
= f (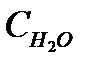 ) можно выделить три области. Первая область – до содержания воды 30 % масс. характеризуется отклонением от прямолинейной зависимости
) можно выделить три области. Первая область – до содержания воды 30 % масс. характеризуется отклонением от прямолинейной зависимости 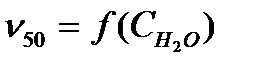 определяется природой спирта и содержанием воды в МЭ. Вязкость МЭ, содержащих ИПС, самая низкая по сравнению с другими МЭ и в наименьшей степени зависит от содержания воды
определяется природой спирта и содержанием воды в МЭ. Вязкость МЭ, содержащих ИПС, самая низкая по сравнению с другими МЭ и в наименьшей степени зависит от содержания воды 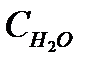 . На зависимостях
. На зависимостях 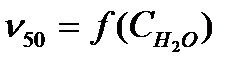 для МЭ, содержащих ЦГС и ТБС, имеется по два максимума при различном содержании воды. При этом вязкости так велики, что их измерение не представляется возможным. На наш взгляд, появление максимумов на зависимостях
для МЭ, содержащих ЦГС и ТБС, имеется по два максимума при различном содержании воды. При этом вязкости так велики, что их измерение не представляется возможным. На наш взгляд, появление максимумов на зависимостях  связано с обращением МЭ. Данные по вязкости только подтверждаются ранее полученными результатами по растворимости, показателю преломления и по температуре застывания.
связано с обращением МЭ. Данные по вязкости только подтверждаются ранее полученными результатами по растворимости, показателю преломления и по температуре застывания.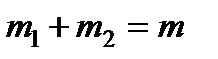 . Будем считать, что фильтрация изотермическая, жидкости несжимаемы, примеси (полимер и дисперсные частицы) переносятся только водой, концентрация их мала.
. Будем считать, что фильтрация изотермическая, жидкости несжимаемы, примеси (полимер и дисперсные частицы) переносятся только водой, концентрация их мала.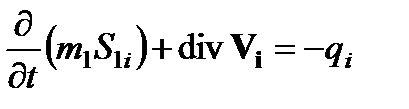 ,
, 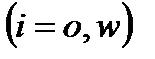 , (1)
, (1)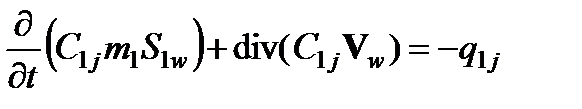 (j = 1,2). (2)
(j = 1,2). (2)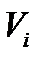 - скорости фильтрации i -й фазы;
- скорости фильтрации i -й фазы; 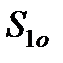 и
и 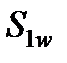 - нефте- и водонасыщенность первой среды:
- нефте- и водонасыщенность первой среды: 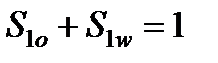 (
(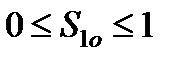 );
);  - объемная концентрация j -го компонента в первом континууме;
- объемная концентрация j -го компонента в первом континууме; 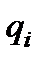 - интенсивность перетока i -й фазы из подвижного континуума в неподвижный;
- интенсивность перетока i -й фазы из подвижного континуума в неподвижный; 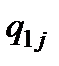 - интенсивность изъятия j - го компонента из подвижного (индекс 1) континуума.
- интенсивность изъятия j - го компонента из подвижного (индекс 1) континуума.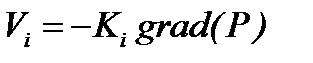
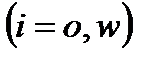 , (3)
, (3)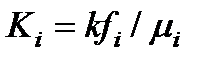 ,
, 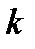 – абсолютная проницаемость пласта;
– абсолютная проницаемость пласта; 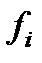 - относительная фазовая проницаемость,
- относительная фазовая проницаемость, 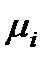 - динамическая вязкость.
- динамическая вязкость.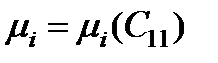 [4]. Наличие твердых частиц малой концентрации в фильтрующейся воде мало сказывается на фильтрационной способности последней. Поэтому можно считать, что собственно частицы движутся со скоростью воды, не изменяя ее вязкости.
[4]. Наличие твердых частиц малой концентрации в фильтрующейся воде мало сказывается на фильтрационной способности последней. Поэтому можно считать, что собственно частицы движутся со скоростью воды, не изменяя ее вязкости. ,
, 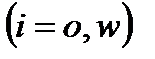 , (4)
, (4)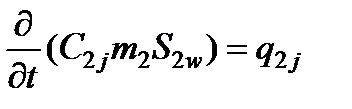 (j = 1,…, n), (5)
(j = 1,…, n), (5)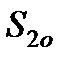 и
и 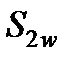 - нефтенасыщенность и водонасыщенность второй среды:
- нефтенасыщенность и водонасыщенность второй среды:  ;
; 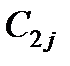 - концентрация j -го компонента во втором континууме;
- концентрация j -го компонента во втором континууме;  - интенсивность перехода j -го компонента в неподвижный континуум.
- интенсивность перехода j -го компонента в неподвижный континуум.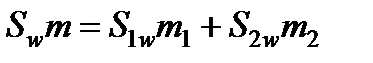 .
.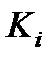 (i= o, w) и массообменными членами qi (i= o, w), q 1 j, q 2 j (j = 1,2). При моделировании конкретной ситуации в пласте систему уравнений необходимо дополнить начальными и граничными условиями.
(i= o, w) и массообменными членами qi (i= o, w), q 1 j, q 2 j (j = 1,2). При моделировании конкретной ситуации в пласте систему уравнений необходимо дополнить начальными и граничными условиями.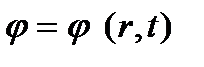 , где
, где 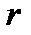 - радиус порового канала. Для начального момента времени распределение поровых каналов по размерам будем считать известным, т.е.
- радиус порового канала. Для начального момента времени распределение поровых каналов по размерам будем считать известным, т.е. 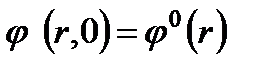 . Эволюция функции распределения пор по размерам описывается уравнением
. Эволюция функции распределения пор по размерам описывается уравнением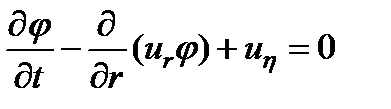 . (6)
. (6)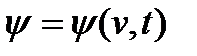 , где v - объем частицы (далее под размером частиц понимается их объем).
, где v - объем частицы (далее под размером частиц понимается их объем).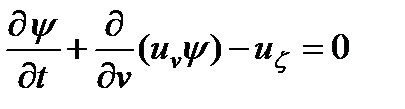 . (7)
. (7)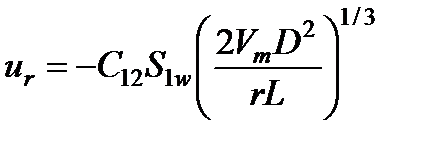 , (8)
, (8)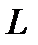 - длина порового канала;
- длина порового канала; 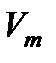 - среднее значение скорости жидкости в канале;
- среднее значение скорости жидкости в канале; 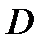 - коэффициент диффузии частиц.
- коэффициент диффузии частиц. в поровом канале радиуса r связана с суммарной скоростью фильтрации
в поровом канале радиуса r связана с суммарной скоростью фильтрации 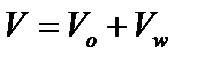 соотношением
соотношением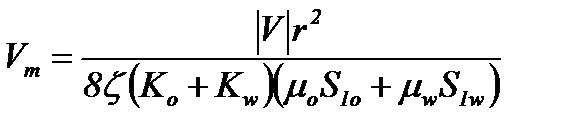 , (9)
, (9)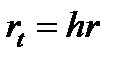 , где
, где 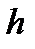 - некоторая константа, одинаковая для всех каналов. Предположим, что доля блокированных капилляров радиуса r пропорциональна количеству частиц, попавших в такие каналы, размеры которых удовлетворяют условию блокирования
- некоторая константа, одинаковая для всех каналов. Предположим, что доля блокированных капилляров радиуса r пропорциональна количеству частиц, попавших в такие каналы, размеры которых удовлетворяют условию блокирования  , где
, где 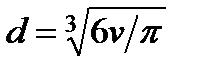 - диаметр частицы объемом v. Коэффициент пропорциональности (совместно с коэффициентом извилистости обозначим его
- диаметр частицы объемом v. Коэффициент пропорциональности (совместно с коэффициентом извилистости обозначим его 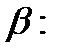
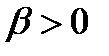 ) можно назвать коэффициентом формы и при помощи него учитывать несовершенство формы частиц и каналов.
) можно назвать коэффициентом формы и при помощи него учитывать несовершенство формы частиц и каналов.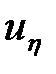 будет равна [15]
будет равна [15]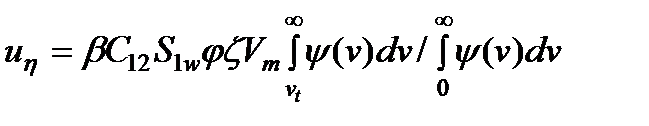 , где
, где 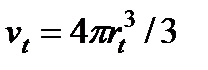 . (10)
. (10)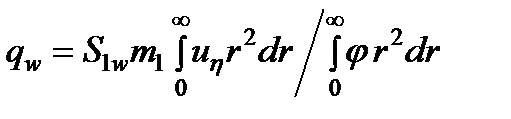 ,
,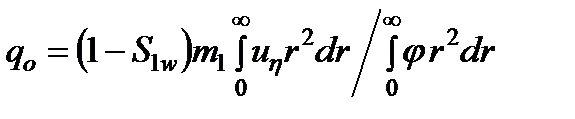 . (11)
. (11)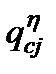 будет
будет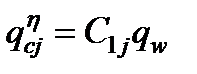 . (12)
. (12)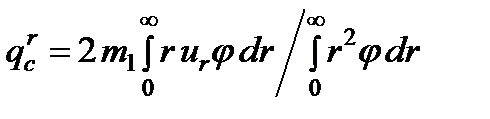 . (13)
. (13)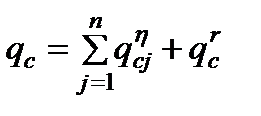 . (14)
. (14)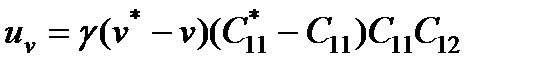 , (15)
, (15)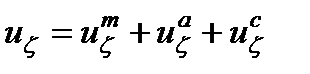 , где первое отвечает за конвективный перенос частиц, второе – за осаждение, третье – за объединение.
, где первое отвечает за конвективный перенос частиц, второе – за осаждение, третье – за объединение.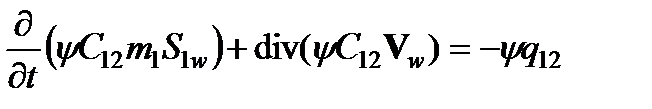 (16)
(16) , (17)
, (17)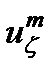 .
.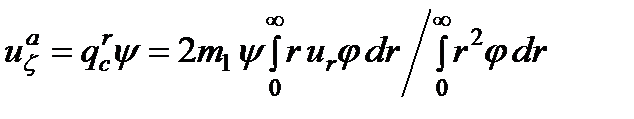 . (18)
. (18)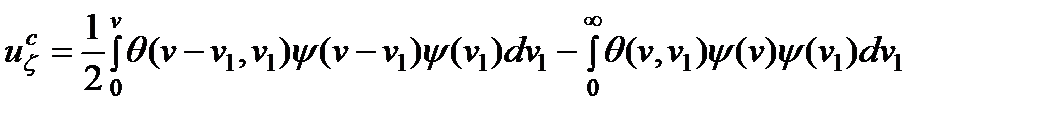 , (19)
, (19)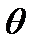 - ядро коагуляции,
- ядро коагуляции, 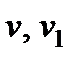 - размер агрегата после коагуляции и размер присоединенного кластера соответственно.
- размер агрегата после коагуляции и размер присоединенного кластера соответственно.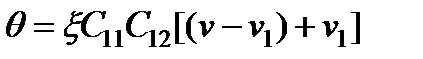 , (20)
, (20)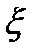 - некоторая константа, которая должна подбираться в зависимости от структуры потока, от свойств переносящей полимер жидкости, в частности, от вязкости и от кислотности среды.
- некоторая константа, которая должна подбираться в зависимости от структуры потока, от свойств переносящей полимер жидкости, в частности, от вязкости и от кислотности среды.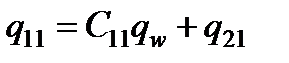 , (21)
, (21)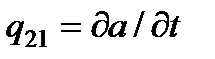 , a - масса адсорбированного полимера, которая определяется изотермой сорбции [4,5].
, a - масса адсорбированного полимера, которая определяется изотермой сорбции [4,5].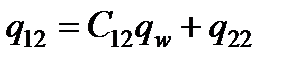 , (22)
, (22)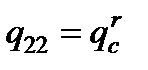 .
. в виде произведения:
в виде произведения: 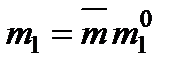 , где фактор изменения пористости
, где фактор изменения пористости 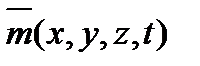 может быть представлен как
может быть представлен как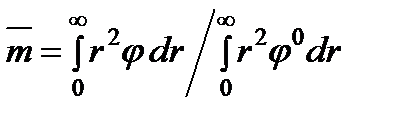 . (23)
. (23)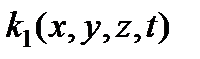 в виде произведения:
в виде произведения: 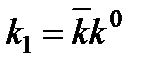 , где фактор остаточного сопротивления
, где фактор остаточного сопротивления 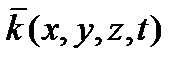 определим, воспользовавшись моделью параллельных капилляров и законом Пуазейля:
определим, воспользовавшись моделью параллельных капилляров и законом Пуазейля: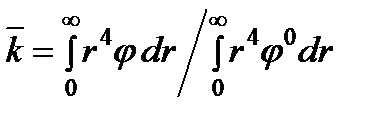 . (24)
. (24)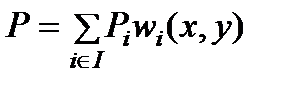 ,
, 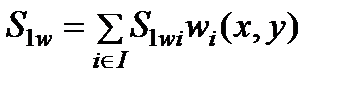 ,
,  ,
,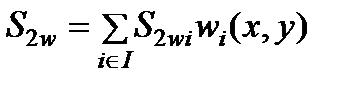 ,
, 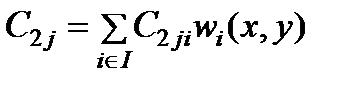 , (25)
, (25)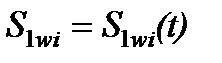 ,
, 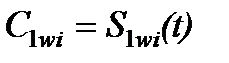 ,
, 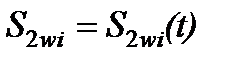 ,
, 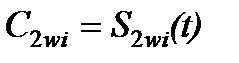 - искомые значения давления, насыщенностей и концентраций в i -м узле. Для их отыскания применялся метод контрольных объемов [19,20,21], где интегралы от членов уравнений, содержащих временную производную, вычислялись с использованием “лампинг”- подхода [19], а конвективные слагаемые интегрировались сучетом направления потока. Для аппроксимации по времени использовалась явная конечно-разностная схема.
- искомые значения давления, насыщенностей и концентраций в i -м узле. Для их отыскания применялся метод контрольных объемов [19,20,21], где интегралы от членов уравнений, содержащих временную производную, вычислялись с использованием “лампинг”- подхода [19], а конвективные слагаемые интегрировались сучетом направления потока. Для аппроксимации по времени использовалась явная конечно-разностная схема.




