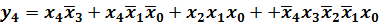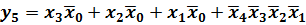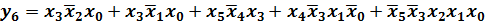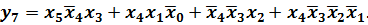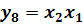Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Табличный метод минимизации логических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
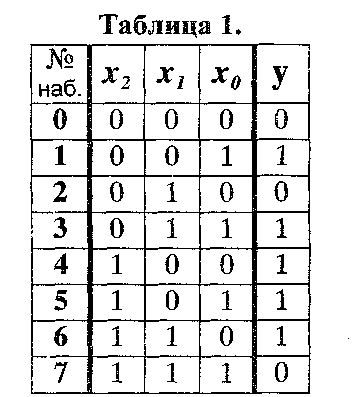
(карты Карно) Карта Карно является специальной формой таблицы истинности, позволяющей не только задать логическую функцию, ко и выполнить и её минимизацию. Рассмотрим логическую функцию, зависящую от 3-х логических переменных, заданную следующей таблицей истинности (таблица 1).
Карта Карно содержит 2 п клеток, расположенных в виде строки (п = 1, 2), либо в виде двумерной матрицы (п > 2). Каждая клетка, как и строка в таблице истинности, соответствует одному набору логических переменных. Для того, чтобы можно было производить минимизацию логической функции, необходимо в смежных в геометрическом смысле клетках карты расположить соседние наборы.
Это можно обеспечить, если наборы переменных, определяющих "координаты" клетки карты Карно, расположить в циклическом коде Грея, у которого каждое следующее значение отличается от предыдущего только в одном разряде. На рис. 1 представлена так называемая эталонная карта Карно для п = 3. Эталонная карта Карно служит для указания расположения переменных, как координат клеток, так и наборов этих переменных. Координатой клеток в горизонтальном направлении служат наборы переменных
Рис. 1. Эталонная карта Карно для п = 3.
Каждая из п переменных встречается в половине наборов без инверсии, а в другой половине с инверсией. Три толстые линии, расположенные с внешней стороны карты Карно, указывают, что в соответствующих им половинах клеток указанная рядом с этой линией переменная встречается в наборе без инверсии и, соответственно, в другой половине с инверсией. Правильность оформления эталонной карты Карно можно проверить следующим образом. Если толстую линию, соответствующую переменной х2 протянуть вправо по горизонтали над клетками карты Карно, то она пройдет над клетками, в которых минимальный номер набора должен совпадать с весом переменной Несмотря на то, что карты Карно изображаются на плоскости, с точки зрения обеспечения соседства их клеток, карты нужно считать трехмерными объектами, так как клетки, расположенные на концах одних и тех же строк и столбцов, также являются соседними. Так карту для трех переменных следует рассматривать как цилиндр со склеенными правым и левым краями. Карту Карно для четырех переменных нужно считать склеенной не только по правому и левому краям, но и по верхнему и нижнему. Таким образом, карта Карно для четырех переменных должна рассматриваться как поверхность тора. Рабочая карта Карно, соответствующая табл.1, будет иметь вид, представленный на рис. 2.
Буква у рядом с косой линией, расположенной в левом верхнем углу карты Карно, обозначает реализуемую логическую функцию, а цифры 0 и 1 в клетках карты указывают значения этой функции на соответствующих наборах. Полученную рабочую карту Карно можно интерпретировать как компактное представление логической функции в СДНФ, либо в СКНФ. Дальнейшее изложение будем вести в предположении, что минимизация ведется в дизъюнктивных формах. Процесс минимизации с помощью карт Карно базируется на использовании операции склеивания и основан на следующих положениях: 1. На картах Карно необходимо выделить монолитные области единичных клеток, образующих строку, столбец, прямоугольник или квадрат и содержащие одну, две, четыре, восемь и т. д. клеток. Эти выделенные области (или контуры покрытия) будут соответствовать импликантам. Очевидно, что одна изолированная клетка будет соответствовать конституенте единицы. Две смежные клетки будут соответствовать импликанте, ранг которой r = п -1, четыре смежные клетки будут соответствовать импликанте, ранг которой г = п -2и т.д. 2. Переменные, от которых импликанта не зависит, входят в соответствующий выделенный контур как в виде 3. На основании закона тавтологии любая единичная клетка может быть включена в любое число различных контуров. 4. Для получения минимальных ДНФ в карте Карно не должно быть лишних покрытий, то есть каждую единичную клетку достаточно использовать хотя бы один раз. 5. Существуют эквивалентные покрытия для получения различных минимальных ДНФ. 6. Существуют функции, для которых СДНФ совпадает с минимальной ДНФ. В этом случае на карте Карно все единичные клетки изолированные. 7. Если в карте Карно нет ни одной 1, то логическая функция эквивалентна константе 0. Если нет ни одного 0, то логическая функция эквивалентна константе 1. Если единицы занимают половину клеток карты Карно и представляют из себя монолитный массив в виде строки, столбца, прямоугольника или квадрата, то соответствующая импликанта состоит из одной переменной со знаком или без знака инверсии. С учетом сказанного на картах Карно рис. 3 можно выделить три контура, содержащих по две единицы.
Рис. 3. Рабочие карты Карно с двумя эквивалентными покрытиями
Два варианта покрытия обусловлены тем, что 1 в клетке с. набором 5 может образовать контур из двух клеток либо с набором 4 (рис. 3а), либо с набором 1 (рис. 3б). Поясним получение импликанты для контура, образованного двумя клетками в нижней строке карты. Переменная
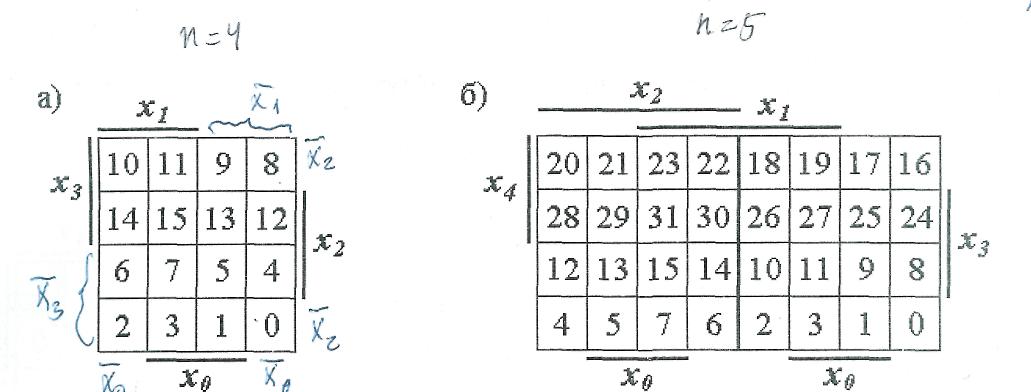
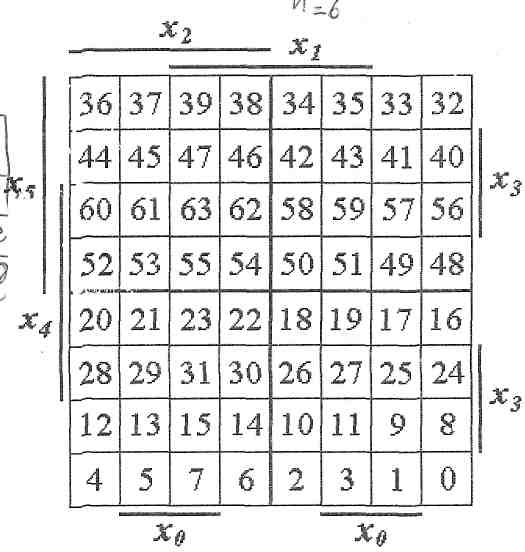
Простота получения этих уравнений показывает существенное преимущество табличного метода карт Карно перед расчетным методом. На рисунке 4 показаны эталонные карты Карно для п = 4, п = 5 и п = 6, причем карты Карно для п =5 и п = 6 можно рассматривать как соответственно две и четыре карты Карно для п= 4, имеющие общие границы (они выделены толстыми центральными линиями). Карты Карно для п = 4, являющиеся составной частью карт Карно для п= 5 и п = 6 и имеющие общие границы, называются соседними. Правило соседства, для какой либо клетки в этих случаях, будет выглядеть так: для любой выделенной клетки соседними являются четыре соседние клетки в карте Карно для п = 4 и клетки, расположенные в соседних картах Карно для п = 4 симметрично выделенной клетке относительно границ соседних карт Карно. Пример. Для клетки с набором 25 на рис. 4,б соседними являются клетки с номерами наборов 9, 27, 17, 24 и 29. Для клетки с набором 2 на рис. 4,б соседними являются клетки 3, 10, 0, 18 и 6. Для клетки с набором 43 на рис. 4,в соседними являются клетки с наборами 59, 42, 35, 41 и 47, 11. Для клетки с набором 22 на рис. 4,в соседними являются клетки с наборами 23, 30, 20, 6 и 54, 18.
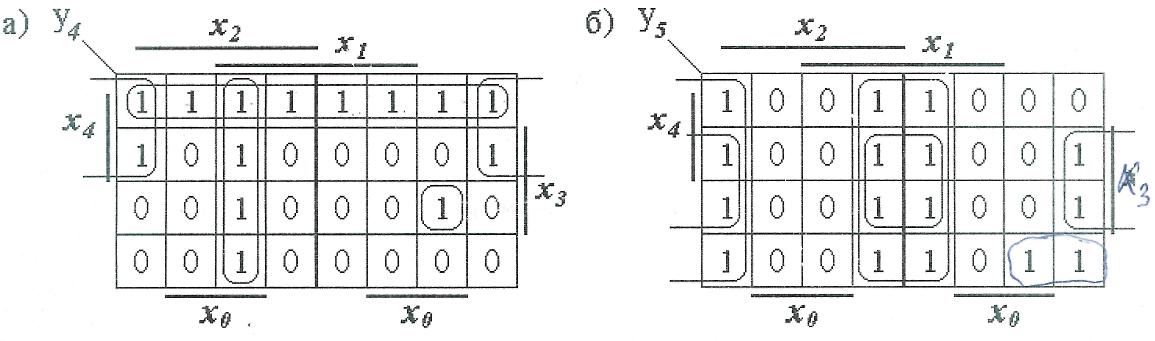
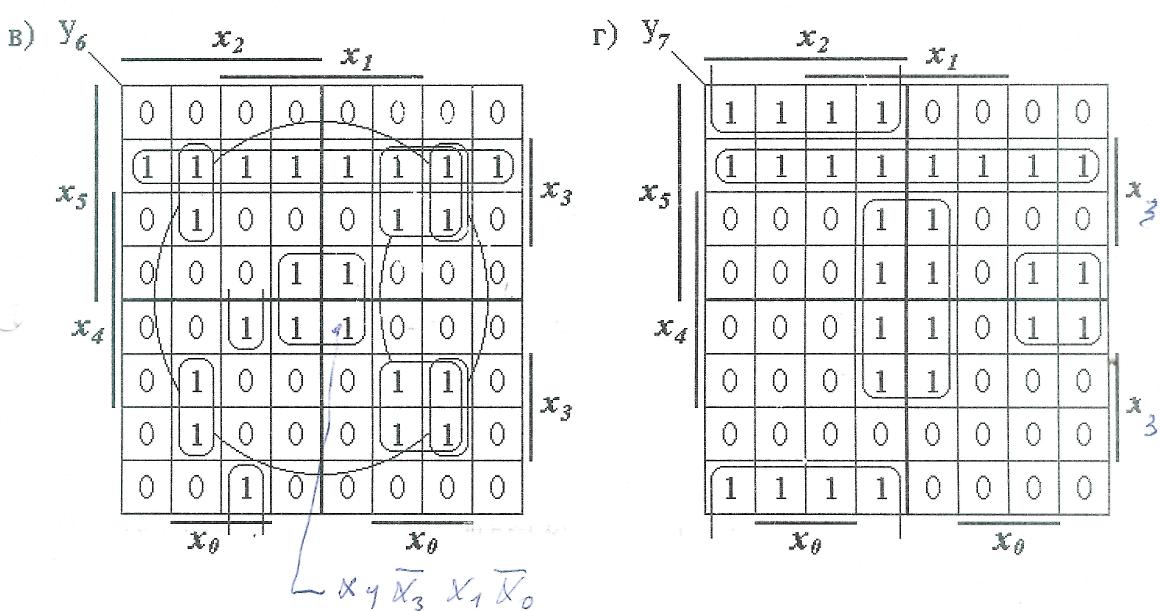
Рис. 4. Эталонные карты Карно для п = 4, п = 5 и п = 6. Рассмотрим еще несколько примеров для функций, зависящих от 4-х, 5-ти и 6-ти переменных. На рис. 5,а четыре 1-е клетки образуют квадрат, которому соответствует импликанта Из карты Карно (рис. 5,б) получаем:
Для карты Карно (рис. 5,в) покажем еще один способ определения импликант, соответствующих выделенным контурам, состоящих в данном случае из двух столбцов. Для левого контура запишем минимальный и максимальный наборы
Рис. 5. Рабочие карты Карно произвольных логических функций,зависящих от четырёх переменных
Если теперь на той же карте Карно выделить контуры, соответствующие импликантам
Для логической функции, представленной на рис. 5,д, можно записать:
Если на той же карте Карно выделить контуры, соответствующие импликантам нуль. Теперь можно сделать следующий вывод: если в карте Карно можно выделить два пересекающихся контура с общей нулевой частью, то импликанты, соответствующие этим контурам, объединяются знаком операции " сумма по mod 2 ". Картам Карно, показанным на рис. 6,а-г, соответствуют следующие выражения: де-Мор-гана, то получим следующее выражение:
Рис 6. Рабочие карты Карно произвольных логических функций, зависящих от пяти и шести переменных
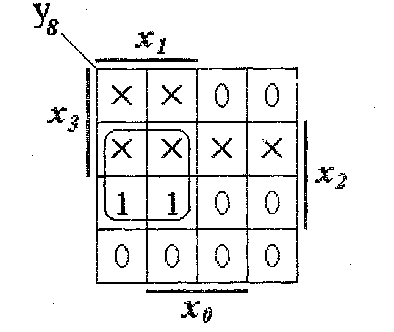
Карты Карно удобно использовать и для минимизации не полностью определенных функций. Безразличные значения логической функции на картах Карно обозначаются каким-либо символом: крестиком, чертой, буквой и т. п. Карта Карно для этого случая приведена на рис. 7.
Рис.7. Рабочая карата Карно для не полностью определенной логической функции. Доопределив безразличные значения у8 на наборах 14 и 15 единицами, получим следующее минимальное выражение:
После реализации этой функции она становится полностью определенной, то есть на безразличных наборах, включенных в контур, будут реализовываться значения 1, а на не включенных в контур - значение 0. Сформулируем в заключение достоинства и недостатки метода минимизации логических функций с помощью карт Карно. Достоинства: 1. Основным достоинством применения карт Карно является компактность, простота и наглядность представления полностью и не полностью определенных логических функций. 2. Их применение оправдано для п = 2, п = 4, п = 5 и п =6, а при определенных навыках даже для п =7 и п =8, что соответствует большинству реально встречающихся задач. 3. Карты Карно можно использовать для минимизации ФАЛ, заданных как в СДНФ, так и в СКНФ. 4. Удобно минимизировать системы булевых функций, так как на картах Карно легко выделять общие части реализуемой системы логических функций. 5. Легко находятся минимальные комбинации контуров по их виду на карте Карно. 6. Карты Карно сразу позволяют реализовать первые два этапа минимизации (склеивание и выявление лишних импликант). Недостатки: 1. Затруднительно использовать карты Карно при п > 6. 2. Метод не является алгоритмическим, многое зависит от навыков разработчика. Удобство обращения и экономия времени во многом зависит от его способности распознавать оптимальные конфигурации покрытия карт Карно.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.247 (0.008 с.) |

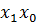 а координатой клеток в вертикальном направлении служит одна переменная х2.
а координатой клеток в вертикальном направлении служит одна переменная х2.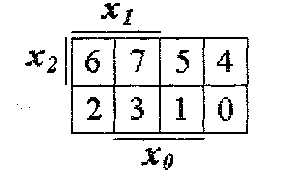
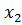 , равным 22 = 4. Аналогично толстая линия, соответствующая переменной
, равным 22 = 4. Аналогично толстая линия, соответствующая переменной 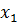 , при перемещении вниз по вертикали пройдет над клетками, в которых минимальный номер набора должен совпадать с весом переменной
, при перемещении вниз по вертикали пройдет над клетками, в которых минимальный номер набора должен совпадать с весом переменной 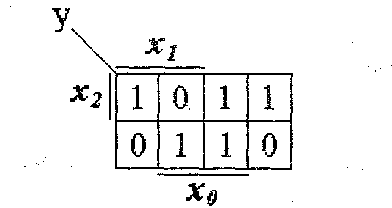
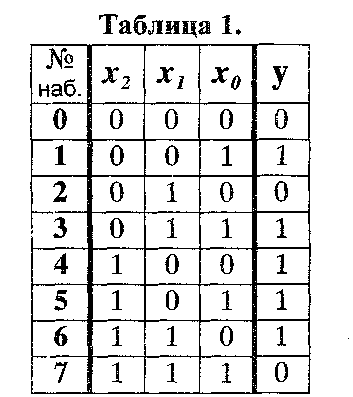 Рис. 2. Рабочая карта Карно для логической функции, заданной таблицей 1.
Рис. 2. Рабочая карта Карно для логической функции, заданной таблицей 1.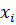 , так и в виде
, так и в виде 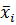 , а остальные переменные только либо в виде
, а остальные переменные только либо в виде 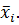
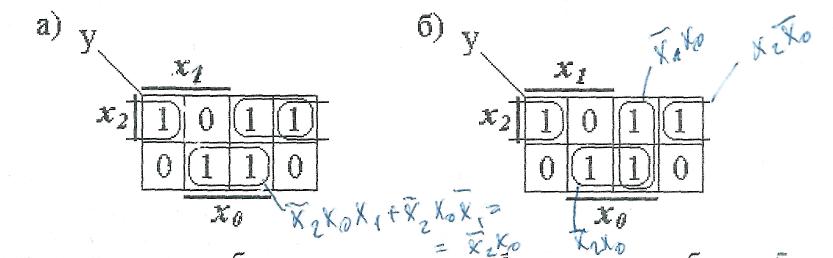
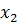 входит в этот контур только с инверсией, переменная
входит в этот контур только с инверсией, переменная 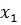 входит в этот контур и с инверсией и без инверсии, поэтому по ней осуществляется склеивание, и она исчезает, переменная
входит в этот контур и с инверсией и без инверсии, поэтому по ней осуществляется склеивание, и она исчезает, переменная 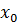 входит в этот контур только без инверсии, поэтому импликанта имеет вид
входит в этот контур только без инверсии, поэтому импликанта имеет вид 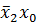 . Для выявленных двух покрытий можно записать:
. Для выявленных двух покрытий можно записать: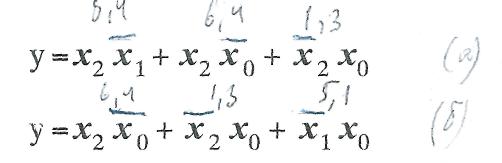
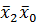 . На рис. 5,б контур, выделенный штриховой линией, оказывается лишним, так как все его клетки являются составными частями четырех контуров из двух клеток.
. На рис. 5,б контур, выделенный штриховой линией, оказывается лишним, так как все его клетки являются составными частями четырех контуров из двух клеток.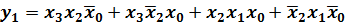 .
.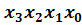 . Таковыми являются наборы 2 и 14. Запишем их двоичные представления 0010 и 1110 одно на другом 1110. Переменные, соответствующие позициям с наложенными 0 и 1, склеиваются, а совпадающие позиции соответствуют искомой импликанте
. Таковыми являются наборы 2 и 14. Запишем их двоичные представления 0010 и 1110 одно на другом 1110. Переменные, соответствующие позициям с наложенными 0 и 1, склеиваются, а совпадающие позиции соответствуют искомой импликанте 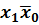 . Аналогичная процедура для правого контура дает импликанту
. Аналогичная процедура для правого контура дает импликанту  . В итоге получаем:
. В итоге получаем: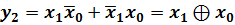
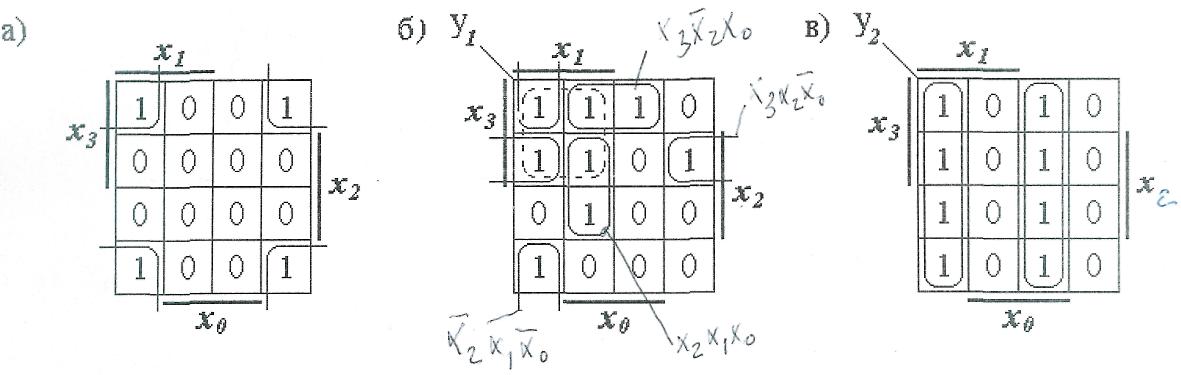
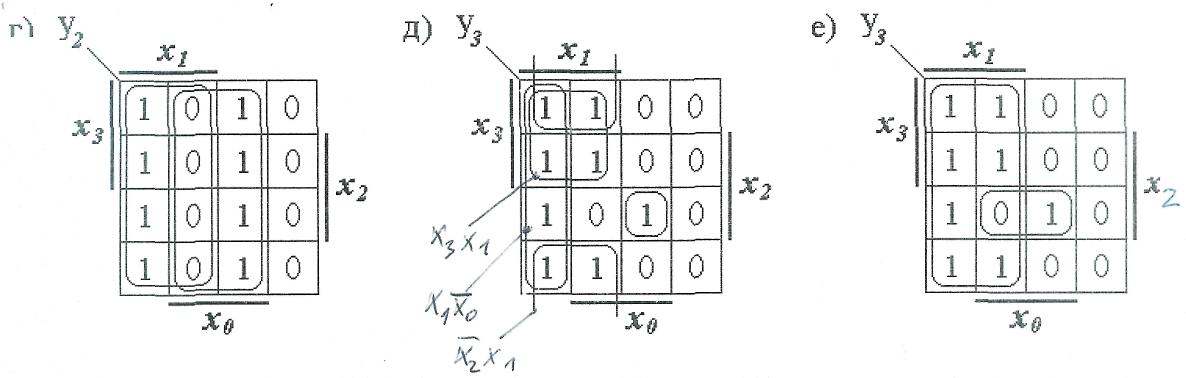
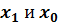 (см. рис. 5,г), то окажется, что общая часть этих контуров будет содержать нулевые клетки.
(см. рис. 5,г), то окажется, что общая часть этих контуров будет содержать нулевые клетки.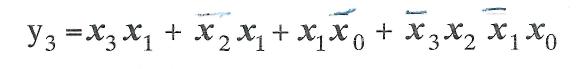
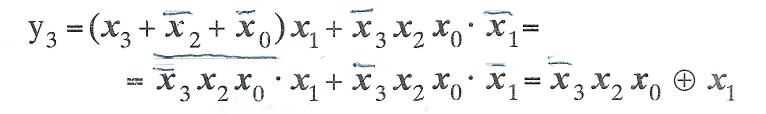
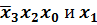 (см. рис. 5,е), то окажется, что общая часть этих контуров содержит
(см. рис. 5,е), то окажется, что общая часть этих контуров содержит