
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наборы логических переменных и их свойстваСодержание книги
Поиск на нашем сайте
Совокупность конкретных значений логических переменных, от которых зависит булева функция, называется набором логических переменных.
Пусть, например, булева функция зависит, от трех переменных х2 , х1и х0. Если, х2 = 0, х1= 1, х0 = 1, то совокупность 011 является одним из возможных наборов для некоторой логической функции f(х2 , х1, х0 ). Наборы могут быть представлены различными способами. Указанный выше набор 011 можно представить как
Представление набора в виде последовательности логических нулей и единиц, можно рассматривать как двоичное число с соответствующим десятичным эквивалентом, например, 0112=310. При этом десятичный эквивалент набора является его номером в таблице истинности. Представление набора в виде двоичного числа позволяет присваивать логическим переменным условные "веса": в наборе х2 х1х0 для x0 вес будет равен 1, логическая переменная х1будет иметь вес, равный 2, а вес переменной х2 - соответственно, равен 4. Именно поэтому логические переменные удобно обозначать индексированными буквами, начиная с индекса 0 для младшей переменной, 1 для следующей переменной и т.д. до индекса п -1, если функция зависит от п переменных. При таком обозначении индекс переменной совпадает с показателем степени основания двоичной системы счисления, т.е. характеризует вес переменной. Так для переменной х5 вес будет равен 25 = 32. Если функция алгебры логики зависит от п переменных, то всего для них существует 2 п наборов, так как добавление одной переменной увеличивает число наборов в два раза. Одна переменная имеет два набора: 0 и 1, две переменные - четыре: 0 = 00, 1=01,2=10, 3 = 11 и т.д. Десятичный эквивалент набора логических переменных называется номером набора.
Наборы можно рассматривать как двоичные векторы Xi, где i- номер набора, однако надо помнить, что они не являются векторами в классическом смысле, так как над ними нельзя выполнять векторные операции. Наборы можно представить в виде вершин n-мерного куба. Это представление здесь рассматриваться не будет. Число переменных, имеющих в наборе значение 1, называется весом набора (не путать с двоичным весом переменных). Вес набора удобно изображать римскими цифрами, так для п = 3 имеем: набор 000 с весом 0; наборы 001, 010, 100 с весом I; наборы 011, 101, 110с весом II и набор 111 с весом III. Двум любым наборам ставится в соответствие целое число, которое называется расстоянием по Хэммингу. Это число совпадает с числом переменных, входящих в наборы различным образом. Расстояние обозначается d(Xi;Xj). Так для п = 4 имеем d(X1;Х13) Расстояние по Хэммингу удовлетворяет следующим условиям: d(Xi;Xj) d(Xi;Xj) = d(Xj;Xi), d(Xi;Xj)+(Xj;Xk) > d(Xi;Xk). Если наборы рассматривать как их десятичные эквиваленты, то для любых двух наборов можно ввести естественную или лексикографическую упорядоченность или отношение порядка (<). Аксиомы отношения порядка. Наиболее простым примером использования отношения полного линейного порядка является естественное расположение наборов переменных в таблицах истинности функций алгебры логики. Не все пары наборов находятся в отношении предшествования, например, 010 и 101, наборы одного веса и др. Поэтому наборы в отношении предшествования являются лишь частично упорядоченными. Те, для которых отношение предшествования не выполняется, называются несравнимыми. Отношение предшествования используется для определения класса монотонных булевых функций.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.240.101 (0.008 с.) |

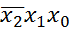 , где знак инверсии говорит о том, что х2 = 0, а отсутствие знака инверсии означает, что х1= 1, х0 = 1.
, где знак инверсии говорит о том, что х2 = 0, а отсутствие знака инверсии означает, что х1= 1, х0 = 1.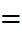 d(0001;1101) = 2, так как только переменные х3и х2 входят в наборы различным образом. Если d(Xi;Xj) = 1, тонаборы называются соседними. Вес набора равен расстоянию по Хэммингу отнулевого набора.
d(0001;1101) = 2, так как только переменные х3и х2 входят в наборы различным образом. Если d(Xi;Xj) = 1, тонаборы называются соседними. Вес набора равен расстоянию по Хэммингу отнулевого набора.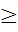 0; d(Xi;Xj) = 0 тогда и только тогда, когда Xi = Xj.
0; d(Xi;Xj) = 0 тогда и только тогда, когда Xi = Xj.


