
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные логические функцииСодержание книги
Поиск на нашем сайте
Задание булевых функций посредством элементарных. Если в логическую функцию вместо переменных подставить некоторые булевы функции, то в результате получается новая булева функция, которая называется суперпозицией подставляемых функций, или, иными словами - сложной функцией. С помощью суперпозиции можно получать более сложные функции, которые могут зависеть от любого числа логических переменных. Запись булевых функций через элементарные булевы функции будем называть формулой реализующей данную логическую функцию.
Пример 1.3.1. Пусть задана элементарная булева функция x˅y. Подставим вместо x функцию x1↓x2. Получаем функцию трех переменных (x1↓x2)˅y. Если вместо переменной y подставить, например, x3⊕x4, то получаем новую функцию от четырех переменных: (x1↓x2)˅(x3⊕x4). Очевидно, что таким образом мы будем получать булевы функции, которые будут выражаться через элементарные булевы функции. Забегая вперед, отметим, что любая булева функция может быть представлена как суперпозиция элементарных функций. Для более компактной записи сложных функций введем следующие соглашения: 1) внешние скобки опускаются; 2) сначала производятся операции в скобках; 3) считается, что приоритет связок убывает в следующем порядке: (инверсия), ˄ или
Пример 1.3.2. В формуле x˄y˅z скобки расставляются следующим образом: ((x˄y)˅z), т.к. согласно нашему соглашению операция ˄ имеет более высокий приоритет, чем операция ˅. В формуле x˅y~z→x скобки расставляются следующим образом: ((x˅y)~(z→x)) В формуле (x⊕y)~z→x˄y˅z скобки расставляются следующим образом: ((x⊕y)~(z→((x˄y)˅(z)))). Формула x→y→z, следуя нашему соглашению, записана не корректно, т.к. расстановка скобок приводит к двум разным функциям: ((x→y)→z) и (x→(y→z)).
Элементарные логические функции
Булеву алгебру, как математическую структуру, представляют следующими объектами: 0, 1, Здесь 0 – символ, обозначающий ложь, 1 - символ, обозначающий истину,
И – как минимум двухместная (то есть зависящая от двух переменных) логическая функция, определяемая как логическое произведение (конъюнкция). Таблица истинности логической функции И имеет вид
Это означает, что это высказывание истинно только в том случае, когда истинны высказывания, от которых оно зависит, в остальных случаях оно ложно. Другие названия: логическое умножение (произведение); логическое «и». Обозначения:
ИЛИ - как минимум двухместная (то есть зависящая от двух переменных) логическая функция, определяемая как логическое сложение (дизъюнкция). Таблица истинности логической функции ИЛИ имеет вид
Это означает, что это высказывание ложно только в том случае, когда ложны все высказывания, от которых оно зависит, в остальных случаях оно истинно. Обозначения:
НЕ – одноместная логическая функция, определяемая как логическое отрицание (инверсия). Таблица истинности логической функции НЕ имеет вид
Обозначения:
= - отношение эквивалентности. Читается как "равно".
Рассмотренные логические функции И, ИЛИ, НЕ являются элементарными булевыми функциями. В более общем случае булеву функцию от n переменных можно задать таблицей истинности, в которой наборы значений аргументов расположены в порядке возрастания их номеров: сначала идет набор, представляющий собой двоичное представление нуля (этот набор имеет номер 0); затем идет набор, являющийся двоичным представлением единицы, потом двойки, тройки и т.д. Последний набор состоит из n единиц и является двоичным представлением числа 2 n -1 (такой порядок расположения наборов назовем лексикографическим порядком). Учитывая, что отсчет начинается с 0, а значение булевой функции может быть либо 0 либо 1, заключаем, что существует всего
Пример 1.1.1. (голосование). Рассмотрим устройство, фиксирующее принятие некоторого решения тремя собравшимися. Каждый при одобрении решения нажимает свою кнопку. Если большинство членов голосуют «за», то решение принимается. Это фиксируется регистрирующим прибором. Таким образом, устройство реализует функцию f (x,y,z), таблица истинности которой имеет вид
Булева функция также однозначно задается перечислением всех наборов, на которых она принимает значение 0, либо перечислением всех наборов, на которых она принимает значение 1.Полученную в примере функцию f можно также задать следующей системой равенств: f (0,0,0) = f (0,0,1) = f (0,1,0) = f (1,0,0) =0.
Вектором значений булевой функции y=f(x1,x2,…,xn) называется упорядоченный набор всех значений функции f, при котором значения упорядочены по лексикографическому порядку. Например, пусть функция трех переменных f задана вектором значений (0000 0010) и необходимо найти набор, на котором f принимает значение 1. Т.к. 1 стоит на 7 месте, а нумерация в лексикографическом порядке начинается с 0, то необходимо найти двоичное разложение 6. Таким образом, функция f принимает значение 1 на наборе (110).
Наряду с рассмотренными выше элементарными функциями рассмотрим несколько логических функций, которые находят широкое практическое применение. 1. Импликацией называется булева функция двух переменных, которая определяется следующей таблицей истинности
Читается так: импликация Другое название: логическое включение Обозначения:
2. Эквивалентностью (равнозначность) называется булева функция двух переменных, которая определяется следующей таблицей истинности
Обозначения: Читатается так: «икс один равнозначна икс два».
3. Суммой по модулю 2 называется булева функция двух переменных, которая определяется следующей таблицей истинности
Обозначения:
4. Штрих Шеффера (операция И-НЕ) - этобулева функция двух переменных, которая определяется следующей таблицей истинности
Обозначение: x|y. Запись x|y может читаться так: « не икс или не игрек», «икс и игрек несовместны», «икс штрих Шеффера игрек». 5. Стрелка Пирса (операция ИЛИ-НЕ) - этобулева функция двух переменных, которая определяется следующей таблицей истинности
Обозначение: x↓y. Запись x↓y может читаться так: «ни икс и ни игрек», «икс стрелка Пирса игрек».
Замечание. Символы (инверсия), ˄ или
Задание булевых функций посредством элементарных. Если в логическую функцию вместо переменных подставить некоторые булевы функции, то в результате получается новая булева функция, которая называется суперпозицией подставляемых функций, или, иными словами - сложной функцией. С помощью суперпозиции можно получать более сложные функции, которые могут зависеть от любого числа логических переменных. Запись булевых функций через элементарные булевы функции будем называть формулой реализующей данную логическую функцию.
Пример 1.3.1. Пусть задана элементарная булева функция x˅y. Подставим вместо x функцию x1↓x2. Получаем функцию трех переменных (x1↓x2)˅y. Если вместо переменной y подставить, например, x3⊕x4, то получаем новую функцию от четырех переменных: (x1↓x2)˅(x3⊕x4). Очевидно, что таким образом мы будем получать булевы функции, которые будут выражаться через элементарные булевы функции. Забегая вперед, отметим, что любая булева функция может быть представлена как суперпозиция элементарных функций. Для более компактной записи сложных функций введем следующие соглашения: 1) внешние скобки опускаются; 2) сначала производятся операции в скобках; 3) считается, что приоритет связок убывает в следующем порядке: (инверсия), ˄ или
Пример 1.3.2. В формуле x˄y˅z скобки расставляются следующим образом: ((x˄y)˅z), т.к. согласно нашему соглашению операция ˄ имеет более высокий приоритет, чем операция ˅. В формуле x˅y~z→x скобки расставляются следующим образом: ((x˅y)~(z→x)) В формуле (x⊕y)~z→x˄y˅z скобки расставляются следующим образом: ((x⊕y)~(z→((x˄y)˅(z)))). Формула x→y→z, следуя нашему соглашению, записана не корректно, т.к. расстановка скобок приводит к двум разным функциям: ((x→y)→z) и (x→(y→z)).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.107 (0.009 с.) |

 , ˅ или +, →, ~. Для равносильных связок и оставшихся связок ⊕, |, ↓, следует пока расставлять скобки.
, ˅ или +, →, ~. Для равносильных связок и оставшихся связок ⊕, |, ↓, следует пока расставлять скобки.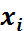 , И, ИЛИ, НЕ, =.
, И, ИЛИ, НЕ, =.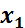
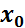
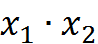 , или
, или 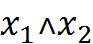 , или
, или 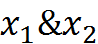 . Читается как " икс один и икс два".
. Читается как " икс один и икс два".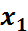
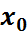
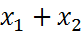 , или
, или 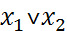 . Читается как " икс один или икс два".
. Читается как " икс один или икс два".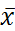 или x. читается как "не икс" или "инверсия икс".
или x. читается как "не икс" или "инверсия икс".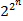 различных булевых функций от n переменных. Таким образом, имеется, например, 16 булевых функций от двух переменных, 256 — от трех и т. д.
различных булевых функций от n переменных. Таким образом, имеется, например, 16 булевых функций от двух переменных, 256 — от трех и т. д.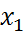
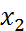
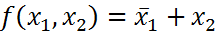
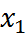
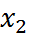
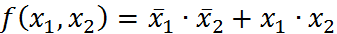
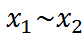 ,
,  , x≡y.
, x≡y.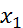
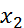
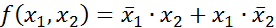

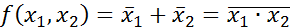
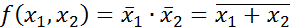
 , ˅ или +, →, ~, ⊕, |, ↓ участвующие в обозначениях элементарных функций будем называть связками или операциями.
, ˅ или +, →, ~, ⊕, |, ↓ участвующие в обозначениях элементарных функций будем называть связками или операциями.


