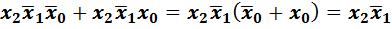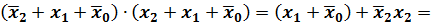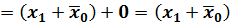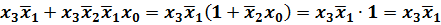Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятия элементарного логического произведения и элементарной логической суммы. Минимизация логических функций.Содержание книги
Поиск на нашем сайте
Логическое произведение любого числа переменных из конечного набора п переменных называется элементарным, когда сомножителями в нем являются либо переменные, либо их отрицания. Например, Количество сомножителей в элементарном произведении называется его рангом. Ранг будем обозначать буквой r. Так для
Логическое произведение, являющееся функцией всех п переменных, от которых зависит логическая функция, называется конституентой единицы (составляющей единицы). Смысл этого термина будет пояснен позже. Для п переменных существует 2 п конституент единицы. Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же переменных и отличаются только знаком инверсии лишь у одной переменной. Например, Логическая сумма любого числа переменных из конечного набора п переменных называется элементарной, когда слагаемыми в ней являются либо переменные либо их отрицания. Например, сумма Количество слагаемых в элементарной сумме называется ее рангом r. Так для
Логическая сумма, являющаяся функцией всех п переменных, от которых зависит логическая функция, называется конституентой нуля (составляющей нуля). Смысл этого термина будет пояснен позже. Для п переменных существует 2 п конституент нуля. Две элементарные суммы одинакового ранга r называются соседними, если они являются функциями одних и тех же переменных и отличаются только знаком инверсии лишь у одной переменной. Например, суммы Сформулируем теперь важнейшие следствия из основных законов булевой алгебры, представив их в виде правил.
Правила склеивания Правило склеивания для элементарных произведений следует из распределительного закона первого рода, закона дополнительности и закона универсального множества: логическую сумму двух соседних произведений некоторого одинакового ранга r можно заменить одним элементарным произведением ранга r - 1, являющимся общей частью исходных слагаемых. Пример. Правило склеивания для элементарных сумм следует из распределительного закона второго рода, закона дополнительности и закона нулевого множества: логическое произведение двух соседних сумм некоторого одинакового ранга r можно заменить одной элементарной суммой ранга r - 1, являющейся общей частью исходных сомножителей. Пример.
Правила поглощения. Правило поглощения для суммы двух элементарных произведений следует из распределительного закона первого рода и законов универсального множества:
логическую сумму двух элементарных произведений разных рангов, из которых одно является составной частью другого, можно заменить произведением, имеющим меньший ранг. Пример: Правило поглощения для произведения элементарных сумм следует из распределительного закона второго рода и законов нулевого множества:
|
||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

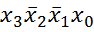 является элементарным, а
является элементарным, а 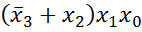 не являются элементарными.
не являются элементарными.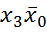 r = 2.
r = 2.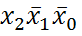 и
и 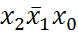 являются соседними, а
являются соседними, а 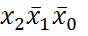 и
и 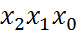 - нет.
- нет.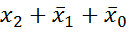 является элементарной, а сумма
является элементарной, а сумма 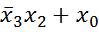 элементарной суммой не является.
элементарной суммой не является.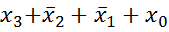 r = 4.
r = 4.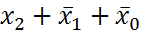 и
и 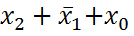 являются соседними, а
являются соседними, а 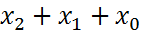 - нет.
- нет.