
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическое произведение двух элементарных сумм разных рангов, из которых одна является составной частью другой, можно заменить элементарной суммой, имеющей меньший ранг.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример.
Привила развертывания Эти правила определяют действия обратные склеиванию. 1. Правило развертывания элементарного произведения в логическую сумму элементарных произведений большего ранга (в пределе до r = п, т.е. до конституент единицы, как и будет рассмотрено ниже) следует из законов универсального множества, распределительного закона первого рода производится в три этапа: - в развертываемое элементарное произведение ранга r вводится в качестве сомножителей n- r единиц, где п - ранг конституенты единицы; - каждая единица заменяется логической суммой некоторой, не имеющейся в исходном элементарном произведении переменной и ее отрицания: - производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходного элементарного произведения ранга г в логическую сумму 2n- r конституент единицы. Пример: развернуть элементарное произведение конституент единицы, зависящих от 4-х переменных. (Последнее следует из того, что максимальный индекс у переменной равен 3). Решение: отсутствуют переменные Пусть п = 3.
Смысл термина "конституента единицы" можно пояснить следующим примером. Пусть п = 3. 1=1
Правило развертывания элементарного произведения используется для минимизации логических функций. Пример. Пусть требуется минимизировать логическую функцию вида
Видно, что все элементарные произведения имеют одинаковый ранг r = 2, следовательно, правило поглощения нельзя применить; кроме того ни одна пара произведений не является соседней, так как произведения имеют различные переменные, т.е. нельзя применить и правило склеивания. Если же развернуть произведение
то есть произведение 1. Правило развертывания элементарной суммы ранга r до произведения элементарных сумм ранга п (конституент нуля) следует их законов нулевого множества и распределительного закона второго рода и производится в три этапа: - в развертываемую сумму ранга r в качестве слагаемых вводится n - r нулей; - каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной сумме переменной и ее отрицания:
-получившееся выражение преобразуется на основе распределительного закона второго рода так, чтобы исходная сумма ранга r развернулась в логическое произведение 2 n - r конституент нуля. Пример: развернуть элементарную сумму конституент нуля, зависящих от 4-х переменных. Последнее следует из того, что максимальный индекс равен 3. Решение: отсутствуют переменные Пусть п = 2.
Смысл термина "конституента нуля" можно пояснить следующим примером. Пусть п = 2. 0=0+0=
Правило развертывания элементарной суммы также используется для минимизации ФАЛ. Пример: пусть Операции склеивания и поглощения здесь применить нельзя. Однако, если развернуть сумму
т.е. сумма Правила склеивания, поглощения и развертывания лежат в основе построения различных методов минимизации логических функций.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.106.170 (0.008 с.) |

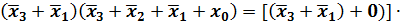
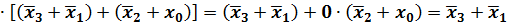
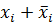 = 1;
= 1;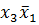 в логическую сумму
в логическую сумму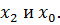
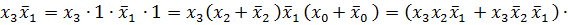
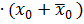 =
= 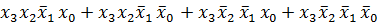
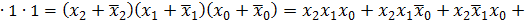
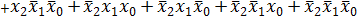
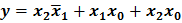
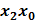 до конституент единицы (в данном случае п = 3), то выражение упростится:
до конституент единицы (в данном случае п = 3), то выражение упростится: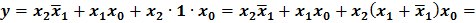
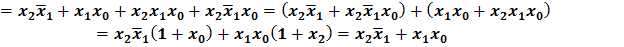
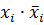 = 0;
= 0;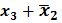 в логическое произведение
в логическое произведение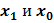 .
.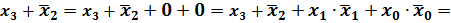
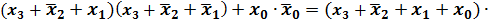
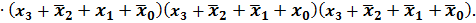
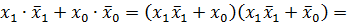
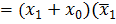 +
+ 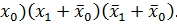
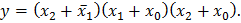 Требуется минимизировать данную функцию.
Требуется минимизировать данную функцию.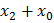 до конституент нуля (в данном случае п = 3), то выражение упростится:
до конституент нуля (в данном случае п = 3), то выражение упростится: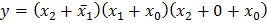 =
= 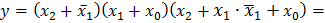
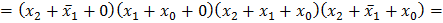
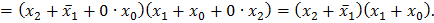
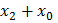 оказалась лишней.
оказалась лишней.


