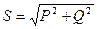Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование разветвленной цепи переменного токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
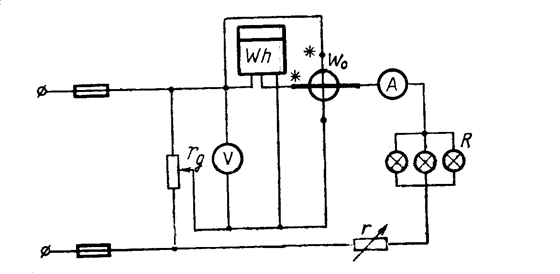
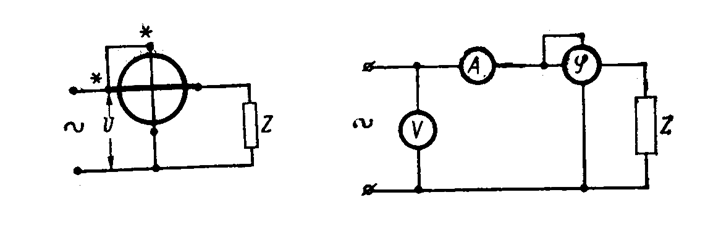
Цель работы. Научиться измерять ток, напряжение и мощность в цепях переменного тока. Практически изучить явления в параллельной цепи, содержащей индуктивность и емкость. План работы. 1. Ознакомиться с работой и оборудованием на рабочем месте, записать или измерить величину активного сопротивления катушки. 2. Собрать цепь (рис. 11) и после проверки руководителем подключить ее к источнику тока. 3. Измерить ток, напряжение и мощность при разомкнутом и замкнутом рубильнике Р. 4. Выполнить необходимые вычисления, сравнить результаты и сделать выводы. 5. Меняя величину индуктивности или емкости, добиться резонанса токов. 6. Измерить токи и напряжения в режиме резонанса токов. 7. Сравнить результаты измерений и сделать выводы. Пояснения к работе. При выполнении этой работы проделать три цикла измерений: 1) при отключенной емкости С; 2) при подключенной емкости; 3) в режиме резонанса токов.
Рис. 11. К практической работе 7
. При разомкнутом рубильнике Р цепь содержит индуктивное и активное сопротивления (на рисунке 11 активное сопротивление катушки изображено вынесенным из нее). Измерив, напряжение на зажимах цепи, ток в ней и ее активную мощность, подсчитать полную мощность цепи S, ее полное сопротивление z, соs φ, активную и реактивную составляющие тока, используя соотношения из треугольников сопротивлений, тока и мощностей. Результаты измерений и вычислений записать в таблицу.
В этой таблице Iс — ток в емкостной ветви; IL — ток в индуктивной ветви. При замкнутом рубильнике Р получается параллельная цепь с индуктивностью и емкостью. В этой цепи, кроме величин, измеряемых в предыдущем случае, определить токи в емкостной и индуктивной ветвях. Результаты измерений и вычислений записать в ту же таблицу. Чтобы получить в цепи резонанс, изменяя величину емкости или индуктивности, добиться минимального показания амперметра, включенного до разветвления, так как при резонансе токов общий ток цепи состоит только из активной составляющей. Показания всех приборов, отмеченные при резонансе, записать в ту же таблицу. Сравнить между собой токи в неразветвленном участке цепи I до подключения и после подключения емкости. Чем объяснить, что после подключения емкости ток в неразветвленном участке цепи уменьшился, а ток индуктивной ветви IL остался прежним? Подсчитать разность между реактивными токами цепи в первом и во втором опыте и сравнить ее с током емкостной ветви Iс. Чем объяснить, что они приблизительно равны? Почему после подключения емкости показания ваттметра не изменились? Дополнительный материал к работе. Резонанс токов. Сущность явления и векторные диаграммы. Если параллельно индуктивному токоприемнику (он может представлять собой эквивалент ряда индуктивных токоприемников) подключить конденсатор (рис. 12, а), то угол сдвига фаз между током цепи и приложенным напряжением можно определить через его тангенс. Из треугольника проводимостей (рис. 12, г). tg φ = В данном примере в = в L —вс, где вL — реактивная проводимость индуктивной ветви; вс — реактивная проводимость емкостной ветви. Следовательно, в данном примере tgφ = Если в цепи вL>вc, то tgφ получится положительным, следовательно, и угол φ будет положительным. Это означает, что цепь носит индуктивный характер (рис. 78,6). На диаграмме вектор тока IР2 короче вектора Iр1, так как вL>вс. Поэтому ток I отстает от напряжения на угол φ. Если в цепи вc>вL, то tgφ отрицательный, то есть цепь носит емкостный характер (рис. 12, в). На диаграмме вектор тока Iр2 длинней, чем Iр1, так как вс>вL. Поэтому ток I опережает напряжение на угол φ. Как видно из этих диаграмм, величина и знак угла φ зависят от соотношения между реактивными проводимостями ветвей вL и вс- Если вL = вс то tgφ =
Следовательно, <φ = 0, значит цепь ведет себя, как активная (Рис. 12, г). При этом реактивная составляющая тока Iр=Uв=U0 = 0. Полный ток в цепи I=
Рис. 12. Резонанс токов: а — схема цепи; б, в и г — векторные диаграммы.
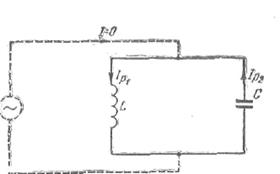
Рис. 13. Колебательный контур в цепи с переменной э. д. с.
Это обстоятельство объясняется тем, что реактивные токи в индуктивности и емкости по фазе не совпадают друг с другом на 180°, они всегда противоположны друг другу, и если в индуктивности в некоторый момент времени реактивный ток направлен от зажима А к зажиму В (рис 12, а), то в это время ток в емкости обязательно направлен от зажима В к зажиму А. Этот ток емкости, подойдя к точке А, оказывается тем источником зарядов, которые нужны для образования реактивного тока индуктивности, а реактивный ток индуктивности, подходящий к точке В, является источником зарядов, образующих ток емкости. Так как эти токи равны по величине, то они полностью обеспечивают друг друга и, генератору не требуется снабжать реактивным током ни индуктивные, ни емкостные ветви схемы. Другими словами, реактивные токи индуктивности и емкости текут за счет друг друга, в результате чего общий реактивный ток от генератора равен нулю. Явление совпадения по величине реактивных токов индуктивных и емкостных ветвей в параллельной цепи переменного тока называется резонансом токов. В режиме резонанса токов реактивные токи в ветвях могут оказаться очень большими и быть значительно больше тока всей цепи, текущего к ней от генератора. Такие соотношения могут быть, если активная проводимость цепи мала, а реактивные проводимости ветвей велики. Колебательный контур в цепи с переменной э. д. с. Если в режиме резонанса токов активная проводимость цепи уменьшится до нуля (при R1 = 0), то и активный ток ее окажется равным нулю, это значит, что в этом случае от генератора вообще никакой ток не течет, так как в режиме резонанса токов он состоит из одной активной составляющей (Iр = 0). Таким образом, переменные токи в ветвях (IР1 и IР2) существуют независимо от генератора, и его вообще можно отключить (рис. 13). Такую систему, состоящую из индуктивности и емкости, в которой может происходить колебательный процесс, назвали колебательным контуром, а колебания, происходящие в нем без помощи генератора,— свободными. Существование в контуре переменных токов IР1 и IР2 без помощи генератора — это и есть свободный колебательный процесс, но начавшийся под влиянием переменной э. д. с, а не порции энергии, внесенной заряженным конденсатором. Это также процесс обмена энергией между индуктивностью и емкостью. Не затухает он из-за отсутствия потерь энергии, поскольку в ветвях нет активных сопротивлений. В реальном колебательном контуре эти переменные токи без помощи генератора длительно существовать не могут. Частота свободных колебаний в контуре называется собственной частотой колебательного контура. Таким образом, колебательный контур представляет собой электрическую колебательную систему и в этом отношении подобен механической колебательной системе (маятнику), в которой тоже может совершаться свободный колебательный процесс, если ей сообщить некоторый запас энергии (толкнуть). Условием возникновения в цепи резонанса токов является равенство реактивных проводимостей индуктивной и емкостной ветвей, поэтому для получения его необходимо, изменяя емкость или индуктивность, добиться равенства вL и вс. Так как при изменении частоты индуктивная и емкостная проводимости изменяются взаимообратно, то даже при произвольных значениях индуктивности L и емкости С в цепи можно добиться - резонанса токов, подобрав частоту, при которой индуктивная проводимость вL окажется равной емкостной вс. Эту частоту называют резонансной и обозначают fрез. В идеальном колебательном контуре ее можно определить, имея в виду, что при этой частоте вL = вс. или Из этого условия
Следовательно, 4π2f2резLС=1, или f2рез = Окончательно
fрез =
где L — индуктивность контура (гн); С— емкость контура (ф); fрез—резонансная частота (гц).
В реальном колебательном контуре значение резонансной частоты несколько зависит и от величины активного сопротивления в нем. Резонансная частота обязательно равна собственной частоте колебательного контура. Если при произвольных индуктивности и емкости мы добьемся резонанса токов, подобрав частоту тока питающего генератора (например, fрез = 400 гц), то колебания в контуре будут совершаться с частотой 400 гц (в контуре будут течь переменные токи Ip1 и Ip2 с частотой 400 гц). Уменьшив активное сопротивление контура до нуля и отключив его от генератора, мы добьемся того, что колебания станут самостоятельными (свободными), но при этом частота их останется прежней (в контуре будут совершаться свободные колебания с частотой 400 гц), это значит, что собственная частота контура равна 400 гц. Если цепь питается от генератора, создающего ток с частотой 50 гц, а резонанса мы добиваемся, изменяя вL или вс, то тем самым мы подбираем такую индуктивность или такую емкость, при которых собственная частота контура оказывается равной 50 гц (вL = вс при частоте 50 гц). На основании этих рассуждений, формула резонансной частоты позволяет подсчитывать собственную частоту колебательного контура. Из нее следует, что собственная частота контура зависит от величины индуктивности и емкости и чем они больше, тем собственная частота меньше. Из уравнения 2πfрез = = Таким образом, резонанс токов — это явление, возникающее в параллельных цепях переменного тока при совпадении частоты тока питающего генератора с собственной частотой колебательного контура, а добиваются его двумя путями: либо собственную частоту контура подгоняя под частоту питающего тока (изменяя параметры контура), либо частоту питающего тока подгоняя под собственную частоту контура. Компенсация сдвига фаз Так как всякая реактивная мощность создается реактивным током, то емкость, являясь источником реактивного тока для индуктивности, оказывается для нее и источником реактивной мощности. Поэтому после подключения емкости к цепи обмен энергией происходит не между индуктивностью и генератором, а между индуктивностью и емкостью. Если емкость недостаточно большая, то ток ее меньше реактивного тока индуктивности, и генератор освобожден от него не полностью (цепь ведет себя как индуктивная). Если емкость слишком большая, то ее ток больше реактивного тока индуктивности и генератор загружен, емкостным реактивным током (цепь, потребляя емкостный ток, ведет себя как цепь емкостная). Эти обстоятельства можно использовать для компенсации сдвига фаз, создаваемого индуктивной нагрузкой (электродвигателями), то есть для увеличения cos φ. Для компенсации сдвига фаз достаточно параллельно индуктивной нагрузке подсоединить емкость с таким расчетом, чтобы ток емкости был равен реактивному току нагрузки и генератор оказался полностью освобожденным от реактивного тока и реактивной мощности. Пример. Электрический двигатель мощностью 1,0 квт работает с коэффициентом полезного действия η = 0,83 и cos φ = 0,5. Подсчитать емкость конденсатора, который нужно подключить к сети параллельно двигателю для того, чтобы полностью скомпенсировать сдвиг фаз, создаваемый двигателем. Напряжение сети 380 в. Решение. Мощность, потребляемая двигателем из сети,
Р=
Реактивный ток двигателя Iр=Isin φ = 6,3 · 0,865=5,45 а. Следовательно, для полной компенсации сдвига фаз и обеспечения двигателя реактивным током ёмкостной ток I с должен быть равен 5,45 а.
Емкостное сопротивление конденсатора Хс = Емкость конденсатора
C=
При частичной компенсации емкость разгружает генератор от реактивного тока не полностью. Величину необходимой при этом емкости определяют в зависимости от величины тока, который должна обеспечить емкость. Для этого определяют реактивный ток Iр1 нагрузки до компенсации, реактивный ток Iр2 от источника тока после компенсации и реактивный ток Iр, который должна обеспечить емкость. Очевидно IP = IP1 – IP2. По величине тока Iр определяют емкость конденсатора так же, как и при полной компенсации. Пример. Определить емкость конденсатора, который необходим для увеличения cos φ до значения 0,9 в условиях, приведенных в предыдущем примере. Решение. Реактивный ток двигателя до компенсации Ip1=5,45 а. Полный ток двигателя после компенсации
I2 = Реактивный ток двигателя после компенсации
IР2 =I2 sin φ2 = 3, 5·0,435 = 1,53а
Реактивный ток, который должен поступать в двигатель от конденсатора, IP=IP1 – IP2 =5.45a – 1.53a = 3.92a
Емкостное сопротивление конденсатора
Xc =
Емкость конденсатора
C = Сравнив результаты этого и предыдущего примеров, мы видим, что для увеличения соs φ всего на 0,1 (с 0,9 до 1,0) емкость необходимо увеличить почти в полтора раза, поэтому практически полной компенсации добиваться нецелесообразно (емкость увеличивается сильно, а эффект от этого небольшой). Обычно cos φ увеличивают до значения 0,85—0,9. Кроме того, для различных категорий нагрузок устанавливается так называемый штрафной cos φ. Если на предприятии cos φ ниже штрафного, то к предприятию применяют меры экономического воздействия (штрафы, увеличение стоимости энергии и другие). При использовании конденсаторов, специально предназначенных для компенсации сдвига фаз, расчет целесообразно вести по реактивной мощности, которую конденсаторы могут отдать индуктивной нагрузке при рабочем напряжении, на которое они рассчитаны. Рабочее напряжение и реактивная мощность, которую может отдать конденсатор, записаны на самом конденсаторе.
Технологическая карта№8 Измерение работы и мощности в цепи однофазного переменного тока. Цель работы – ознакомиться с приборами (счетчиком и ваттметром), применяемыми для учета электроэнергии и измерения мощности, потребляемой в цепи однофазного переменного тока, а так же со схемами их включения.
Оборудование и аппаратура Амперметр переменного тока на 5 А 1 шт Вольтметр переменного тока на 150 В 1 шт Однофазный фазометр на 127 В, 5 А 1 шт Однофазный ваттметр на 127 В, 5 А 1 шт Счетчик активной энергии однофазный СО на 127 В, 5 А 1 шт Потенциометр на 250 Ом, 0,5 А 1 шт Реостат регулировочный на 20 Ом, 4 А 1 шт Панель с четырьмя потолочными патронами 1 шт Лампы накаливания на 127 В, 150 Вт 4 шт Рубильник двухполюсный на 127 В, 60 А 1 шт Катушка индуктивности на 3 А 1 шт Провода соединительные многожильные площадью сечения 2,5 мм2, длинной 1,5 м 14 шт Источник переменного тока на 127 В, 50 Гц Порядок выполнения работы 1. Ознакомиться с устройством счетчика и ваттметра и схемами их включения. 2.
Включить измерительные приборы в соответствии со схемой, показанной на рис. 14.
Рис 14. Схема соединений приборов для измерения мощности и энергии в однофазной цепи переменного тока и для поверки электрических счётчиков.
3. Измерить мощность, силу тока и напряжение. (Показания счетчика записывают в начале опыта и по истечении 10 мин. Нагрузка – чисто активная – лампа накаливания). Результаты записать в таблицу. Измерения выполнить при различном количестве ламп. 4. Повторить испытания при нагрузке, состоящей из индуктивной катушки и активного сопротивления. Результаты испытаний записать в таблицу. Измерения выполнять при различных силах тока. 5. Собрать схему, показанную на рис. 16, нате же нагрузки и проверить потребляемую мощность с помощью трех приборов. 6. Составить отчет.
Содержание отчета 1. Наименование отчета. 2. Параметры измерительных приборов и оборудования. 3. Схемы включения счетчика, ваттметра, амперметра и вольтметра для измерения мощности и электрической энергии. 4. Таблица с результатами измерения активной мощности и электрической энергии в цепи однофазного переменного тока. 5. Схема включения трех электроизмерительных приборов (амперметра, вольтметра и фазометра) для измерения мощности. 6. Выводы.
Дополнительный материал к работе. Электрической энергией называется работа, выполняемая электрическим током в течение какого-либо отрезка времени. Электрическую энергию измеряют электрическим счетчиком и определяют как произведение активной электрической мощности Р на время t:
W = Pt
За единицу энергии принят один джоуль (Дж): 1 Дж = 1 Вт х 1 с. Джоуль очень маленькая единица, поэтому в практике пользуются единицей в 3 600 000 раз большей – 1 кВт.ч. В этом случае активную электрическую мощность Р измеряют в киловаттах, а время t – в часах. 1 кВт/ч энергии равен 367 200 кгс.м, или 860 ккал. Электрическая мощность определяется как работа, совершенная электрическим током в единицу времени, и за единицу ее принят 1 Вт = 1 Дж/ 1с. при переменном однофазном токе полную электрическую мощность измеряют в вольт-амперах (В .А) и определяют по формуле
S = UI,
где U – действующее напряжение, В; I - действующая сила тока, А. активную электрическую мощность однофазного переменного синусоидального тока измеряют в ваттах (Вт) и определяют по формуле
P = IU cos φ = I2r
Если приемники электрической энергии создают магнитное или электрическое поле, как, например, электродвигатели, сварочные трансформаторы и другие подобные установки, то кроме активной мощности в этом случае к потребителю электрического тока подводится реактивная мощность, которую обозначают Q, измеряют в вольт-амперах реактивных (ВАр) и определяют по формуле
Q = IU sin φ = I2x
Если известны активная и реактивная мощности, подводимые к потребителям электрической энергии, можно определить полную мощность электрической цепи, представляющую собой их геометрическую сумму
Полную электрическую мощность можно измерить при помощи вольтметра и амперметра. Измерять активную мощность в цепи однофазного переменного тока можно двумя методами: включением в цепь специального электроизмерительного прибора – ваттметра (рис. 15) или трех электроизмерительных приборов – вольтметра, амперметра и фазометра (рис. 16). Во втором случае мощность подсчитывают перемножением показаний всех трех приборов.
Рис 15Схема включения Рис 16Схема включения приборов однофазного ваттметра. для измерения мощности в цепи однофазного переменного тока.
Ваттметр снабжен двумя катушками: токовой, включаемой последовательно с потребителями, по которой проходит весь измеряемый ток (точно так же, как по катушке амперметра), и напряжения с добавочным сопротивлением, которая включена так же, как вольтметр, т.е. показания ваттметра – это произведение трех величин: напряжения U, силы тока I и коэффициента мощности cos φ. При подключении зажимов ваттметра к измеряемой цепи необходимо соединить начала и концы его обмоток в соответствии с направлением электрической энергии от генерирующей станции к потребителю. Начала (генераторные зажимы) ваттметров обозначают звездочкой. Если нарушить этот порядок, стрелка ваттметра будет отклоняться в противоположную сторону.
Технологическая карта№9
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.109 (0.015 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||

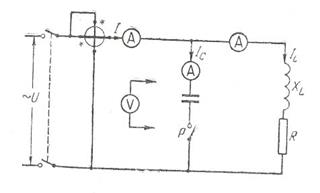
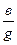
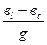
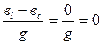
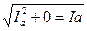 По величине он минимален, так как в нем полностью отсутствует реактивная составляющая и он равен своей активной составляющей. Несмотря на то, что от генератора течет ток, не содержащий реактивной составляющей, реактивные токи в ветвях есть (IР1=UВL И IР2 = Uвс).
По величине он минимален, так как в нем полностью отсутствует реактивная составляющая и он равен своей активной составляющей. Несмотря на то, что от генератора течет ток, не содержащий реактивной составляющей, реактивные токи в ветвях есть (IР1=UВL И IР2 = Uвс).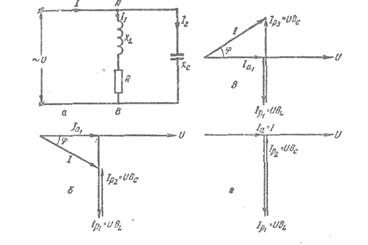
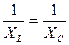
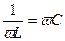 , или 1=ωLC
, или 1=ωLC 
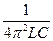
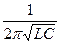
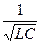 , но так как к 2πfрез =ω0, то ω0 =
, но так как к 2πfрез =ω0, то ω0 = 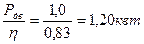
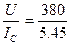 = 69,7 ом.
= 69,7 ом.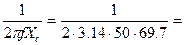 0.0000456 ф, или С= 45,6 мкф
0.0000456 ф, или С= 45,6 мкф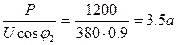 , sinφ2 =
, sinφ2 = 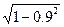 = 0.435
= 0.435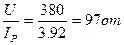
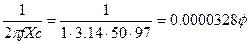 , или С = 32,8 мкф
, или С = 32,8 мкф