Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства сумм линейных напряжений и линейных токов.
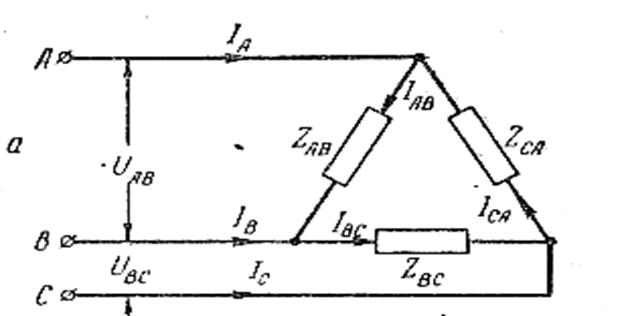
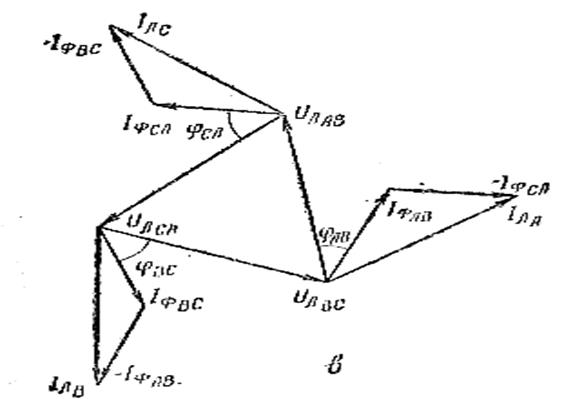
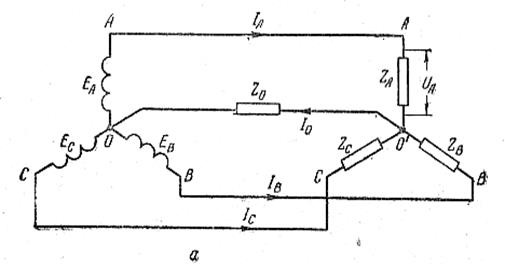
В трехфазной системе, соединенной звездой или треугольником, в любой момент времени мгновенные значения линейных напряжений равны разности потенциалов соответствующих проводов в этот же момент времени. Поэтому для схемы
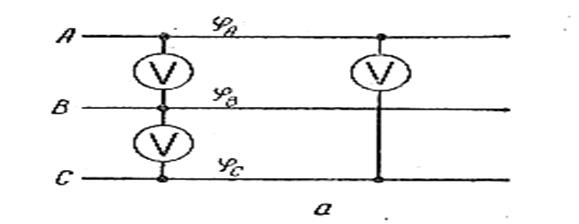
иАВ = φ А – φ В; иВС = φ В - φ С; иСА = φ С - φ А, где, φ – потенциал соответствующего провода. Сумма линейных напряжений иАВ + иВС + иСА = φ А - φ В + φ В - φ С + φ С - φ А = 0, то есть алгебраическая сумма мгновенных значений линейных напряжений равна нулю. Если оперировать действующими значениями, то сумма должна быть геометрической Ū АВ + Ū ВС + Ū СА = 0, или Ů АВ + Ū ВС + Ū СА = 0. Из этих формул следует, что, если линейные напряжения заданы векторами, они обязательно образуют замкнутый треугольник,
так как замыкающая, проведенная из начала первого вектора до конца последнего, представляет собой сумму этих векторов, а в данном случае эта сумма равна нулю, а значит, равна нулю и замыкающая. Следовательно, конец последнего вектора обязательно попадает в начало первого. Это свойство используется при анализе явлений в цепях. Кроме того, имея в виду это свойство, можно с помощью трех вольтметров, измеряющих линейные напряжения, определить углы сдвига фаз между ними.
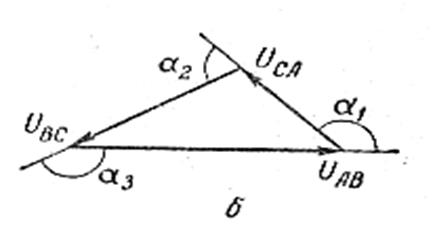
Для этого, задавшись удобным масштабом, по показаниям приборов, как по трем сторонам, строим замкнутый треугольник.
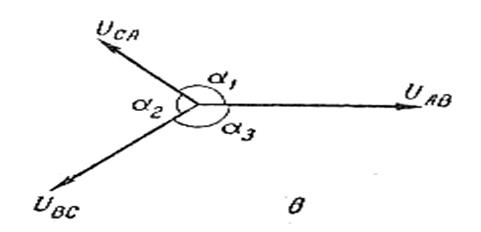
Внешние углы его а и будут углами сдвига фаз между линейными напряжениями. Для большей наглядности после построения треугольника векторы можно перенести параллельно самим себе, так, чтобы они оказались проведенными из одной точки.
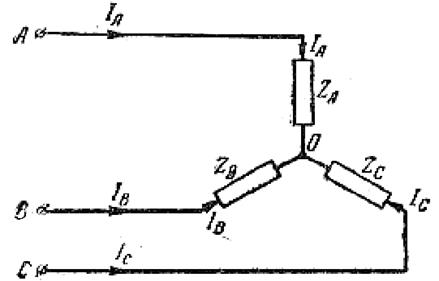
Если нагрузка соединена звездой,
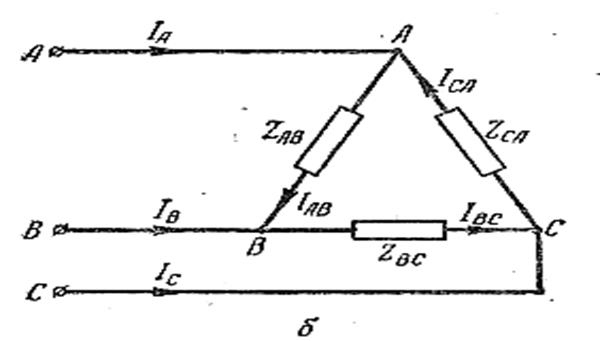
то на основании первого правила Кирхгофа, для узла О ĺ ф А + ĺ ф В +ĺ ф С = 0, поэтому ĺА + ĺ В + ĺ С = 0, Ī А + Ī В + Ī С = 0. При нагрузке, соединенной треугольником,
для узлов А, В и С по первому правилу Кирхгофа, ĺА = ĺАВ - ĺСА + ĺВ = ĺВС - ĺАВ ĺС = ĺСА - ĺВС ∑ ĺл = ĺАВ – ĺСА + ĺВС - ĺАВ + ĺСА – ĺВС = 0, _____ ∑ ĺл = 0__и___ ∑ Īл = 0. Таким образом, в трехпроводной системе как при соединении звездой, так и при соединении треугольником геометрическая сумма действующих значений линейных токов равна нулю. Это свойство линейных токов также имеет теоретическое и практическое значение. Например, только благодаря этому свойству трехфазный ток можно передавать по кабелю с металлической оболочкой, так как при близком расположении проводов в кабеле результирующее поле вокруг них очень слабое и в оболочке вихревые токи почти не наводятся.
Если трехжильный кабель, использовать как одножильный, соединив три жилы параллельно, то металлическую оболочку с кабеля придется снять, так как в этом случае _ ∑ ĺл ≠ 0 и вокруг такой тройной жилы будет сильное магнитное поле, которое наведет в оболочке сильные вихревые токи и кабель перегреется. Неравномерная нагрузка фаз. Соединение звездой. При неравномерной нагрузке фаз, когда I А ≠ I В ≠ I С , в нулевом проводе трехфазной системы, соединенной звездой, течет уравнительный ток I 0.
Но ток в участке цепи может течь лишь в том случае, когда на его концах есть разность потенциалов. Следовательно, при неравномерной нагрузке фаз между точками О и О′ возникает разность потенциалов (напряжение). Напряжение между нулевыми точками генераторов и нагрузки называют смещением нейтрали (U 0 ). Из схемы U 0 = I 0 z 0, где z 0 – сопротивление нулевого провода. Смещение нейтрали оказывает сильное влияние на работу нагрузки. По второму правилу Кирхгофа, для контура ОАА′О′О Ė А = Ů А = Ů 0, откуда Ů А = Ė А - Ů 0. Рассуждая совершенно аналогично для контуров ОВВ′О′О и ОСС′О′О, получим подобные выражения для Ů В и Ů С.
Ů В = Ė В - Ů 0; Ů С = Ė С - Ů 0. Построим векторную диаграмму этих величин. Для этого отложим векторы фазных э. д. с., которые равны по величине и направлены под углом 1200 друг к другу, и вектор смещения нейтрали, который тоже имеет некоторые величину и направление.
Из формулы Ė А = Ů А = Ů 0 следует, что Ē А можно получить, если к Ū 0 пристроить Ū А, а из диаграммы видно, что для получения Ē А к Ū 0 надо пристроить отрезок О′А. Следовательно, этот отрезок и будет выражать Ū А. Рассуждая аналогично в отношении э. д. с. Е В и Е С, придем к выводу, что отрезок О′В изображает Ū В, а отрезок О′С изображает Ū С.
Из этой диаграммы видно, что напряжения на фазах оказываются неодинаковыми, наступает так называемый перекос фазных напряжений. Перекос фазных напряжений – явление весьма нежелательное, оно нарушает работу отдельных фаз. Из этой же диаграммы следует, что причиной перекоса является смещения нейтрали, и чем больше Ū 0, тем разница между фазными напряжениями больше, чем меньше Ū 0, тем фазные напряжения более симметричны, и если Ū 0 = 0, то точка О′ сольется с О и фазные напряжения станут совершенно одинаковы. Следовательно, при эксплуатации трехфазных систем надо стремиться к тому, чтобы смещение нейтрали было возможно меньше. Из формулы U 0 = I 0 z 0 следует, что для уменьшения U 0 надо уменьшать либо I 0, либо z 0. Уменьшить уравнительный ток I 0 можно, выравнивая нагрузку фаз. Если это по каким-либо причинам невозможно, а смещение нейтрали слишком велико, то надо уменьшать сопротивление нулевого провода z 0, то есть увеличивать его сечение, железный провод заменять алюминиевым или медным. Если потенциал нулевой точки генератора принять равным нулю и посчитать, что на диаграмме ей соответствует точка О, то любая другая точка на этой диаграмме будет соответствовать совершенно определенной точке цепи и отрезок, соединяющий две любые точки на диаграмме, будет определять по величине и фазе напряжения между соответствующими точками цепи. Такая диаграмма, любая точка которой соответствует определенной точке цепи, называется топографической. На рисунке
точка О′ соответствует нулевой точке нагрузки, точки А, В и С – точкам А, В, и С цепи, отрезок ОО′ отображает смещение нейтрали, отрезки АВ, ВС и СА – линейные напряжения U АВ, U ВС, U СА и т.д. Расчет трехфазной системы, соединенной звездой. Под расчетом трехфазной системы подразумевают определение фазных и линейных токов, фазных напряжений, потребляемой мощности, коэффициента мощности, а при необходимости и ряда других величин. При этом заданными обычно являются фазные э. д. с. источника тока, его внутреннее сопротивление, сопротивления проводов и фаз нагрузки. Трехфазная система, соединенная звездой, представляет собой цепь с двумя узловыми точками. Следовательно, трехфазную систему, соединенную звездой, можно рассчитывать методом узлового напряжения, только оперировать следует не абсолютными значениями величин, а их комплексными выражениями. Попытка определить фазные токи (а следовательно, и линейные) по формуле I Ф = U Ф z приведет к неверным результатам, так как при неравномерной нагрузке фаз фазные напряжения неодинаковы и нам не известны. Порядок расчета лучше всего проследить на примере. Пример. Определить линейные токи и напряжения на фазах нагрузки, которая питается от трехфазного генератора, с фазными э. д. с. Е Ф = 220 в и внутренним сопротивлением Х Lо = 1 ом, если сопротивления фазных проводов чисто активные, R пр = 2 ом, сопротивление нулевого провода Z о = (1+ j2) Ом, а сопротивление фаз нагрузки выражается комплексами: Z А = (3 + j4) ом, Z В = (6 + j5) ом, Z С = (5 + j6) О м
Решение. Выразим фазные э. д. с. в комплексной форме. Направим Ē А по действительной оси, тогда Ė А = 220 в, Ė В = 220е-j120о = 220 (- 0,5 – j 0,87) = (- 110 – j 192) в, Ė С = 220е120о = 220 (- 0,5 + j 0,87) = (- 110 + j 192) в. «Внесем» внутренние сопротивления фаз генератора и сопротивления фазных проводов в нагрузку. Сопротивление и проводимость фазы нагрузки с «внесенными» туда сопротивлениями обозначим знаком штрих. Z′ А = Z А + jХ Lо + R пр = 3 + j 4 + j 1 + 2 = (5 + j5) ом; Z′ В = Z В + jХ Lо + R пр = 6 + j 5 + j 1 + 2 = (8 + j6) ом; Z′ С = Z С + jХ Lо + R пр = 5 + j 6 + j 1 + 2 = (7 + j7) ом. Определим проводимость ветвей: Y′А = _ 1_ = _1__ = (0,1 – j 0,1) сим; Z′ А 5 + j 5 Y′В = _ 1_ = _1__ = (0,08 – j 0,06) сим; Z′ В 8 + j 6 Y′С = _ 1_ = _1__ = (0,07 – j 0,07) сим; Z′ С 7 + j 7 Y′0 = _ 1_ = _1__ = (0,2 – j 0,4) сим. Z 0 1+ j 2 Определяем смещение нейтрали (узловое напряжение): Ů 0 = ĖАY ′ А _+_ ĖВY ′ В _+ ĖСY ′ С = Y ′ А + Y ′ В + Y ′ А + Y0 = 220 (0,1 – j 0,1) + (- 110 – j192) ∙ (0,08 – j 0,06) + (- 110 + j192) ∙ (0,07 – j 0,07) = 0,1 - j 0,1 + 0,08 – j 0,06 + 0,07 – j 0,07 + 0,2 – j 0,4 = 15,7 + j 0,6 ≈ 15,7 в. Находим токи в ветвях (линейные токи): İ А = (ĖА - Ů 0) Y ′ А = (220 – 15,7) (0,1 – j 0,1) = (20, 43 – j 20,43) а; İ В = (ĖВ – Ů 0) Y ′ В = (- 110 – j 192 – 15,7) (0,08 – j 0,06) = (- 21,5 – j 7,8) а; İ С = (ĖС – Ů 0) Y ′ С = (- 110 – j 192 – 15,7) (0,07 – j 0,07) = (- 21,13 + j 4,67) а, то есть I А = √ 20,432 + 20,432 = 28,6 а; I В = √21,52 + 7,82 = 22,9; I С = √22,132 + 4,672 = 22,6 а Определяем напряжение на фазах: Ů А = İ А Z А = (20,43 – j 20,43) (3+ j 4) = (143 + 20,4) в; Ů В = İ В Z В = (- 21,5 – j 7,8) (6 + j 5) = (-89,8 – j 154,3) в; Ů С = İ С Z С = (- 22,13 – j 4,67) (5 + j 6) = (-139,2 – j 109,5) в, или U А = √1432 + 20,412 ≈ 144 в; U В = √89,82 + 154,32 = 178 в; U С = √139,22 + 109,52 = 177 в По полученным данным можно найти все остальные величины (мощности, линейные напряжения на нагрузке, падение напряжения в линии и т.п.).
Нагрузку, работающую без нулевого провода, рассчитываю так же, но в знаменателе уравнения U 0 отсутствует слагаемое Y 0 (Y 0 = 0): Ů 0 = Ė А Y′ А + Ė В Y′ В + Ė С Y′ С Y′ А + Y′ В + Y′ С Часто приходится определять линейные токи и другие параметры нагрузки, когда заданы сопротивления ее фаз и линейное напряжение в сети, к которой подсоединена нагрузка. При этом сопротивления проводов могут быть заданы, а могут быть неизвестны. В этом случае заданное линейное напряжение считают линейным напряжением воображаемого генератора, соединенного звездой, с внутренним сопротивлением, равным нулю,
и расчет опять ведут по методу узлового напряжения. При этом в качестве фазных э.д.с. используют фазные напряжения, подсчитанные по заданному линейному. Пример. Три активных сопротивления R А, R В, , R Ссоединены звездой без нулевого провода и подсоединены к щиту, линейное напряжение на зажимах А, В и С которого 380 в. Определить напряжения на фазах и линейные токи этой нагрузки, если R А = 20 ом; R В = 20 ом; R С = 5 ом. Решение. Считаем зажимы А, В и С зажимами генератора, соединенного звездой, тогда Е А = Е В = Е С = 380 = 220 в √3 Ė А = 220 в, Ė В = 220 е - j 120о = (-110 – j 192) в; Ė С = 220 е - j 120о = (-110 – j 192) в Так как нагрузка чисто активная, то Z А = R А + j 0 = 20 + j 0 = 20 ом, Z В = 10 ом, Z С = 5 ом. Сопротивление подводящих проводов не заданы, значит, ими можно пренебречь, внутреннего сопротивления у воображаемого генератора нет, поэтому Y А = _1_ = _1_ = 0,05 сим; Y В = _1_ = _1_ = 0,1 сим; Y С = _1_ = _1_ = 0,2 сим Z А 20 Z В 10 Z С 5 Так как нагрузка работает без нулевого провода, то Z 0 = ∞ и Y 0 = 0. Тогда
Ů 0 = Ė А Y А + Ė В Y В + Ė С Y С = Y А + Y В + Y С = 220 ∙ 0,05 + (- 110 - j 192) 0,1 + (- 110 + j 192) 0,2 = (-62,8 + j 54,8) в. 0,05 + 0,1 + 0,2 Линейные токи İА = (Ė А - Ů 0) Y А = (220 + 62,8 - j 54,8) 0,05 = (14,1 – j 2,74) а; İВ = (Ė В - Ů 0) Y В = (- 110 - j 192 + 62,8 - j 54,8) 0,1 = (- 4,72 - j 24,68) а; İС = (Ė С - Ů 0) Y С = (- 110 - j 192 + 62,8 - j 54,8) 0,1 = (- 4,72 + j 27,4) а; или İА = √ 14,12 + 2,742 = 14,2 а; İВ = √ 4,722 + 24,682 = 25,1 а; İС = √ 9,442 + 27,42 = 29 а.
Ů А = Ė А - Ů 0; Ů В = Ė В - Ů 0; Ů С = Ė С - Ů 0.
Ů А = Ė А - Ů 0 = 220 + 62,8 - j 54,8 = (282,8 - j 54,8) в; Ů В = Ė В - Ů 0 = (-110 - j 192) + 62,8 - j 54,8 = (-47,2 – j 246,8) в; Ů С = Ė С - Ů 0 = (-110 + j 192) + 62,8 - j 54,8 = (-47,2 + j 137,2) в, или U А = √ 282,22 + 54,82 = 288 в; U В = √ 47,22 + 246,82 = 252 в; U С= √ 472 + 137,22 = 145 в. Из этого примера видно, насколько велика роль смещения нейтрали и насколько несимметричными могут быть из-за этого фазные напряжения. Все варианты симметричной нагрузки, соединенной звездой, можно рассчитывать тоже по методу узлового напряжения, но при симметричной нагрузке смещение нейтрали отсутствует (U 0 =0), поэтому все фазные напряжения равны друг другу и І л = І ф = U ф = U л_ __, z √ 3 z где z – сопротивление одной фазы нагрузки.
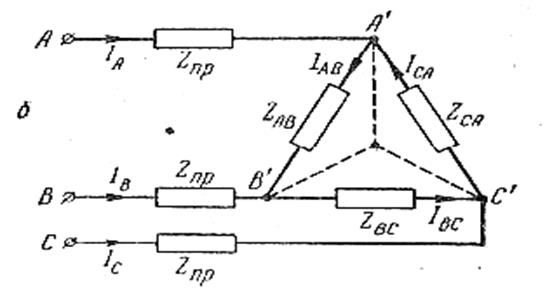
При этом если сопротивления фазных проводов и внутренние сопротивления генератора надо учитывать, то их надо «внести» в сопротивление фаз нагрузки и І л = U л_ __, √ 3 z ′ Соединение треугольником. При соединении неравномерной нагрузки треугольником
явлений, подобных смещению нейтрали и перекосу фазных напряжений, не наблюдается, но неравномерная нагрузка фаз вызывает неравенство линейных токов и неодинаково нагружает фазы генератора. Из-за этого падения напряжения в отдельных проводах и на внутренних сопротивлениях фаз генератора несколько отличаются друг от друга, поэтому и фазные напряжения оказываются неодинаковыми. Но это неравенство незначительно и при правильном выборе проводов оно настолько мало, что им пренебрегают и считают, что неравномерность нагрузки на фазных напряжениях не отражается. Расчет нагрузки, соединенной треугольником. При этом следует рассмотреть два основных случая: а) сопротивлением подводящих проводов и внутренним сопротивлением генератора можно пренебречь; б) указанными сопротивлениями пренебрегать нельзя. Когда сопротивлением фазных проводов и внутренним сопротивлением генератора можно пренебречь, напряжения на фазах нагрузки равны линейному напряжению генератора или сети, к которой эта нагрузка присоединяется, поэтому по заданному линейному напряжению и сопротивлению фаз нагрузки определяют фазные токи, а по ним и линейные токи как геометрические разности соответствующих фазных. Пример. Определить линейные токи и активную мощность нагрузки, присоединенной к сети с линейным напряжением 380 в, если сопротивления ее фаз Z АВ = (3 + j 4) ом; Z ВС = (16 + j 12) ом; Z СА = (7 + j 7 ) ом. Решение. Направим вектор линейного напряжения U АВ по действительной оси, тогда Ů АВ = 380 в; Ů АВ = 380 е - j 120о = 380 (- 0,5 – j 0,87) = (- 190 – j 331) в; Ů АВ = 380 е j 120о = (- 190 – j 331) в. Сопротивления фаз в показательной форме Z АВ = 3 + j 4 ≈ 5 е j 53о ом; Z ВС ≈ 20 е j 37о ом; Z СА ≈ 10 е j 45о ом. Фазные токи İ АВ = Ů АВ = 380 = 76 е - j 53о = (45,7 – j 60,9) а; Z АВ 5еj 53о
İ ВС= Ů ВС = 380 е – j 120о = 19 е- j 157о = (- 17,5 – j 7,4) а; Z ВС 20 е j 37о
İ СА= Ů СА = 380 е j 120о = 38 е j 75о = (9,81 + j 36,3) а. Z ВС 10 е j 45о Так как фазные токи неодинаковы, то линейные приходится находить, как разность соответствующих фазных: İ А = İ АВ - İ СА = 45, 7 – j 60,9 – 9,81 – j 36,3 = (35,89 – j 97,2) а; İ В = İ ВС - İ АВ = - 17,5 – j 7,4 – 45,7 + j 60,9 = (- 63,20 + j 53,5) а; İ С = İ СА – İ ВС = 9,81 + j 36,3 + 17,5 + j 7,4 = (27,31 + j 43,7) а. или І А = √ 35,892 + 97,22 = 103,8 а; І В = √ 63,302 + 53,52 = 82,8 а; І С = √ 27,312 + 43,72 = 51,6 а. Фазные мощности: Š АВ = Ů АВ Ĩ АВ = 380 (45,7 + j 60,9) = (17 400 + j 23 150) ва; Š ВС = Ů ВС Ĩ ВС = (- 190 + j 7,4) = (5780 + j 4390) ва; Š СА = Ů СА Ĩ СА = (- 190 + j 331) (9,81 – j 36,3) = (10 180 + j 10 145) ва.
Активная мощность всей цепи Р = Р АВ + Р ВС + Р СА = 17 400 + 5780 + 10 180 = 33 360 вт. Если нагрузка симметрична, то фазные токи одинаковы, расчет значительно упрощается и его можно провести без использования комплексных чисел. І Ф = U л; І л = І Ф √ 3, а Р = √ 3 U л І л cos φ. z Если сопротивлениями подводящих проводов или внутренним сопротивлением фаз генератора пренебречь нельзя,
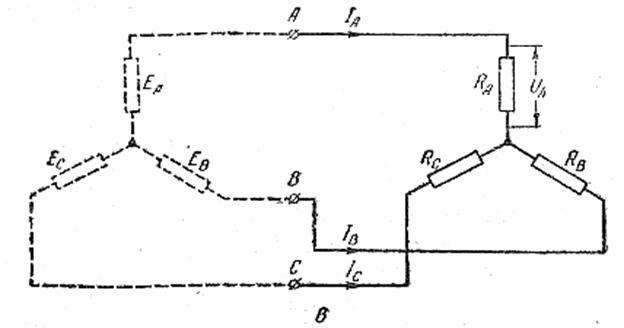
То сопротивления проводов Z пр и внутреннее сопротивление фаз генератора (если оно задано) надо «внести» в фазы нагрузки, а для этого треугольник следует заменить эквивалентной звездой и «вносить» их уже в фазы звезды. Затем решать цепь так, как ее решают при соединении нагрузки звездой. Пример. Определить линейные токи нагрузки, изображенной на рисунке, если она питается от сети с U л = 380 в, причем Ż АВ = (7 + j 7) ом, Ż ВС = 10 ом; Ż СА = 20 ом; Ż пр = 2 ом. Решение. Треугольник А΄В΄С΄ преобразуем в эквивалентную звезду Z А = __ Z АВ ZС А____ = _ (7 + j 7)· 20_ = (7 + j 7)· 20 = (4,73 + j 3,35) ом; Z АВ + Z ВС + ZС А 7 + j 7 + 10 + 20 37 + j 7 Z В = __ Z АВ Z ВС____ = _ (7 + j 7)· 10 = (2,365 + j 1,675) ом; 37 + j 7 37 + j 7
Z С = __ ZС А Z ВС____ = 20 · 10_ = (5,2 - j 0,982) ом. 37 + j 7 37 + j 7 Внесем сопротивления проводов в фазы звезды: Z ΄А = Z А + Z пр = 4,73 + j 3,35 + 2 = (6,73 + j 3,35) ом; Z ΄В = Z В + Z пр = 2,365 + j 1,675 + 2 = (4,365 + j 1,675) ом; Z ΄С = Z С + Z пр = 5,2 – j 0,982 + 2 = (7,2 – j 0,982) ом. Э. д. с. воображаемого генератора Е Ф = 380 = 220 в √ 3 Направим Ē А по действительной оси, тогда Ė А = 220 в. Ė В = 220 е – j 120о = = (- 110 – j 192) в; Ė С = 220 е j 120о = (- 110 + j 192) в. Проводимость ветвей: Y ΄А = _1_ = _ ___1_____ = (0,119 - j 0, 059) сим; Z ΄А 6,73 + j 3,35 Y ΄В = _1_ = _ ___1_______ = (0,2 - j 0,0765) сим; Z ΄В 4,365 + j 1,675 Y ΄С = _1_ = _ ___1_______ = (0,1795 + j 0,0338) сим. Z ΄С 5,2 – j 0,982 Узловое напряжение Ů 0 = Ė А Y ΄А + Ė В Y ΄В + Ė С Y ΄С = Y ΄А + Y ΄В + Y ΄С = 220 (0,119 – j 0,059) + (-110 – j 192) (0,2 – j 0,0765) + (-110 + j 192) (0,1795 + j 0,0338) = 0,119 – j 0,059 + 0,2 – j 0,0765 + 0,1795 + j 0,0338 = (-21,2 – j 64,3) в. Линейные токи: İ А = (Ė А - Ů 0) Y ΄А = (220 + 21,2 + j 64,3) (0,119 – j 0,059) = (33,5 – j 6,6) а; İ В = (Ė В - Ů 0) Y ΄В = (- 110 – j 192 + 21,2 + j 64,3) (0,2 – j 0,0765) = (-27,6 – j 18,7) а; İ С = (Ė С - Ů 0) Y ΄С = (-110 + j 192 + 21,2 + j 64,3) (0,1795 + j 0,0338) = (-26,67 + j 43) а. или I А = √ 33,52 + 6,62 = 34,2 а; I В = √ 27,62 + 18,72 = 33,3 а; I С = √ 24,672 + 432 = 50,6 а. Если нагрузка будет симметричной, то решение будет отличаться тем, что после преобразования треугольника в звезду и «внесения» в нее сопротивлений проводов, нет надобности заканчивать решение методом узлового напряжения, так как звезда будет симметричной, напряжения на ее фазах будут одинаковые и их можно подсчитать по заданным линейным напряжениям. Последовательность фаз. Токи трехфазной системы сдвинуты относительно друг друга по фазе на угол 1200, поэтому максимума они достигают не одновременно, а в разные моменты времени. Порядок, в котором проходят через положительный максимум токи трехфазной системы, называют последовательностью фаз. Фазы обычно обозначают буквами А, В и С. если максимум наступает в первую очередь в фазе А, затем в фазе В, а потом в фазе С,
то такую последовательность называют прямой. Если же после фазы А, максимум наступает в фазе С, а уж потом в фазе В,
то такую последовательность называют обратной. Так как процесс чередования максимумов повторяется, и после фазы С максимума снова наступает в фазе А, то любую фазу можно принять за первую, и ответ на вопрос, какая из оставшихся двух фаз является второй, а какая третьей, зависит от последовательности. На рисунке, за первую принята фаза В, затем максимум наступает в фазе А и в последнюю очередь – в фазе С.
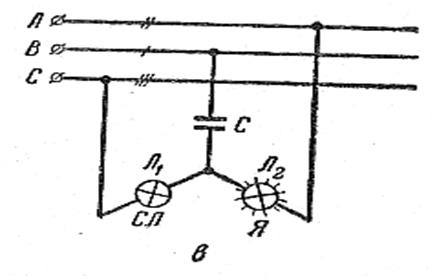
Написав подряд два раза этот порядок чередования фаз и начавсчет с фазы А, мы определим последовательность. В данном случае В АСВ АС. Начиная счет с фазы А, получаем обратную последовательность АВС (подчеркнуто). Если бы после фазы В максимума наступал в фазе С, то последовательность была бы прямой ВС АВС А. Кроме того, в этой сети последовательность можно сделать прямой и при прежнем порядке чередования (сначала в средней, затем в верхней, потом в нижней), если фазу А обозначить С, а фазу С обозначить А. тогда после фазы В максимум наступает в фазе С (бывшая А), а потом в А (бывшая С) и последовательность окажется прямой (ВС АВС А). Таким образом, последовательность фаз зависит от порядка чередования максимумов и обозначения шин, проводов или зажимов. Последовательность фаз в системе имеет большое значение, так как от нее зависит направление вращения трехфазных двигателей, способ включения измерительных приборов при измерениях в трехфазных цепях. Последовательность фаз надо знать при включении на параллельную работу трехфазных генераторов, трансформаторов и в ряде других случаев. Приборы, которые служат для определения последовательности фаз, называются фазоуказателями. В настоящее время наибольшее применение нашли фазоуказатели двух типов: ламповый и фазоуказатель ФУ – 2. Ламповый фазоуказатель представляет собой несимметричную звезду без нулевого провода, состоящую из двух одинаковых ламп и конденсатора.
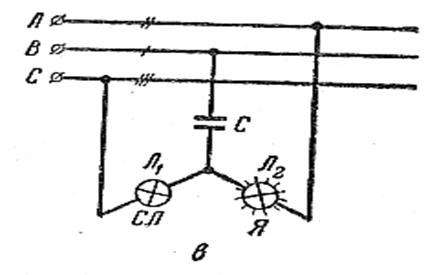
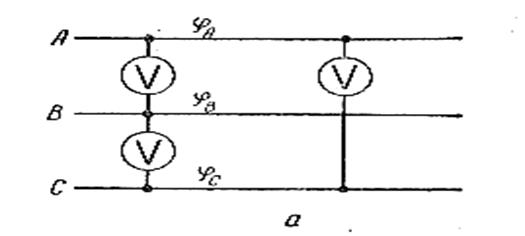
Для четкой работы фазоуказателя необходимо, чтобы R л1 = R л2 = Х С. фазоуказатель включается в сеть произвольно. Так как эта звезда несимметрична и нулевого провода нет, то нейтраль смещена и, как следствие, произошел перекос фазных напряжений. Это означает, что напряжение на лампах разное. Две одинаковые лампы, находящиеся под разными напряжениями, одинаково гореть не могут. Подсчеты и опыт показывают, что ярче горит та лампа, максимум тока в которой наступает в следующую очередь после максимума в конденсаторе. Если, например, ярче горит правая лампа, то значит порядок чередования максимумов ВАС, а последовательность в этой системе обратная (В АСВ АС). Фазоуказатель ФУ -2 представляет собой миниатюрный трехфазный двигатель, ротором которого служит алюминиевый диск, разделенный на черно-белые секторы.
В сеть фазоуказатель включается произвольно. После включения его диск начинает вращаться. Направление вращения диска указывает, в каком порядке проходят максимумы по зажимам прибора. Если диск вращается против часовой стрелки, это означает, что максимум по зажимам прибора проходит справа налево (пунктирные стрелки), следовательно, порядок чередования максимумов в сети ВСА, а последовательность прямая (ВС АВС А). Прямую последовательность прибор может показать и при вращении по часовой стрелке – все зависит от того, как включен прибор в сеть. Поэтому весьма распространенное мнение о том, что при прямой последовательности диск прибора вращается по часовой стрелке, а при обратной – против, неверно.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.114.23 (0.141 с.) |
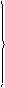 Ů А = Ė А - Ů 0;
Ů А = Ė А - Ů 0;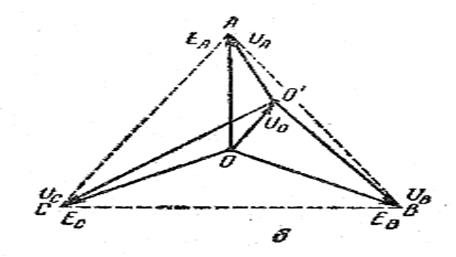
 На основании формулы,
На основании формулы,