
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула для расчета t-критерия СтьюдентаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ 1 t-критерий Стьюдента Критерий Стьюдента (t -критерий) – параметрический критерий. Назначение критерия Стьюдента – используется для проверки статистической значимости (достоверности) различий двух средних значений изучаемого психологического признака между двумя выборками (группами). Описание критерия Стьюдента Этот метод определяет влияние количественных различий средних арифметических значений и их влияние на качественные различия изучаемого психологического признака. Критерий Стьюдента позволяет прямо оценить количественные различия в средних арифметических значениях изучаемого психологического признака между двумя выборками (группами). В формулу расчета t-критерия Стьюдента включаются параметры распределения, то есть «измерение» и «разницы средних значений и их разброса». Формула для расчета t-критерия Стьюдента
где Расчет Среднее арифметическое (оценка математического ожидания) вычисляется по формуле:
где xi – каждое наблюдаемое значение психологического признака, количественно измеренного. i – индекс, указывающий на порядковый номер данного значения психологического признака; n – количество наблюдений;
М – оценка математического ожидания. Расчет ошибки средней Ошибка средней вычисляется по формуле:
где σ – стандартное отклонение или среднее квадратическое отклонение в данной выборке. Оценка σ определяется по формуле:
где xi – каждое наблюдаемое значение психологического признака;
n – количество наблюдений в выборке.
После расчета t-критерия Стьюдента необходимо это значение t сравнить с табличным значением tкр (таблица «Критические значения t-критерия Стьюдента»), вычисленным по соответствующей степени свободы n, за которую принимается сумма объемов (количество испытуемых) двух сравниваемых выборок, уменьшенная на 2 единицы. Формула для расчета степени свободы (n): n=(n1+ n2)-2 По таблице «Критические значения t-критерия Стьюдента» находим значение tкр. (по n) для уровня статистической значимости: p ≤ 0,05; p ≤ 0,01; p ≤ 0,001.
Делаем вывод.
Рассмотрим расчет критерия Стьюдента на конкретном примере. По методике Л.И. Вансовской «Техника и беглость чтения» обследовано 2 группы школьников: · n1 = 11 испытуемых · n2 = 15 испытуемых Задача: выявить статистическую значимость (достоверность) различий в средних арифметических значениях психологического признака «скорость чтения», полученных в двух группах испытуемых школьников. Условие: 2 группы школьников: · n1 = 11 испытуемых · n2 = 15 испытуемых Метод математической обработки – t-критерий Стьюдента (позволяет прямо оценить различия в средних, полученных в двух выборках). Показатели скорости чтения (слов за минуту) по каждому испытуемому, и показатели для расчета t-критерия Стьюдента представлены в табл. 1. Таблица 1 АЛГОРИТМ ЛЕКЦИЯ 2 Способ применения таблицы Номер колонки указывается в каком числе наблюдений имелся определенный признак, номер строки – какое общее число наблюдений; на пересечении колонки и строк приведен процент, который составляет число наблюдений с исследуемым признаком по отношению к общему числу наблюдений и средняя ошибка процента ( Достоверность различий:
АЛГОРИТМ Пример 1 По методике «Шкала оценки уровня реактивной и личностной тревожности» (Ч. Д. Спилбиргер, Ю. Л. Ханин) был изучен уровень личностной тревожности у стедентов-психологов двух групп: n1 =30 и n2 =30. Интерпретация результатов уровня личностной тревожности у студентов-психологов в двух группах представлена в табл. 1. Таблица 1 Уровень личностной тревожности у студентов-психологов в двух группах (n1 =30; n2 =30)
Как следует из таблицы, низкий уровень личностной тревожности одинаково часто встречается как у студентов-психологов первой, так и у второй групп (40% и 40%), умеренный – чаще в первой группе (50% и 20%) и высокий – чаще во второй группе (50% и 20%) и высокий – чаще во второй группе (40% и 10%). Для установления достоверности различий умеренного и высокого уровня тревожности в двух группах студентов-психологов необходимо выбрать метод математической обработки полученных данных.
Задача: Выявить достоверность различия в уровне исследуемого психологического признака – личностная тревожность. Условие: 2 выборки испытуемых (n1 =30 и n2 =30). 2 уровня (умеренный и высокий) личностной тревожности. Метод математической обработки – метод характеристических интервалов, т.к. позволяет определить чувствительность (частоту) различных значений уровня личностной тревожности по P Составляем таблицу для определения чувствительности (процент и его ошибка) каждой градации шкалы «умеренный и высокий уровень личностной тревожности» для каждой группы испытуемых (табл. 2). Рассчитываем t для умеренного и высокого уровня личностной тревожности по формуле:
Таблица 2
t умеренный = t умеренный = 2,63 (р <0,01) t высокий = t высокий = 2,78 (р <0,01) Эмпирические значения t умеренный и t высокий превышают табличные значения ( Таким образом, умеренный уровень личностной тревожности достоверно чаще встречается в первой группе студентов-психологов (р <0,01), а высокий – во второй (р <0,01).
Пример 2 Для проведения психокоррекционной работы выбираем вторую группу студентов-психологов, где достоверно чаще (р <0,01) выявляется высокий уровень личностной тревожности. Рассмотрим вариант 1: объект сопоставлений – одни и те же испытуемые до и после проведения психокоррекционной работы при отсутствии контрольной группы. С 12 испытуемыми экспериментальной группы была проведена психокоррекционная работа, направленная на снижение уровня личностной тревоги. После проведения психокоррекционной работы 12 испытуемых были повторно протестированы по методике «Личностная шкала проявления тревоги». Результаты полученных данных по данной группе испытуемых до и после проведения психокоррекционной работы представлены в табл. 3. Рассчитываем t для каждой шкалы по формуле:
Таблица 3 ЛЕКЦИЯ 3 Формула 1. Показатель степени (тесноты, силы) связи между двумя признаками в одной выборке (группе) испытуемых определяется по формуле линейного коэффициента корреляции:
где: x – индивидуальные показатели первого ряда признаков; ∑ x – сумма показателей первого ряда признаков; у – индивидуальные показатели второго ряда признаков; ∑ у – сумма показателей второго ряда признаков; ху – произведение показателей первого и второго ряда признаков; ∑ ху – сумма произведений показателей первого и второго ряда признаков; х2 – возведение в квадрат каждого показателя первого ряда признаков; ∑ х2 – сумма квадратов показателей первого ряда признаков; у2 – возведение в квадрат каждого показателя второго ряда признаков; ∑ у2 – сумма квадратов показателей второго ряда признаков; n – количество испытуемых.
Формула 2. Формула коэффициента линейной корреляции Пирсона:
xy – произведение величины отклонений; ∑ xy – сумма произведений величины отклонений; х2 – возведение в квадрат отклонения каждого показателя первого признака и определение суммы (∑ х2); у2 – возведение в квадрат отклонения каждого показателя первого признака и определение суммы (∑ у2). По таблице «Критические значения оценки коэффициента линейной корреляции r» находим rкр. для данного n (количество испытуемых). Сопоставляем полученное по одной из формул №1 или №2 эмпирическое значение rэмп. с критическим значением rкр. для данного n. Рассмотрим применение коэффициента линейной корреляции К. Пирсона r на конкретных примерах. Выборка из 60 испытуемых (30 пар) обследована по 2 методикам: · первая – «Оценки способов реагирования в конфликте К.Н. Томаса, тест адаптирован Н.В. Гришиной»; · вторая – «Тест-опросник удовлетворенности браком В.В. Столина, Т.Л. Романова, Г.П. Бутенко». Результаты полученных данных по каждой методике представлены в сводных таблицах. ЛЕКЦИЯ 4 Q – критерий Розенбаума Q-критерий Розенбаума относится к непараметрическим критериям. Назначение критерия. Q-критерий Розенбаума используется для оценки статической достоверности различий между двумя выборками по уровню какого-либо психологического признака, количественно (баллы, мм, см, и т.д.) измеренного. Количество испытуемых в каждой из выборок ≥ 11. Показание для применения Q-критерия Розенбаума: 1. Диапазоны разброса значений в двух выборках не должны совпадать между собой. 2. Данные психологического исследования представлены в порядковой шкале, в которой должно быть не менее трех классов, например, «низкий», «средний», «высокий» 3. Данные психологических признаков должны быть достаточно точно измерены. 4. Упорядочить значение психологического признака в обеих выборках можно как по нарастанию, так и убыванию признака. 5. Первым рядом (выборкой, группой) считать тот ряд, где значения выше, а вторым рядом – тот, где значение ниже.
Пример. У студентов экономического (n1=14) и психологического(n2=12) факультетов по методике «Шкала измерения интеллекта Д.Векслера» по суммам «сырых» оценок (отдельно вербальной и невербальной частей теста) к табличным данным были определены шкальные оценки IQ– вербального, IQ – невербального и общего IQ – показателей. Полученные индивидуального значения IQ вербального, IQ невербального и общего IQ показателей по двум выборкам представлены в соответствующих психодиагностических таблицах. Выбор метода математической обработки рассмотрим на примере психологического признака – вербальный интеллект. I. Условия: 1. Две выборки испытуемых: n1=14 студентов экономического факультета (n1>11) n2=12 студентов психологического факультета (n2 > 11) 2. Психологический показатель – IQ вербальный точно количественно измерен. Индивидуальные значения вербального интеллекта в выборках студентов экономического (n1=14) и психологического (n2=12) факультетов: Таблица 1 Индивидуальные значения вербального интеллекта в выборках студентов экономического (n1=14) и психологического (n2=12) факультетов
3. Диапазоны разброса значений вербально IQ в двух выборках не совпадают между собой: в группе студентов экономистов выше, чем в группе студентов психологов. II. Задача: Выявить различия в уровне вербального интеллекта между студентами экономического и психологического факультетов. III. Условия и задача соответствуют показанием для применения метода – Q -критерия Розенбаума.
АЛГОРИТМ подсчета критерия Q -Розенбаума на конкретном примере
Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I. Проверить выполнение условий, задач, показаний для применения критерия Q - Розенбаума | I. Условие, задача, показания позволяют использовать в качестве метода математической обработки критерий Q- Розенбаума. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| II. Построить таблицу индивидуальных значений психологического признака, количественного измеренного по каждой выборке. | II. Таблица 1 Индивидуальные значения вербального интеллекта в выборках студентов экономического (n1=14) и психологического (n2=12) факультетов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Студенты экономисты (n1=14) | Студенты психологи (n2=12) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Код имени испытуемого | Показатель вербального интеллекта | Код имени испытуемого | Показатель вербального интеллекта | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. И.А. | 132 | 1. Н.Т. | 126 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. К.А. | 134 | 2. О.В. | 127 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. К.Е. | 124 | 3. Е.В. | 132 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. П.А. | 132 | 4. Ф.О. | 120 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. С.А. | 135 | 5. И.Н. | 119 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Ст.А. | 132 | 6. И.Ч. | 126 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Т.А. | 131 | 7. И.В. | 120 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. Ф.А. | 132 | 8. К.О.
| 123 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. Ч.А. | 121 | 9. Р.Р. | 120 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. Ц.А. | 127 | 10. Р.И. | 116 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. См.А. | 136 | 11. О.К. | 123 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. К.Ан. | 129 | 12. Н.К. | 115 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. Б.Л. | 136 |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14. Ф.В. | 136 |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| III. Упорядочить значения психологического признака в каждом ряду выборок (или групп) как по нарастанию, так и убыванию признака Считать: 1 ряд - выборку (группу), где значение признака выше; 2 ряд - выборку (группу) где значения признака ниже. | Таблица 2 III. Упорядоченные ряды индивидуальных значений вербального интеллекта в двух студенческих выборках. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 1 ряд (студенты экономисты) | 2 ряд (студенты психологи) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 1. См.А. | 136 | 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 2. Б.Л. | 136 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 3. Ф.В. | 136 | S1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 4. С.А. | 135 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 5. К.А. | 134 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 6. И.Л. | 132 | 1. Е.В. | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 7. П.А. | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 8. Ст.А. | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 9. Ф.А. | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 10. Т.А. | 131 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 11. К.Ан. | 129 | 2. О.В. | 127 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 12. Ц.А. | 127 | 3. Н.Т | 126 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 13. К.Е. | 124 | 4. И.Н. | 126 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 14. Ч.И. | 121 | 5. К.О. | 123 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 6. О.К. | 123 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 7. Ф.О. | 120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 8. И.В. | 120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| S2 | 9. Р.Р. | 120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 10. И.Н. | 119 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 11. А.И. | 116 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| 12. Н.К. | 115 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| IV. Выделить самое высокое (максимальное) значения психологического показателя в 1 ряду. Обозначить – S1 | IV. Выделяем в 2 выборках 1 ряд - где показатели вербального интеллекта "выше" это группа студентов экономистов. 2-ой ряд – где показатели вербального интеллекта "ниже" - это группа студентов психологов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить количество значений второго ряда, которые меньше минимального значения первого ряда Обозначить – S2 | 4.1. Определяем количество значений первого ряда, которые больше максимального значения второго ряда (S1): S1=5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4.2. Определяем количество значений второго ряда, которые меньше минимального значения первого ряда (S2): S2=6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V. Определить эмпирическое значение Q - критерия Розенбаума по формуле: Qэмп=S1+S2 | V. Определяем эмпирическое значение Q-критерия Розенбаума Qэмп=S1+S2=5+6=11 Qэмп=11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
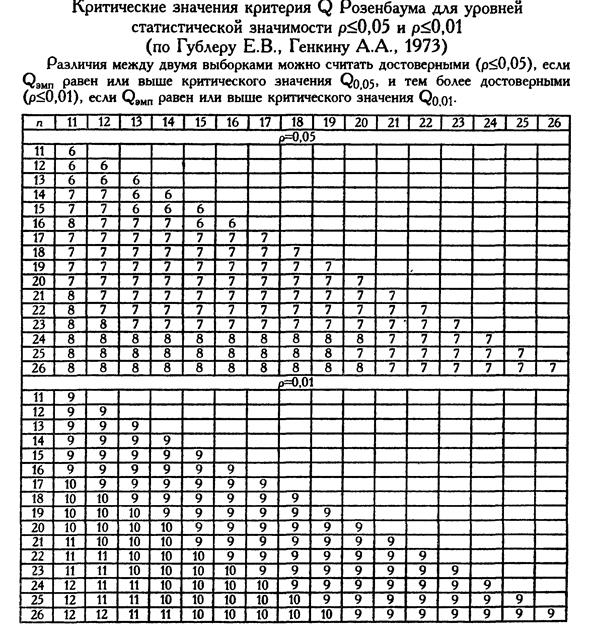
| VI. Определить критические значения Q Розенбаума для данных n1 и n2 по таблице "Критические значения критерия Q Розенбаума для уровней статической значимости p ≤ 0,05 и p ≤ 0,01 (по Гублеру Е.В., Генкину А.А., 1973), где по горизонтали таблицы расположены показатели меньшего количества испытуемых, а по вертикали – большего количества испытуемых. На пересечении этих показателей определяются достоверность значений для p ≤ 0,05 и p ≤ 0,01 | VI. Определяем критическое значение критерия Q для n1 = 14 и n2 = 12.
Qэмп(11)>Qкр (7 и 9), (p<0,01) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| VII. Различия между выборками можно считать статически достоверными (p≤0,05; p≤0,01), если Qэмп равен или выше Qкр. Значения: 1. Qэмп ≥ Qкр. 0,05; Qкр. 0,01 2. Если Qэмп ≥ Qкр. 0,05; 0,01 – H1 - принимается, а Н0 – отвергается. | VII. Студенты-экономисты по уровню вербального интеллекта статистически достоверно превосходят студентов психологов (p<0,01). Принимается Н1, Н0 – отвергается | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VIII. Графическое представление критерия
Q-Розенбаума.
8.1 Построить ось значимости Если Qэмп окажется на границе зоны незначимости, то различия достоверны при p ≤ 0,05. Если Qэмп окажется между двумя критическими значениями, тоQэмп≥Qкр различия достоверны (р<0,05). Если Qэмп оказывается на границе зоны значимости, то различия достоверны при p≤0,01. Если Qэмп попадает в зону значимости, то p<0,01
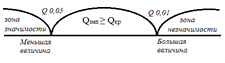 
| VIII. Построим "ось значимости"
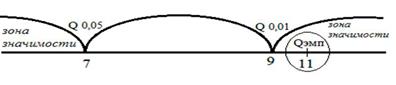
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 3. 1
ЛЕКЦИЯ 5
U – критерии Манна-Уитни
[13,49-56]
U -критерий Манна-Уитни относится к непараметрическим критериям с использованием ранжирования.
Назначение критерия
Критерий Манна-Уитни предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественного измеренного.
Показания для применения U -критерия Манна-Уитни:
1. В каждой выборке должно быть не менее 3 наблюдений: n1,n2 ≥ 3
2. Если в одной выборке 2 наблюдения, то во второй их должно быть не менее 5.
3. В каждой выборке должно быть не более 60 наблюдений: n1, n2< 60. Однако уже при n1, n2 ≥ 20 ранжирование становиться достаточно трудоемким.
4. Первым рядом (выборкой, группой) считается тот ряд значений, в котором значения, по предварительной оценке, выше, а вторым рядом – тот, где они предположительно ниже.
5. Знать правила ранжирования.
Правила ранжирования
1. Меньшему значению начисляется меньший ранг.
Наименьшему значению начисляется ранг 1.
Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Например, если n=7, то наибольшее значение получит ранг 7, за возможным исключением для тех случаев, которые предусмотрены правилом 2.
2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из этих рангов, которые они получили бы, если бы не были равны.
Например, 3 наименьших значение равны 10 секундам.
Если бы мы измеряли время более точно, то эти значения могли бы различаться и составляли бы, скажем, 10,2; 10,4; 10,7 сек. В этом случае они получили бы ранги, соответственно, 1, 2 и 3. Но поскольку полученные нами значения равны, каждое из них получает средний ранг:
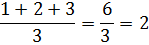
Допустим, следующие 2 значения равны 12 сек. Они должны были бы получить ранги 4 и 5, но, поскольку они равны, то получают средний ранг:
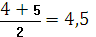 и т.д.
и т.д.
3. Общая сумма рангов должна совпадать с расчетной. Которая определяется по формуле:
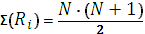
где N – общее количество ранжируемых наблюдений (значений).
Несовпадение реальной и расчетной суммы ранга будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжать работу, необходимо найти ошибку и устранить ее.
Рассмотрим применение U-критерия Манна-Уитни на примере опросника «Шкала депрессий» (Г.А.Балашова)
Цель: выявить депрессивные состояния и состояния близкие к депрессии.
По данному опроснику проведено тестирование 2 выборок (групп) испытуемых:
· 1-я выборка – n1=25 испытуемых (экспериментальная)
· 2-я выборка – n2=20 испытуемых (контрольная)
Результаты тестирования по данному опроснику каждой выборки предоставлены в табл. 2.
Таблица 2
АЛГОРИТМ
критерия U – Манна-Уитни на конкретном примере
| Подсчет критерия U Манна-Уитни | |||||||
Пример
I. Из сводной таблицы каждой выборки выбрать индивидуальные показатели по исследуемому психологическому признаку и построить таблицу.
I.
Таблица 1
Индивидуальные значения «истинного депрессивного состояния» в баллах
Первая выборка
(n1 = 12)
Вторая выборка
(n2 = 3)
Показатель - баллы
Показатель - баллы
74 78 72 75 77 80 79 76 74 72 73 78
71 72 72
II. Проранжировать полученные индивидуальные значения психологического показателя, исходя из правил ранжирования. Провести подсчет ранговых сумм по выборкам
II.
Таблица 2
Подсчет ранговых сумм психологического признака "истинное депрессивное состояние" по экспериментальной и контрольной группам
Первая (n1=12)
Вторая (n2=3)
Показатель, в баллах
Ранг
Показатель, в баллах
80 79 78 78 77 76 75 74 74 73 72 72
15
14
12,5
12,5
11
10
9
7,5
7,5
6
3,5
3,5
72
72
71
Суммы рангов
112
Суммы рангов
III
3.1 Общая сумма рангов 112+8 = 120
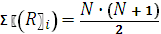 где N – общее количество ранжируемых наблюдений (значений)
где N – общее количество ранжируемых наблюдений (значений)
3.2 Расчетная сумма рангов:
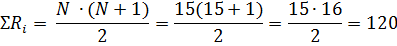
3.3. Равенство реальной и расчетной сумм соблюдено. По уровню «истинное депрессивное состояние» более высоким рядом оказывается первая выборка испытуемых.
3.4. На эту выборку приходится большая ранговая сумма: 112
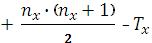 где – n1- количество испытуемых в выборке 1;
n2 - количество испытуемых в выборке 2;
Tx - большая из двух ранговых сумм;
nx- количество испытуемых в группе с большей суммой рангов.
где – n1- количество испытуемых в выборке 1;
n2 - количество испытуемых в выборке 2;
Tx - большая из двух ранговых сумм;
nx- количество испытуемых в группе с большей суммой рангов.
IV.
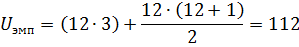
(36+78) - 112=2
Uэмп=2
V.
n1=3 n2=12
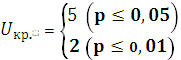
Uэмп = Uкр: 2 = 2 (p<0,01)
Таким образом, выявлена статистическая достоверность психологического признака "истинное депрессивное состояние" в первой выборке испытуемых по сравнению со второй (p<0,01) H1 принимается, H0 – отвергается
VI. Графическое представление U критерия Манна-Уитни
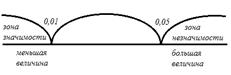 Uэмп≤ Uкр
Uэмп≤ Uкр
6.1. Построим ось значимости
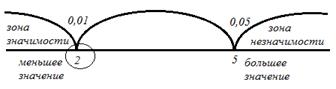
Uэм = Uкр: 2 = 2(p<0,01)
ЛЕКЦИЯ 6
φ* – критерий (угловое преобразование Фишера)
Критерии φ* Фишера (угловое преобразование Фишера) относится к числу многофункциональных критериев. Этот критерий может быть использован по отношению к самым разнообразным данным, выборкам и задачам. Данные могут быть представлены в любой шкале, начиная от наминативной (шкалы наименований).
Выборки могут быть как независимыми, так и «связанными», то есть можно сравнивать и разные выборки испытуемых, и показатели одной и той же выборки, измеренные в разных условиях.
Суть критерии φ* состоит в определении процентной доли (например, 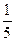 =20%) исследуемого психологического признака, в котором зафиксирован интересующий исследователя эффект (есть «эффект»).
=20%) исследуемого психологического признака, в котором зафиксирован интересующий исследователя эффект (есть «эффект»).
Путем сведения любых данных к альтернативной шкале «Есть эффект – нет эффекта» критерий φ* позволяет разрешить все три задачи сопоставлений: сравнение «уровней», оценки «сдвигов» и сравнения распределений.
Критерий φ* Фишера, позволяет оценить достоверность различий по частоте (процентной доле) встречаемости эффекта психологического признака путем сопоставления (сравнения) двух выборок.
Ограничения критерия φ*
1. Ни одна из сопоставленных долей не должна быть равной нулю.
2. Нижний предел в критерии φ* – 2 наблюдения в одной из выборок, однако должны соблюдаться следующие соотношения в численности двух выборок:
· Если в одной выборке всего 2 наблюдения, то во второй должны быть не менее 30: n1=2 → n2≥ 30
· Если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7: n1=3 → n2≥ 7
· если в одной из выборок 4 наблюдения, то во второй должно быть не менее 5: n1=4 → n2≥ 5
· при n1,n2≥ 5 возможны любые сопоставления
3. Верхний предел в критериях φ* отсутствует – выб
|
| Поделиться: |

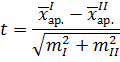
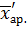 и
и 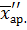 – средние арифметические значения изучаемого психологического признака в каждой выборке.
– средние арифметические значения изучаемого психологического признака в каждой выборке.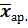
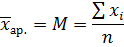
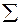 – знак суммирования.
– знак суммирования.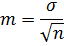
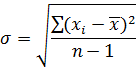
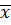 – среднее арифметическое значение признака;
– среднее арифметическое значение признака;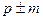 ).
).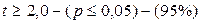
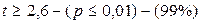
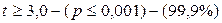
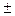 m.
m.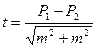
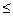 )
)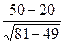 =
= 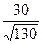 =
= 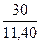 = 2,63
= 2,63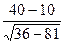 =
= 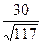 =
= 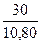 = 2,78
= 2,78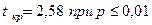 ), значит принимается гипотеза Н0.
), значит принимается гипотеза Н0.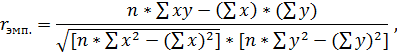
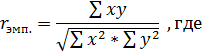
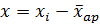 x – отклонение каждого показателя первого признака от средней арифметической.
xi – каждое наблюдаемое значение первого признака.
Расчет
x – отклонение каждого показателя первого признака от средней арифметической.
xi – каждое наблюдаемое значение первого признака.
Расчет 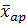 (Мх) – средней арифметической по формуле:
(Мх) – средней арифметической по формуле:
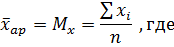 х – каждое наблюдаемое значение первого признака;
i – индекс, указывающий на его порядковый номер;
n – количество наблюдений;
∑ – знак суммирования.
х – каждое наблюдаемое значение первого признака;
i – индекс, указывающий на его порядковый номер;
n – количество наблюдений;
∑ – знак суммирования.
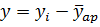 y – отклонение каждого показателя второго признака от средней арифметической.
yi – каждое наблюдаемое значение второго признака.
Расчет
y – отклонение каждого показателя второго признака от средней арифметической.
yi – каждое наблюдаемое значение второго признака.
Расчет 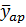 (М y) – средней арифметической по формуле:
(М y) – средней арифметической по формуле:
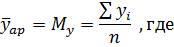 y – каждое наблюдаемое значение второго признака;
i – индекс, указывающий на его порядковый номер;
n – количество наблюдений;
∑ – знак суммирования.
y – каждое наблюдаемое значение второго признака;
i – индекс, указывающий на его порядковый номер;
n – количество наблюдений;
∑ – знак суммирования.
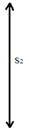
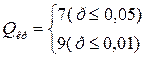
 Qэмп находится в зоне значимости (p<0,01) Qэмп(11)>Qкр(9)
Qэмп находится в зоне значимости (p<0,01) Qэмп(11)>Qкр(9)


