Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эмпирическое распределение словесных формулировок, отражающих мотивы «надежды на успех» и «боязнь неудачи».Содержание книги
Поиск на нашем сайте
Вопрос 1: Можно ли утверждать, что разные картины методики Хекгаузена обладают разной побудительной силой в отношении мотивов: · «надежды на успех»; · «боязнь неудачи». Для ответа на данный вопрос необходимо принять решение о выборе метода математической обработки. Так как данные уже получены и представлены в таблице, чтобы ответить на данный вопрос, необходимо принять решение о задаче, условии решения задачи и выборе критерия. Задача: Выявить различия в распределении признака: · «надежда на успех»; · «боязнь неудачи». Условие решения задачи: Сопоставить эмпирическое распределение реакции признака «надежда на успех» и реакции признака «боязнь неудачи» с теоретическим (равномерным распределением). Это позволит проверить, равномерно ли распределяются реакции «надежды на успех» по шести картинам и равномерно ли распределяются реакции «боязнь неудачи» по шести картинам.
Метод математической обработки: c2 – критерий Пирсона Количество наблюдений достаточно велико, поэтому можно было бы использовать критерий Колмогорова-Смирнова. Однако в исследовании картины предъявлялись разным испытуемым в разной последовательности, то есть отсутствует однонаправленное изменение признака в какую-либо сторону: все разряды (картины) следуют друг за другом в случайном порядке. Поэтому методом выбора математической обработки является критерий c2, а не критерий λ. Расчет критерия c2 при сопоставлении распределения реакций «надежды на успех» по 6 картинам с равномерным распределением представлен в табл. 3.18. Таблица 12 Расчет критерия c2 при сопоставлении распределения реакций «надежды на успех» по 6 картинам, с равномерным распределением.
АЛГОРИТМ расчета критерия c2
Пример 2
Расчет критерия c2 при сопоставлении распределения реакций «боязнь неудачи» по 6 картинам с равномерным распределением представлен в табл. 13. Таблица 13 Расчет критерия c2 при сопоставлении распределения реакций «боязнь неудачи» по 6 картинам с равномерным распределением.
Суммы | 516 | 516 | 0 | 19442 | 226,06 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Определяем количество степеней свободы n по формуле:
n = k – 1
n = 6 – 1 = 5
Поправка на «непереносимость» не нужна. Производить расчет критерия c2 необходимо по общему алгоритму.
2. Рассчитываем теоретические частоты для равномерного распределения по формуле:
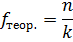
где n – количество наблюдений – это сумма эмпирических частот реакций «боязнь неудачи», n = 516.
k – количество разрядов – это число стимульных картин, k = 6.
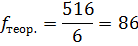
3. Подсчитываем разности между эмпирической и теоретической частотой по каждому разряду (строке) и записываем в столбец 4.
4. Возводим в квадрат полученные разности и заносим их в столбец 5.
5. Разделить полученные квадраты разностей на теоретическую частоту и занести в столбец 6.
6. Определяем 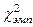 по сумме значений столбца 6.
по сумме значений столбца 6.
7. По таблице «Критические значения критерия c2» определяем критические значения c2 при n = 5.
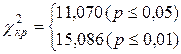
8. 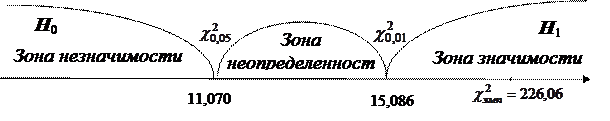 Построим «ось значимости»
Построим «ось значимости»
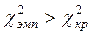
Вывод: распределение проявлений «боязнь неудачи» по шести стимульным картинам достоверно отличается от равномерного распределения (р < 0,01).
Пример 3
Результаты, полученные в эксперименте по заучуванню ряда из 20 чисел для 100 испытуемых предоставлены в таблице. С помощью критерия Пирсона (c2 – критерия) проверить гипотезу о нормальности распределения случайной величины Х – количества заученных чисел.
Таблица 14
|
| Поделиться: |

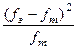
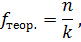 где n – количество наблюдений (сумма эмпирических частот психологического признака).
k – количество разрядов.
(столбец 3)
где n – количество наблюдений (сумма эмпирических частот психологического признака).
k – количество разрядов.
(столбец 3)
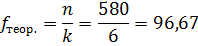 (столбец 3)
(столбец 3)
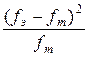
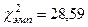
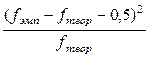 – столбец 6
Для данного числа степеней свободы n по таблице «Критические значения критерия c2 для уровней статистической значимости р ≤ 0,05 и р ≤ 0,01 при разном числе степеней свободы V» определяем критическое значение
– столбец 6
Для данного числа степеней свободы n по таблице «Критические значения критерия c2 для уровней статистической значимости р ≤ 0,05 и р ≤ 0,01 при разном числе степеней свободы V» определяем критическое значение 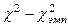 .
.
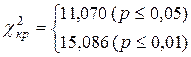
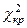 , то расхождения между распределениями статистически недостоверны.
Если
, то расхождения между распределениями статистически недостоверны.
Если 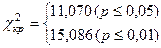
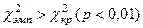
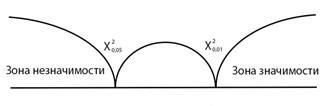 IX. Построить «ось значимости»
IX. Построить «ось значимости»