
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задачи ЛПРСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
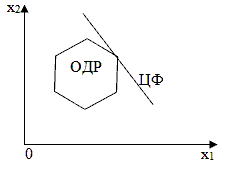
Графические методы решения имеет ограниченный круг использования. Число неизвестных переменных должно быть не более трех. Только в этом случае решение задачи можно наглядно отобразить на бумаге или экране монитора. При графическом представлении двухмерной задачи ЛПР область допустимых решений называют многоугольником допустимых решений. Если задача трехмерная, то область допустимых решений выглядит в виде объемной трехмерной фигурой, ограниченной с разных сторон плоскостями. Типичный случай графического решения двухмерной задачи выглядит следующим образом:
График целевой функции имеет одну единственную точку прикосновения с ОДР, причем в этой точке ЦФ имеет оптимальное значение. Оптимальное решение задачи ЛПР всегда достигается в одной из вершин многоугольника допустимых решений. Именно к такой ситуации следует стремиться при графическом решении задачи ЛПР. В показанном на рисунке случае число ограничений равно 6. Стороны изображенного многоугольника описываются прямыми, уравнения которых берутся из ограничений (2). При построении многоугольника допустимых решений знаки неравенств в ограничениях заменяются знаками равенств. Таким образом, точки внутри многоугольника допустимых решений удовлетворяют сразу всем неравенствам. Построение многоугольника допустимых решений и графика целевой функции Пусть нужно максимизировать ЦФ вида z=d1x1+d2x2 при имеющихся ограничениях: a11x1+a12x2<=b1 a21x1+a22x2<=b2… am1x1+am2x2<=bm x1>=0, x2>=0 Для построения многоугольника допустимых решений вначале строится прямая a11x1+a12x2=b1. При построении целесообразно расположить точки прямой на осях системы координат. Взяв x1=0, x2=b1/a12, при x2=0, x1=b1/a11.
A
0 B x1
Аналогично строятся остальные прямые и выбираются полуплоскости, соответствующие указанному ограничению. В результате получается многоугольник допустимых решений, представляющий собой общую часть всех полуплоскостей, которая определяется с помощью ограничений. После построения многоугольника допустимых решений нужно на нем найти, где ЦФ принимает максимальное значение. На график с изображением многоугольника допустимых решений наносится прямая линия, которая описывает ЦФ в соответствии с формулой (1).
x2
ЦФ
0 x1
Первоначально прямую линию графика ЦФ проводят так, чтобы она пересекала многоугольник допустимых решений. Затем эту прямую перемещают в сторону увеличения целевой функции до тех пор, пока прямая линия имеет хотя бы одну точку с ОДР. Для ЦФ вида z= d1 x1+ d2 x2 прямую линию следует перемещать параллельно самой себе в направлении вектора d с координатами (d1; d2). При минимизации ЦФ прямую линию смещают в направлении вектора (- d1;- d2). При графическом решении задач ЛПР: 1. Строятся прямые линии на основании ограничений, в которых знаки неравенства заменяются знаками равенств. 2. Находятся полуплоскости, которые определяются каждым из имеющихся ограничений. В результате получается многоугольник допустимых решений. 3. На основании уравнения, которое описывает ЦФ, строится вектор-градиент d с координатами (d1;d2), определяющие вектор возрастания ЦФ. 4. Выбрав некоторое постоянное значение h, строится график ЦФ d1x1+d2x2=h, который должен пересекать многоугольник допустимых решений. График ЦФ будет обязательно перпендикулярен вектору d. 5. Увеличивается значение h до тех пор, пока график ЦФ имеет хотя бы одну общую точку с ОДР. При увеличении h график ЦФ смещается параллельно самому себе в направлении возрастания вектора d. 6. Определяет точка или отрезок, где ЦФ принимает максимальное значение в этой точке или на этом отрезке переменные xi имеет оптимальное значение. Пример. Для производства двух видов изделий А и В предприятие использует три вида сырья. Норма расхода сырья каждого вида на изготовление единицы продукции данного вида приведено в таблице. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Решение. Предположим, что предприятие изготовит
Общая прибыль от реализации Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение. Решим сформулированную задачу геометрическим способом. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдём соответствующие прямые:
Эти прямые изображены на рисунке. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли её координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость. Найдем, например, полуплоскость, определяемую неравенством 12
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи. Как видно из рисунка, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию не отрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение. Чтобы найти указанную точку, построим вектор Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то её координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют план производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб. Перемещая построенную прямую Найдем координаты точки В, как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых: Решив эту систему уравнений, получим
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.245.152 (0.007 с.) |
|||||||||||||||||||||||||

 x2
x2



 изделий вида А и
изделий вида А и 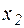 изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьём каждого вида, и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:
изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьём каждого вида, и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства: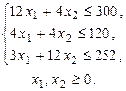
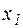 изделий вида А и
изделий вида А и 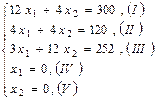
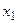 +4
+4 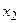 <300. Для этого, построив прямую 12
<300. Для этого, построив прямую 12 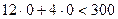 , значит, полуплоскость, которой принадлежит точка O(0;0), определится неравенством
, значит, полуплоскость, которой принадлежит точка O(0;0), определится неравенством 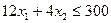 . Это и показано стрелками на рисунке.
. Это и показано стрелками на рисунке.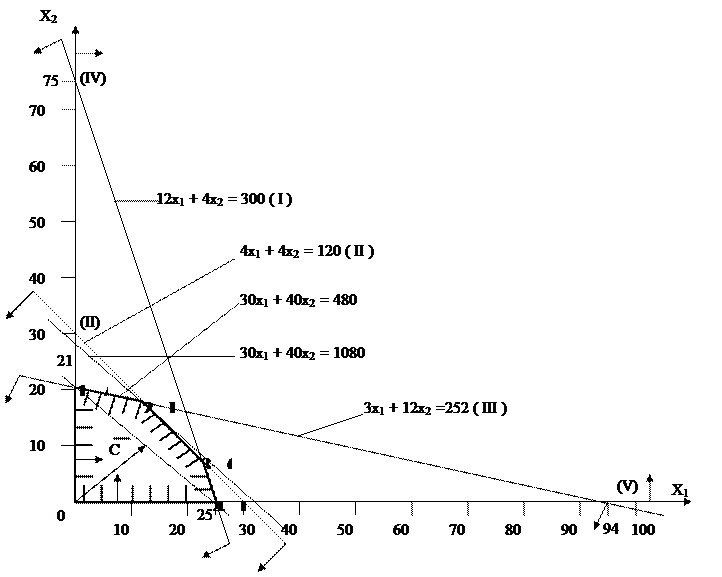
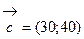 и прямую
и прямую 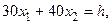 где h – некоторая постоянная такая, что прямая
где h – некоторая постоянная такая, что прямая 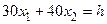 имеет общие точки с многоугольником решений. Положим, например, h=480 и построим прямую
имеет общие точки с многоугольником решений. Положим, например, h=480 и построим прямую 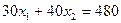 (см. рис.). Точки пересечения с осями
(см. рис.). Точки пересечения с осями 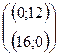 .
.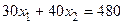 в направлении вектора
в направлении вектора 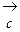 , видим, что последней общей точкой её с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.
, видим, что последней общей точкой её с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.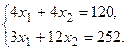
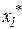 =12,
=12, 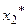 =18. Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную
=18. Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную 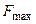 =
= 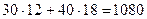 руб.
руб.


