
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. 2 нелинейное программированиеСодержание книги
Поиск на нашем сайте
Как известно, общая задача математического программирования формулируется следующим образом: найти вектор
Если Задачи нелинейного программирования делятся на следующие типы: 1. Когда нелинейная ЦФ и линейная – система ограничений; 2. Линейная ЦФ и нелинейные ограничения; 3. Нелинейная ЦФ и система нелинейных ограничений. Особенностью поиска экстремума в задачах нелинейного программирования является то, что решение может находиться как в вершинах ОДР, так на ребрах и внутри ОДР. Может быть несколько локальных экстремумов внутри или на границе ОДР. Как правило, ограничиваются поиском первого локального экстремума. Оптимальное решение – значение вектора входных параметров x* = x1,x2,xn и соответствующее ему значение ЦФ. L(x*) – достигающая максимального значения. Локальным оптимальным решением называется значение ЦФ L(x*) экстремальная в некоторой дельта окрестности. Глобальным оптимальным решением является экстремальное значение ЦФ во всей ОДР. Допустимость – любой вектор x входных параметров, удовлетворяющий условиям ограничений называется допустимым вектором или допустимой точкой. Множество допустимых точек задает ОДР. Если наилучшее решение, но не экстремальное находится на границе ОДР, то такое решение называется условно оптимальным. Ограничение в виде неравенства обеспечивает нахождение вектора входных параметров внутри ОДР. Ограничение в виде равенства обеспечивает нахождения вектора входных параметров на пересечении гиперповерхностей. Допустимые или внутренние точки могут находиться внутри ОДР, внутри ОДР на пересечение гиперплоскостей или на границе ОДР. Точки, лежащие за пределами ОДР, называются недопустимыми или внешними. Градиент. Линией уровня называется множество точек, на которых ЦФ имеет постоянные значения. Если в какой-либо точке функция непрерывна и дифференцируема, то в этой точке существует градиент ЦФ. Градиент указывает направление наискорейшего возрастания функции, антиградиент – противоположные направления – убывания. Градиент определяется как вектор-столбец первых частных производных целевой функции L(x) по переменной x. Аппроксимация функции. При решении задач НПР наиболее трудоемкой является вычисление первых и вторых производных. Поэтому в некоторых методах используют линейную и квадратичную аппроксимацию. Линейная аппроксимация выполняется с помощью усеченного ряда Тейлора в окрестности точки x. Квадратичная получается из разложения в ряд Тейлора путем отбрасывания членов третьего и старшего порядков. Необходимые и достаточные условия оптимальности решения Полностью критерии оптимальности для задач НЛП не разработаны. Он формулируется для некоторого круга задач. Необходимыми условиями нахождения локального экстремума функции является: 1. ЦФ дифференцируема в точке x*; 2. Если первая производная ЦФ равна 0 в точке x*, то эта точка является стационарной. Достаточными условиями существования локального экстремума являются названные необходимые условия и следующие: вторые производные ЦФ должны быть положительно определены. В случае поиска максимального значения вторые производные должны быть отрицательно определены.
|
||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

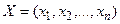 , удовлетворяющий системе ограничений:
, удовлетворяющий системе ограничений: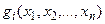 £ bi, i =1,…, m, (система иногда представляется через знак "=", но равенства всегда можно переделать в неравенства) и доставляющий экстремум функции
£ bi, i =1,…, m, (система иногда представляется через знак "=", но равенства всегда можно переделать в неравенства) и доставляющий экстремум функции  . При этом предполагается, что известны функции
. При этом предполагается, что известны функции 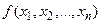 . Обычно на некоторые переменные из набора
. Обычно на некоторые переменные из набора 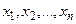 накладывается условие неотрицательности.
накладывается условие неотрицательности. и
и 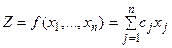 , где
, где 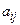 и
и 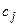 - известные константы, то при условии неотрицательности решения получаем задачу линейного программирования. Любую другую задачу математического программирования, не удовлетворяющую таким условиям, будем считать нелинейной.
- известные константы, то при условии неотрицательности решения получаем задачу линейного программирования. Любую другую задачу математического программирования, не удовлетворяющую таким условиям, будем считать нелинейной.


