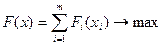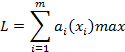Тема 2.3 Динамическое программирование

 

Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги). Все шаги могут быть уникальными или одинаковыми и чередоваться друг с другом. Некоторые задачи оптимизации легко разделяются на шаги естественным способом, а для других вводится искусственное разделение на шаги.

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.

Экономический процесс является управляемым, если можно влиять на ход его развития.

Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.

Операция– управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.

Решение на каждом шаге называется «шаговым управлением». Совокупность всех шаговых управлений представляет собой управление операцией в целом.

Примерами задач, решаемых методом динамического программирования, могут быть: распределение ресурсов (финансовых, сырьевых, материальных и т.д.) между предприятиями, замена или ремонт промышленного оборудования, прокладка коммуникаций (трубопроводов, дорог и т.д.) и пр. В этих задачах, как правило, в качестве шагов выступают отрезки времени, которые явно задаются в условии задачи.

 

Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:

где F – выигрыш за операцию;

F_i(x_i) – выигрыш на i-м шаге;

х – управление операцией в целом;

х_i – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х₁, х₂, … х _m) могут стать числами, векторами, функциями.

То управление (х *), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*₁, х*₂, … х*_m

F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.

Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.

Нахождение кратчайшего пути

Выбор оптимального решения на конкретном шаге не дает гарантии получения оптимального решения всей задачи. Поэтому для получения оптимального решения в задаче иногда приходится выбирать не лучшее решение на конкретном шаге. Планирование многошаговой задачи сводится к выбору такого решения на каждом шаге, которое учитывает последствие на следующих шагах. На текущем шаге выбирается не лучшее решение, а то, которое предполагает максимальную сумму выигрыша от всех оставшихся шагов. Поэтому выполнять вычисления в задачах ДП удобнее от конца к началу. Выполняя вычисление по последнему шагу, делается ряд предположений, как закончился предыдущий шаг и для каждого предположения найти условно оптимальное решение до первого шага. Т.о. будут найдены условно-оптимальные решения на каждом шаге. Далее выполняется переход от условно-оптимального к безусловно-оптимальному решению. Вычисления идут от первого шага к последнему, используя полученные условно-оптимальные решения.

Распределение ресурсов

Общий подход к решению задач распределения ресурсов тот же, но имеют некоторые особенности. Распределить некоторый ресурс, например, финансы в объеме S между предприятиями P₁, P₂, P_n. Вложение в каждое предприятие должно приносить дополнительную прибыль. Чем больше сумма финансовых вложений в предприятие, тем больше дополнительный доход. Но может быть так, что начиная с какого-то момента, дополнительная прибыль не увеличивается, т. е. предприятие не может освоить выделенные ресурсы.

Задача распределения ресурсов стоит так: как распределить выделенные ресурсы между предприятиями, чтобы суммарный доход от всех предприятий был максимальным. Распределяемые ресурсы выделяются порциями, распределенные во времени. Перед каждым шагом имеется некоторая сумма S еще не распределенных ресурсов. На каждом шаге предприятиям назначаются ресурсы x₁, x₂, x_n. Требуется найти оптимальное сочетание x₁, x₂, x_n, при котором совокупный доход максимален.

Оптимизацию начинаем с последнего шага m. На этом шаге остаток ресурсов S. Их нужно назначить последнему предприятию Pn. Оптимальное решение будет выглядит x_n(S)=S. Условно-оптимальный доход составит L_m(S)=α_m(S). На предпоследнем шаге n-1 запас ресурсов S, а условно-оптимальный доход на двух последних шагах, L_n-1(S) Если на предпоследнем шаге будут выделены ресурсы x, то на последнем шаге ресурсов останется S-x и условно—оптимальный жоход на двух последних шагах составит Ln-1(S)=αn-1(S)+Ln(S-x) и нужно найти такой x, чтобы доход был максимальным.

Дойдя до первого шага будем иметь начальное значение ресурсов Q, поэтому условно-оптимальный доход составит: L=max{α_1(x)+L_2(Q-x)}. Далее выполнить обратное вычисление и уточнить распределение ресурсов.