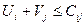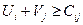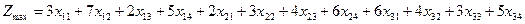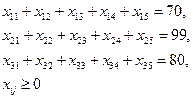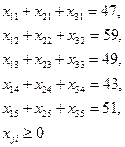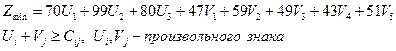Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Основы моделированияСтр 1 из 13Следующая ⇒
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Поволжский государственный университет телекоммуникаций и информатики»
КОЛЛЕДЖ СВЯЗИ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ Конспект лекций
Самара, 2014 СОДЕРЖАНИЕ Раздел 1. ОСНОВЫ МОДЕЛИРОВАНИЯ.. 3 Раздел 2. ДЕТЕРМИНИРОВАННЫЕ ЗАДАЧИ.. 9 Тема 2.1 Линейное программирование. 9 Графический метод решения задачи ЛПР. 12 Двойственность в задачах линейного программирования. 17 Симплексный метод решения задач линейного программирования. 21 Транспортная задача. 26 Тема 2.2 Нелинейное программирование. 34 Тема 2.3 Динамическое программирование. 43 Раздел 3. Задачи в условиях неопределенности. 50 Тема 3.1 Системы массового обслуживания. 50 Марковский случайный процесс. 50 Схема гибели и размножения. 52 Моделирование систем массового обслуживания. 53 ЛИТЕРАТУРА.. 59
Материальные модели Модели этой группы реализованы в виде реальных физических объектов – макетов. Модели связаны с оригиналом различными характеристиками: геометрическими, физическими и т. д. Изучение оригинала производится путем воздействия на макет и обработкой реакций макета на суммарное воздействие. Такой метод исследования называется экспериментальным. Материальные модели подразделяются на макеты подобия (физические модели) и заменяющие макеты (аналоговые модели). Физическое моделирование основано на устройствах, математическое описание процессов функционирования которых, подобно описанию процессов в реальной системе. Взаимный перевод параметров от оригинала к модели и обратно производится с помощью теории подобия. Модели могут быть представлены в реальном, уменьшенном или увеличенном масштабе времени. Физические модели часто имеют ту же природу, что и оригинал (например, продувки в аэродинамических трубах моделей самолетов, скоростных поездов, автомашин). Перед реконструкцией дорог, когда требуется сужать проезжую часть, целесообразно предварительно промоделировать такое сужение, оценить характеристики трассы, на основе чего принять меры, позволяющие существенно не снизить её пропускную способность.
Аналоговыми моделями называют системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается, например, дифференциальными или алгебраическими уравнениями.
Идеальные модели В этом случае создается либо мысленный образ объекта или явления в памяти человека или ПК, либо абстрактная математическая модель. Такая модель носит теоретический характер. Идеальные модели делятся на: 1. Сущностные (интерактивные), создаваемые в памяти человека или компьютера, для создания которых, как правило, не требуется строгих уравнений. Законы функционирования таких моделей строятся на наблюдениях за оригиналом. 2. Символьные (знаковые) построены на наборе символов: алфавит, пиктограмма, технические символы и т.д. Символьные модели могут выступать в виде графиков, чертежей, рисунков, текстов, формул. Одним из видов символьных моделей являются математические модели. Математическое моделирование основано на аналогии данной реальной системе некоторых математических уравнений, описывающих процессы в модели, исследование которых позволяет получать характеристики функционирования оригинала. Математические модели: 1. Дескриптивные; 2. Оптимизационные; 3. Игровые; 4. Имитационные; 5. Многокритериальные; 6. Модели прогнозирования. Дескриптивные модели – объект, явление или процесс описываются математическими уравнениями. Наиболее часто используются в механике, физике, химии и т. д. и описывают протекающие процессы без вмешательства в ход событий. Оптимизационные модели – предназначены для управления объектом, явлением или процессом. Строятся с целью получения наилучших результатов при изменении управляющих факторов.
Игровые модели – применяются для управления процессами, которые противодействуют исследователю. Имитационные модели – используются для моделирования сложных технических систем или общественных процессов, когда не ясно, какую цель нужно достигнуть. Многокритериальные модели – применяются для нахождения наилучшего решения по нескольким целевым функциям. Модели прогнозирования – позволяют создать прогноз о поведении объекта или системы. По степени точности математические модели делятся на: · Аналитические модели – используются для описания простых процессов, явлений и объектов и учитывают небольшое количество факторов. Такие модели грубы, но лучше приспособлены к отысканию оптимального решения и имеют наглядные и простые решения;
· Статистические модели – строятся на основе данных за поведением реального процесса явления или объекта. Исходные данные носят случайный характер. Каждое воздействие на такую модель называется реализацией. После выполнения большого количества реализаций, полученные результаты обрабатываются специальными методами и в результате получают усредненные характеристики процесса, явления или объекта. Такие модели позволяют учитывать больше факторов, но они более громоздки и полученные результаты носят усредненный характер, плохо воспринимаются и плохо приспособлены к поиску оптимального решения.
В своей основе каждая математическая модель имеет целевую функцию, которая описывает функционирование реального объекта, процесса или явления. В зависимости от исследуемого объекта целевая функция может быть представлена одной функциональной зависимостью, системой уравнений, набором статистических данных и т. д. При работе с целевой функцией исследователь воздействует на нее через набор входных параметров. Реакция математической модели (целевой функции) на набор входных воздействий называется решением – вектор выходных параметров. Т. к. на математическую модель можно подавать множество наборов входных параметров, то в результате будет множество решений. Лучшее решение по заранее обговоренным признакам называется оптимальным. Кроме набора входных параметров и значения оптимального решения исследователю приходится иметь дело с ограничениями на значения входных параметров. Они могут быть заданы в виде равенств или неравенств и описаны как линейными, так и нелинейными зависимостями. По способу реализации математические модели делятся на: 1. Линейное программирование. Математическая модель целиком описывается уравнениями первого порядка. Включает в себя следующие методы решения: симплексный, графический, транспортная задача, целочисленное программирование. 2. Нелинейное программирование. Целевая функция и ограничение, составляющие математическую модель содержит хотя бы одно нелинейное уравнение. Методы решения: графический, методы прямого поиска, регулярного симплекса, деформированного многогранника, градиентный. 3. Динамическое программирование. Ориентировано на решение задач прокладки магистралей кратчайшим путем и перераспределение различных видов ресурсов.
4. Сетевое планирование. Решает проблему построения графика выполнения работ, распределение производственных, финансовых и трудовых ресурсов. 5. Принятие решений и элементов планирования. В этом случае в качестве целевой функции выступает набор статистических данных или некоторые данные прогнозы. Решением задачи являются рекомендации о способах поведения. Решение носит рекомендательный характер. Выбор стратегии остается за человеком, принимающим решение. Для принятия решения разработаны следующие теории: теория игр и система массового обслуживания.
Задача производства К группе задач о производстве относят задачи, целью которых является подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья.
Пример. Предприятие по производству мебели производит мебель трёх типов: наборы пристенной мебели (далее «стенки»), шкафы для одежды (далее «шкафы») и кухонные гарнитуры (далее «гарнитуры»). Для их производства в основном используются три типа сырья: древесина, стекло, зеркала. Удельные коэффициенты расхода сырья, а также трудозатраты на единицу каждого типа мебели приведены в таблице.
Запасы сырья на складе обновляются ежемесячно и составляют 70 Математическая постановка задачи. Пусть
При этом линейная функция Стандартный вид min (Z= -6x1-5x2-4x3-3x4) 2x1+3x2+2x3+x4+S1=25 4x1+x2+3x3+2x4+S2=30 3x1+5x2+2x3+2x4+S3=42 x1, x2, x3, x4, S1, S2, S3 > 0
Анализ решения Продукции 1 вида производим 6,5 ед., второго вида 4 единицы, третьего и четвертого вообще не производим. Прибыль при этом составит 59 ден. единиц. Ресурс 1 типа стоит 1,4 ден. ед., 2 типа – 0,8 ден. ед. Третий тип ресурса у нас остался в количестве 2,5 ед., поэтому его покупать не нужно.
Ресурсы 1 и 2 типа дефицитны, 3 типа избыточен. Эффективность производства: Z = 6*6.5+5*4+4*0+3*0=59 Z*=25*1.4+30*0.8+42*0=59 Производство в целом эффективно 2*1,4+4*0,8+3*0 < 6 6=6 Производство 1 вида продукции эффективно 3*1,4+1*0,8+5*0 < 5 5=5 Производство 2 вида продукции эффективно 2*1,4+3*0,8+2*0 < 4 5,2> 4 Производство 3 вида продукции не эффективно 1*1,4+2*0,8+2*0 < 3 3=3 Т.к. x4 не входит в базис, то оптимальный план не единственен. Оценить целесообразность покупки 5 ед. второго ресурса по цене 10 ден. ед, т.е. единица ресурса обойдется нам в 2 ден. ед. Мы же готовы покупать только по 0,8 ден. ед. за 1 единицу ресурса. а1 = 2, а2 = 2, а3 = 4. Цена новой продукции равна 4. 2*1,4+2*0,8+2*0 < 4 4,4> 4 Производство 5 вида продукции не эффективно. Пример. Для изготовления продукции используют 3 вида сырья. При этом можно применять любой из четырех способов производства. Запасы сырья, расход и количество производимой продукции за 1 час работы по каждому способу приведены в таблице.
Требуется найти план производства, при котором будет выпущено наибольшее количество продукции. Обозначим через
Эту задачу сведём к канонической задаче минимизации:
Cоставим симплекс-таблицу. Симплекс-таблица оказывается приведённой к базису
Выбираем положительную
Базис
Все оценки базиса Транспортная задача Транспортная задача относится к классу задач линейного программирования. Она решает проблему нахождения оптимального, минимального по стоимости плана распределения и перемещения ресурсов от производителя к потребителям. При решении транспортной задачи необходимо обеспечить всех потребителей ресурсами, распределить все произведенные ресурсы и переместить ресурсы от производителя к потребителю с наименьшими затратами.
Транспортная задача разрешима, когда количество произведенного ресурса равно количеству потребленного ресурса. Такая задача называется сбалансированной или закрытой. В реальных условиях такая задача достаточно редкая. Чаще встречаются ситуации, когда произведено ресурсов больше, чем его могут потребить – это избыток ресурсов. Или заказов на ресурс больше, чем выпускает изготовитель – это дефицит ресурса. Задачи в таких случаях решаются следующим образом: в задачу добавляют фиктивного потребителя или фиктивного изготовителя и находят оптимальное решение. Такие задачи называют несбалансированными или открытыми. Транспортная задача тогда будет разрешима и может иметь единственное решение, несколько допустимых, одно из которых оптимально или несколько допустимых и все они оптимальные. Алгоритм решения: 1. Формализация задачи составления матрицы стоимости перевозок; 2. Приведение задачи к сбалансированному виду; 3. Построение опорного плана; 4. Построение оптимального плана. Метод наименьшего элемента 1) Сбалансировать задачу (убедиться, что задача сбалансирована). 2) Определить свободную клетку с наименьшей стоимостью перевозки. Если таких клеток несколько, то выбрать клетку с наибольшей потенциальной грузоперевозкой. Если и таких клеток несколько, то выбирается любая из этих клеток. 3) В выбранную клетку поставить максимально возможную грузоперевозку для потребителя от поставщика. 4) Проверить, остался ли нераспределенным груз у этого поставщика. 5) Если груз распределен не полностью, то применяем п.2 относительно строки этого поставщика. Продолжать до тех пор, пока груз этого поставщика будет полностью распределен. Если груз поставщика распределен полностью, проверить, полностью ли удовлетворен объем потребителя. Если потребитель полностью удовлетворен, то применить пункт 2 относительно оставшихся поставщиков и потребностей в таблице. Если объем потребителя полностью не удовлетворен, тогда применяется пункт 2 относительно соответствующего столбца. 6) Проверить план на вырожденность. Количество базисных клеток должно быть равным r=m+n-1. Если план вырожденный, то поставить фиктивное значение груза так, чтобы иметь возможность найти потенциалы всех базисных клеток (ставить нулевую перевозку). 7) Проверить на оптимальность и по возможности дальше улучшить, перейдя к методу потенциалов.
Метод потенциалов 1) Для всех базисных клеток создать систему уравнений вида Выбрать переменную Ui или Vj, которой соответствует наибольшее количество занятых клеток, приравнять её к нулю, решить систему уравнений относительно Ui и Vj и найти эти значения. 2) Для всех свободных клеток составить и проверить выполнение неравенств: Условия оптимальности: если для всех свободных клеток выполняется это неравенство, то тогда найден оптимальный план. Если хотя бы для одной клетки не выполняется это неравенство, то необходимо улучшить опорный план с помощью коэффициента перераспределения W. 3) Находим клетку, где сильнее всего не выполняется неравенство. Если таких клеток несколько, то выбирается любая. В эту клетку ставим W со знаком «+». 4) Построить контур перераспределения груза, начиная с выбранной клетки, исходя из следующих правил: - В строке и столбце должно быть четное число W; - Контур меняет направление только в базисных клетках; - Коэффициент W меняет свой знак с «+» на «-» поочередно в углах контура. 5) После построения контура отметить, в каких базисных клетках коэффициент W стоит с отрицательным знаком. Из этих клеток найти клетку с наименьшим значением перевозки, коэффициент W будет равен перевозке в выбранной клетке. 6) Найти новый план, перераспределив найденное значение W по контуру с учетом знаков «+» и «-», прибавляя или уменьшая стоящую в клетке перевозку. 7) Проверить новый план в соответствии в п.2. если неравенства для свободных клеток выполняются, значит найденный план оптимален. Если в математической модели целевая функция на максимум (Zmax), то задача решается методом максимального элемента. т.е. грузоперевозка (Xij) распределяется при составлении опорного плана с учетом наибольшего значения Cij аналогично метода наименьшего элемента. В методе потенциалов проверяется выполнение неравенства Примеры решения транспортных задач Пример 1. Студенческие отряды СО-1, СО-2 и СО-3 численностью 70, 99 и 80 человек принимают участие в сельскохозяйственных работах. Для уборки картофеля на полях П1, П2, П3 и П4 необходимо выделить соответственно 47, 59, 49 и 43 человека. Производительность труда студентов зависит от урожайности картофеля, от численности отряда и характеризуется для указанных отрядов и полей в центнерах на человека за рабочий день и представлена в матрице:
Требуется: Распределить студентов по полям так, чтобы за рабочий день было собрано максимально возможное количество картофеля; Определить, сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении студентов Решение: Проверяем задачу на сбалансированность. Общее количество человек в студенческих отрядах на 51 больше требуемого общего количества человек для уборки картофеля. Задача является не сбалансированной. Чтобы сбалансировать задачу, добавляем фиктивное картофельное поле, для уборки которого нужно выделить 51 человека. Производительность труда студентов на фиктивном поле принимаем равной НУЛЮ.
Составляем исходную таблицу
Обозначения: П5 – фиктивное картофельное поле; С ij – производительность труда студентов i -го СО на j – м картофельном поле; Xij – количество студентов, направляемое из i -го СО на j-ое картофельное поле; Ui – условные оценки СО; Vj – условные оценки картофельных полей Составляем математическую модель прямой и двойственной задач. Математическая модель прямой задачи: Целевая функция (на максимум)
Система ограничений:
Математическая модель двойственной задачи.
Решаем задачу по методу максимального элемента. Составляем опорный план
СО-1 | 70 | 3 | 59 7 | 2 | 11 – W | + W | U1 =-1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СО-2 | 99 | 18 -W | 49 | 32 | + W 6 | 0 | U2= 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СО-3 | 80 | 29 | +W | 51 | -W | U3 =4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 4 | 3 | 5 |
0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vj | V1 =2 | V2 =8 | V3 =4 | V4 =6 | V5 = -4 | W=11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверяем на вырожденность.
Z= m+n-1=3+5-1=7
Базисных клеток 7. План не вырожден.
Проверяем опорный план на оптимальность.
Задаем U2 = 0 и определяем значения потенциалов.
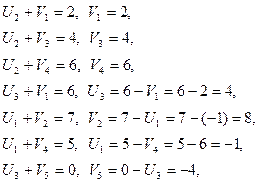
Вычисляем оценки для всех незаполненных клеток (D ij)
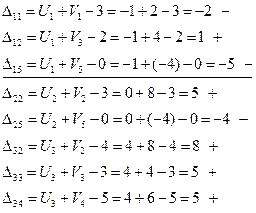
Опорное решение не является оптимальным, так как имеются отрицательные оценки.
Переходим к следующему плану.
Для клетки (1,5) с наименьшей оценкой (-5) строим цикл. Ставим в эту клетку коэффициент W со знаком «+» и применяя метод наибольшего элемента находим цикл, (табл. 2). Определяем из цикла W =11
Осуществляем сдвиг по циклу и строим следующий план
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |||
| 47 | 59 | 49 | 43 | 51 | |||||
СО-1
70
3
59
7
2
11
U1 =4
0
СО-2
99
7 -W
+W
U2= 0
СО-3
80
U3 =4
6
0
Vj
V1 =2
V5 = -4
Проверяем план на оптимальность методом максимального элемента, как в п.З.
Задаем U2 = 0 и определяем значения потенциалов.
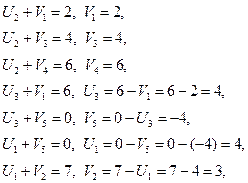
Вычисляем оценки для всех незаполненных клеток (D ij)
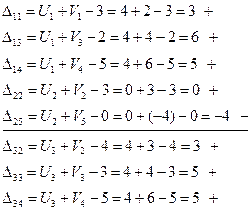
Определяем из цикла W=7
Осуществляем сдвиг по циклу и строим следующий план.
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |
| 47 | 59 | 49 | 43 | 51 | |||
|
СО-1 | 70 | 3 | 59 7 | 2 | 11 | U1 =0 | |
| 5 | 0 | ||||||
| СО-2 | 99 | 2 | 3 | 49 4 | 43 6 | 7 0 | U2= 0 |
| СО-3 | 80 | 47 6 | 4 | 3 | 5 | 33 0 | U3 =0 |
| Vj | V1 =6 | V2 =7 | V3 =4 | V4 =6 | V5 = 0 | ||
Проверяем план на оптимальность методом максимального элемента.
Задаем U2 = 0 и определяем значения потенциалов.
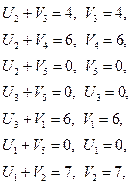
Вычисляем оценки для всех незаполненных клеток (D ij)
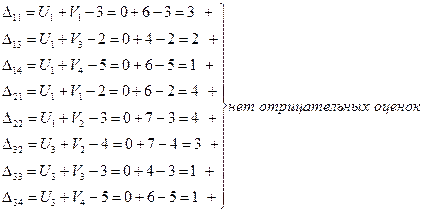
план оптимален.
Определяем значение целевой функции прямойидвойственной задачи:
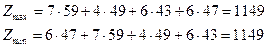
Исходя из первой теоремы двойственности в условии нашей задачи Zmax=Zmin=1149 (Z=Z’) последний план оптимален
Ответ:
1) Чтобы за рабочий день было убрано максимально возможное количество картофеля, следует распределить студентов по полям следующим образом:
– Из СО-1 выделить 59 человек для уборки картофеля на втором поле П2, а 11 человек останутся в СО;
– из СО-2 выделить 49 человек для уборки картофеля на ПЗ и 43 человека для уборки картофеля на П4, а 7 человек останутся в СО;
– из СО-3 выделить 47 человек для уборки картофеля на П1, а 33 человека оставить в СО.
2) При данном оптимальном распределении студентов с четырех полей будет убрано 1149 центнеров картофеля.
Схема гибели и размножения
Большинство реальных процессов, протекающих в технике, экономике, транспорте, можно описать с помощью размеченного графа специального вида:
λ12 λ23 λ34 λn-1, n
|

|


|
|
 …
…
λ21 λ32 λ43 λn, n-1
Особенностью данного графа является то, что каждое состояние, кроме первого и последнего связано только предыдущим и последующим состоянием.
Вычислим финальные вероятности событий:
1. Для события S 1: λ 12 p1= λ21p2
2. Для события S 2: (λ 23 + λ 21) p 2 = λ 12 p 1 + λ 32 p 3
Выполним преобразования:
λ23p2= λ32p3.
3. для события S 3: λ 32 p 3 = λ 43 p 4
4. Для события Sn: λn -1, n pn -1 = λn , n -1 pn.
Получим систему линейных уравнений:
 λ12 p1= λ21 p2
λ12 p1= λ21 p2
λ23 p2= λ32 p3
…
λn-1, n pn-1= λn, n-1 pn
Используя условие p1+ p2+ pn=1 (2) из первого уравнения выразим p2 через p1:

Из второго уравнения выразим p3 через p1:
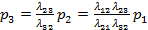 (3)
(3)
В числителе формулы (3) стоит произведение интенсивности потоков событий с увеличивающимся номером событий. В знаменателе – произведение интенсивности потоков событий с уменьшающимся номером событий.
После выполнения указанных действий все интенсивности событий выражены через одну вероятность p1.
Используя выражение (2) преобразуем формулу (3) к виду:

 (4)
(4)
Остальные вероятности можно вычислить, используя выражение (4), подставляя необходимое количество членов ряда в знаменателе.
Классификация СМО

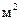
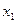 ,
, 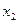 ,
, 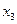 — месячный выпуск продукции соответственно: «стенок», «шкафов» и «гарнитуров» (
— месячный выпуск продукции соответственно: «стенок», «шкафов» и «гарнитуров» (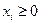 ,
, 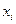 — целые,
— целые, 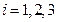 ). Тогда должно быть:
). Тогда должно быть: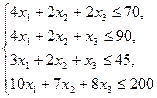
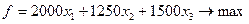
 Способ производства
Сырьё
Способ производства
Сырьё
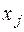 время использования j- го способа производства (j= 1,2,3,4), получим задачу линейного программирования:
время использования j- го способа производства (j= 1,2,3,4), получим задачу линейного программирования: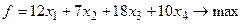
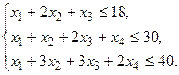
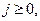
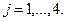 .
.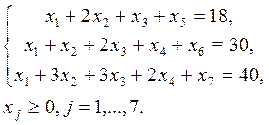
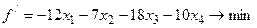
 опорного решения
опорного решения 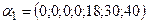 .
.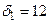 и составляем следующие отношения:
и составляем следующие отношения: 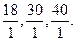 Так как наименьшее среди них
Так как наименьшее среди них 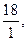 то необходимо перейти к базису
то необходимо перейти к базису 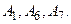 Для этого достаточно выполнить жорданово преобразование всей таблицы с ведущим элементом
Для этого достаточно выполнить жорданово преобразование всей таблицы с ведущим элементом 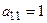 .
.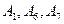 является базисом опорного решения
является базисом опорного решения 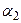 =(18;0;0;0;0;12;22). При этом
=(18;0;0;0;0;12;22). При этом 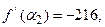 в то время как
в то время как 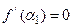 . Выбираем оценку
. Выбираем оценку 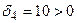 и составляем отношения
и составляем отношения 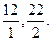 Наименьшим среди них является
Наименьшим среди них является 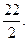 Следовательно, переходим к базису
Следовательно, переходим к базису 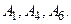 Получим таблицу.
Получим таблицу.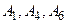 неположительны. Следовательно,
неположительны. Следовательно, 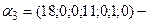 оптимальное решение канонической задачи минимизации. Поэтому
оптимальное решение канонической задачи минимизации. Поэтому 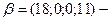 оптимальное решение исходной задачи. При этом
оптимальное решение исходной задачи. При этом 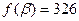 . Таким образом, для того чтобы выпустить наибольшее количество продукции при имеющихся запасах сырья, необходимо в течение 18 ч использовать первый способ производства и в течение 11 ч – четвертый. В результате будет произведено 326 единиц продукции.
. Таким образом, для того чтобы выпустить наибольшее количество продукции при имеющихся запасах сырья, необходимо в течение 18 ч использовать первый способ производства и в течение 11 ч – четвертый. В результате будет произведено 326 единиц продукции.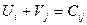 .
.