
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель двойственной задачиСодержание книги
Поиск на нашем сайте min (Z*= 25y1+30y2+42y3) 2y1+4y2+3y3 > 6 3y1+y2+5y3 > 5 2y1+3y2+2y3 > 4 y1+2y2+2y3 > 3 y1, y2, y3, y4 > 0
Стандартный вид min (Z= -6x1-5x2-4x3-3x4) 2x1+3x2+2x3+x4+S1=25 4x1+x2+3x3+2x4+S2=30 3x1+5x2+2x3+2x4+S3=42 x1, x2, x3, x4, S1, S2, S3 > 0
Экономический смысл переменных Xi – количество произведенной продукции Yj – цена ресурса Si – количество оставшегося ресурса
Анализ решения Продукции 1 вида производим 6,5 ед., второго вида 4 единицы, третьего и четвертого вообще не производим. Прибыль при этом составит 59 ден. единиц. Ресурс 1 типа стоит 1,4 ден. ед., 2 типа – 0,8 ден. ед. Третий тип ресурса у нас остался в количестве 2,5 ед., поэтому его покупать не нужно. Ресурсы 1 и 2 типа дефицитны, 3 типа избыточен. Эффективность производства: Z = 6*6.5+5*4+4*0+3*0=59 Z*=25*1.4+30*0.8+42*0=59 Производство в целом эффективно 2*1,4+4*0,8+3*0 < 6 6=6 Производство 1 вида продукции эффективно 3*1,4+1*0,8+5*0 < 5 5=5 Производство 2 вида продукции эффективно 2*1,4+3*0,8+2*0 < 4 5,2> 4 Производство 3 вида продукции не эффективно 1*1,4+2*0,8+2*0 < 3 3=3 Т.к. x4 не входит в базис, то оптимальный план не единственен. Оценить целесообразность покупки 5 ед. второго ресурса по цене 10 ден. ед, т.е. единица ресурса обойдется нам в 2 ден. ед. Мы же готовы покупать только по 0,8 ден. ед. за 1 единицу ресурса. а1 = 2, а2 = 2, а3 = 4. Цена новой продукции равна 4. 2*1,4+2*0,8+2*0 < 4 4,4> 4 Производство 5 вида продукции не эффективно. Пример. Для изготовления продукции используют 3 вида сырья. При этом можно применять любой из четырех способов производства. Запасы сырья, расход и количество производимой продукции за 1 час работы по каждому способу приведены в таблице.
Требуется найти план производства, при котором будет выпущено наибольшее количество продукции. Обозначим через
Эту задачу сведём к канонической задаче минимизации:
Cоставим симплекс-таблицу. Симплекс-таблица оказывается приведённой к базису
Выбираем положительную
Базис
Все оценки базиса Транспортная задача Транспортная задача относится к классу задач линейного программирования. Она решает проблему нахождения оптимального, минимального по стоимости плана распределения и перемещения ресурсов от производителя к потребителям. При решении транспортной задачи необходимо обеспечить всех потребителей ресурсами, распределить все произведенные ресурсы и переместить ресурсы от производителя к потребителю с наименьшими затратами. Транспортная задача разрешима, когда количество произведенного ресурса равно количеству потребленного ресурса. Такая задача называется сбалансированной или закрытой. В реальных условиях такая задача достаточно редкая. Чаще встречаются ситуации, когда произведено ресурсов больше, чем его могут потребить – это избыток ресурсов. Или заказов на ресурс больше, чем выпускает изготовитель – это дефицит ресурса. Задачи в таких случаях решаются следующим образом: в задачу добавляют фиктивного потребителя или фиктивного изготовителя и находят оптимальное решение. Такие задачи называют несбалансированными или открытыми. Транспортная задача тогда будет разрешима и может иметь единственное решение, несколько допустимых, одно из которых оптимально или несколько допустимых и все они оптимальные. Алгоритм решения: 1. Формализация задачи составления матрицы стоимости перевозок; 2. Приведение задачи к сбалансированному виду; 3. Построение опорного плана; 4. Построение оптимального плана.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 x1
x1
 S2
S2
 x2
x2

 Способ производства
Сырьё
Способ производства
Сырьё
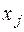 время использования j- го способа производства (j= 1,2,3,4), получим задачу линейного программирования:
время использования j- го способа производства (j= 1,2,3,4), получим задачу линейного программирования: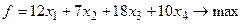
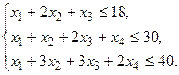
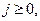
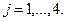 .
.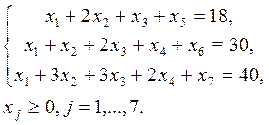
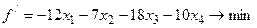
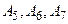 опорного решения
опорного решения 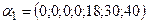 .
.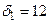 и составляем следующие отношения:
и составляем следующие отношения: 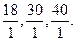 Так как наименьшее среди них
Так как наименьшее среди них 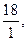 то необходимо перейти к базису
то необходимо перейти к базису 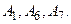 Для этого достаточно выполнить жорданово преобразование всей таблицы с ведущим элементом
Для этого достаточно выполнить жорданово преобразование всей таблицы с ведущим элементом 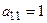 .
.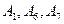 является базисом опорного решения
является базисом опорного решения 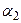 =(18;0;0;0;0;12;22). При этом
=(18;0;0;0;0;12;22). При этом 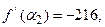 в то время как
в то время как 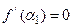 . Выбираем оценку
. Выбираем оценку 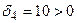 и составляем отношения
и составляем отношения 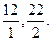 Наименьшим среди них является
Наименьшим среди них является 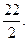 Следовательно, переходим к базису
Следовательно, переходим к базису 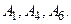 Получим таблицу.
Получим таблицу.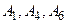 неположительны. Следовательно,
неположительны. Следовательно, 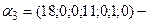 оптимальное решение канонической задачи минимизации. Поэтому
оптимальное решение канонической задачи минимизации. Поэтому 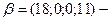 оптимальное решение исходной задачи. При этом
оптимальное решение исходной задачи. При этом 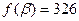 . Таким образом, для того чтобы выпустить наибольшее количество продукции при имеющихся запасах сырья, необходимо в течение 18 ч использовать первый способ производства и в течение 11 ч – четвертый. В результате будет произведено 326 единиц продукции.
. Таким образом, для того чтобы выпустить наибольшее количество продукции при имеющихся запасах сырья, необходимо в течение 18 ч использовать первый способ производства и в течение 11 ч – четвертый. В результате будет произведено 326 единиц продукции.


