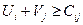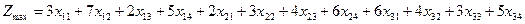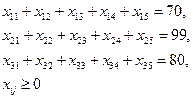Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая формулировка транспортной задачиСодержание книги
Поиск на нашем сайте
От каждого i-того производителя, произведенный им ресурс ai может перемещаться к j-тому потребителю ресурса в объеме, не превышающим bj. Таким образом xij будет означать, перемещение некоторого числа единиц ресурса от i-того производителя к j-тому потребителю. cij обозначим стоимость перемещения единицы ресурса, тогда матрица X={xij} будет называться матрицей или планом перевозок, C={cij} – матрицей стоимости. Любой план перевозок X, обеспечивающий распределение ресурсов между потребителями будет допустимым. Суммарная стоимость всех перевозок, вычисленная по любому допустимому плану, будет равна Оптимальным планом перевозок X* будет называться тот из допустимых планов перевозок, который обеспечивает минимальную сумму затрат на перевозку всех ресурсов. Исходные данные транспортной задачи задаются вектором произведенных ресурсов A = {ai}, вектором потребления ресурсов bj, и матрицей стоимости C, где 1<i<n, 1<j<m. n – общее число производителей, m – общее число потребителей. Математическая модель транспортной задачи
При заданных ограничениях:
Метод наименьшего элемента 1) Сбалансировать задачу (убедиться, что задача сбалансирована). 2) Определить свободную клетку с наименьшей стоимостью перевозки. Если таких клеток несколько, то выбрать клетку с наибольшей потенциальной грузоперевозкой. Если и таких клеток несколько, то выбирается любая из этих клеток. 3) В выбранную клетку поставить максимально возможную грузоперевозку для потребителя от поставщика. 4) Проверить, остался ли нераспределенным груз у этого поставщика. 5) Если груз распределен не полностью, то применяем п.2 относительно строки этого поставщика. Продолжать до тех пор, пока груз этого поставщика будет полностью распределен. Если груз поставщика распределен полностью, проверить, полностью ли удовлетворен объем потребителя. Если потребитель полностью удовлетворен, то применить пункт 2 относительно оставшихся поставщиков и потребностей в таблице. Если объем потребителя полностью не удовлетворен, тогда применяется пункт 2 относительно соответствующего столбца. 6) Проверить план на вырожденность. Количество базисных клеток должно быть равным r=m+n-1. Если план вырожденный, то поставить фиктивное значение груза так, чтобы иметь возможность найти потенциалы всех базисных клеток (ставить нулевую перевозку). 7) Проверить на оптимальность и по возможности дальше улучшить, перейдя к методу потенциалов.
Метод потенциалов 1) Для всех базисных клеток создать систему уравнений вида Выбрать переменную Ui или Vj, которой соответствует наибольшее количество занятых клеток, приравнять её к нулю, решить систему уравнений относительно Ui и Vj и найти эти значения. 2) Для всех свободных клеток составить и проверить выполнение неравенств: Условия оптимальности: если для всех свободных клеток выполняется это неравенство, то тогда найден оптимальный план. Если хотя бы для одной клетки не выполняется это неравенство, то необходимо улучшить опорный план с помощью коэффициента перераспределения W. 3) Находим клетку, где сильнее всего не выполняется неравенство. Если таких клеток несколько, то выбирается любая. В эту клетку ставим W со знаком «+». 4) Построить контур перераспределения груза, начиная с выбранной клетки, исходя из следующих правил: - В строке и столбце должно быть четное число W; - Контур меняет направление только в базисных клетках; - Коэффициент W меняет свой знак с «+» на «-» поочередно в углах контура. 5) После построения контура отметить, в каких базисных клетках коэффициент W стоит с отрицательным знаком. Из этих клеток найти клетку с наименьшим значением перевозки, коэффициент W будет равен перевозке в выбранной клетке. 6) Найти новый план, перераспределив найденное значение W по контуру с учетом знаков «+» и «-», прибавляя или уменьшая стоящую в клетке перевозку. 7) Проверить новый план в соответствии в п.2. если неравенства для свободных клеток выполняются, значит найденный план оптимален. Если в математической модели целевая функция на максимум (Zmax), то задача решается методом максимального элемента. т.е. грузоперевозка (Xij) распределяется при составлении опорного плана с учетом наибольшего значения Cij аналогично метода наименьшего элемента. В методе потенциалов проверяется выполнение неравенства Примеры решения транспортных задач Пример 1. Студенческие отряды СО-1, СО-2 и СО-3 численностью 70, 99 и 80 человек принимают участие в сельскохозяйственных работах. Для уборки картофеля на полях П1, П2, П3 и П4 необходимо выделить соответственно 47, 59, 49 и 43 человека. Производительность труда студентов зависит от урожайности картофеля, от численности отряда и характеризуется для указанных отрядов и полей в центнерах на человека за рабочий день и представлена в матрице:
Требуется: Распределить студентов по полям так, чтобы за рабочий день было собрано максимально возможное количество картофеля; Определить, сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении студентов Решение: Проверяем задачу на сбалансированность. Общее количество человек в студенческих отрядах на 51 больше требуемого общего количества человек для уборки картофеля. Задача является не сбалансированной. Чтобы сбалансировать задачу, добавляем фиктивное картофельное поле, для уборки которого нужно выделить 51 человека. Производительность труда студентов на фиктивном поле принимаем равной НУЛЮ.
Составляем исходную таблицу
Обозначения: П5 – фиктивное картофельное поле; С ij – производительность труда студентов i -го СО на j – м картофельном поле; Xij – количество студентов, направляемое из i -го СО на j-ое картофельное поле; Ui – условные оценки СО; Vj – условные оценки картофельных полей Составляем математическую модель прямой и двойственной задач. Математическая модель прямой задачи: Целевая функция (на максимум)
Система ограничений:
Математическая модель двойственной задачи.
Решаем задачу по методу максимального элемента. Составляем опорный план
СО-1 | 70 | 3 | 59 7 | 2 | 11 – W | + W | U1 =-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СО-2 | 99 | 18 -W | 49 | 32 | + W 6 | 0 | U2= 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 3 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
СО-3 | 80 | 29 | +W | 51 | -W | U3 =4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 4 | 3 | 5 |
0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vj | V1 =2 | V2 =8 | V3 =4 | V4 =6 | V5 = -4 | W=11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Проверяем на вырожденность.
Z= m+n-1=3+5-1=7
Базисных клеток 7. План не вырожден.
Проверяем опорный план на оптимальность.
Задаем U2 = 0 и определяем значения потенциалов.
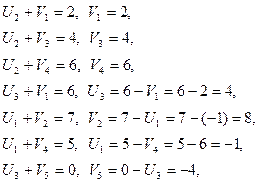
Вычисляем оценки для всех незаполненных клеток (D ij)
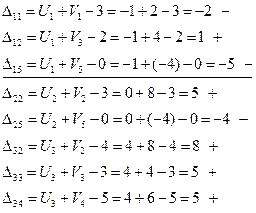
Опорное решение не является оптимальным, так как имеются отрицательные оценки.
Переходим к следующему плану.
Для клетки (1,5) с наименьшей оценкой (-5) строим цикл. Ставим в эту клетку коэффициент W со знаком «+» и применяя метод наибольшего элемента находим цикл, (табл. 2). Определяем из цикла W =11
Осуществляем сдвиг по циклу и строим следующий план
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |||
| 47 | 59 | 49 | 43 | 51 | |||||
СО-1
70
3
59
7
2
11
U1 =4
0
СО-2
99
7 -W
+W
U2= 0
СО-3
80
U3 =4
6
0
Vj
V1 =2
V5 = -4
Проверяем план на оптимальность методом максимального элемента, как в п.З.
Задаем U2 = 0 и определяем значения потенциалов.
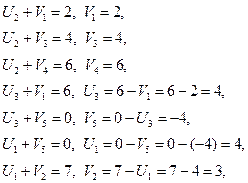
Вычисляем оценки для всех незаполненных клеток (D ij)
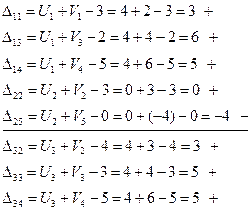
Определяем из цикла W=7
Осуществляем сдвиг по циклу и строим следующий план.
| Bj Ai | П1 | П2 | П3 | П4 | П5 | Ui | |
| 47 | 59 | 49 | 43 | 51 | |||
|
СО-1 | 70 | 3 | 59 7 | 2 | 11 | U1 =0 | |
| 5 | 0 | ||||||
| СО-2 | 99 | 2 | 3 | 49 4 | 43 6 | 7 0 | U2= 0 |
| СО-3 | 80 | 47 6 | 4 | 3 | 5 | 33 0 | U3 =0 |
| Vj | V1 =6 | V2 =7 | V3 =4 | V4 =6 | V5 = 0 | ||
Проверяем план на оптимальность методом максимального элемента.
Задаем U2 = 0 и определяем значения потенциалов.
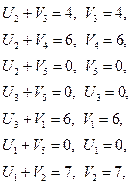
Вычисляем оценки для всех незаполненных клеток (D ij)
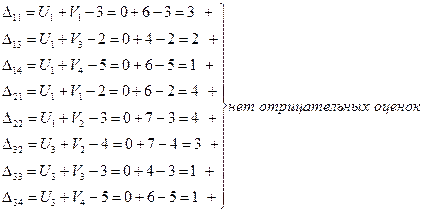
план оптимален.
Определяем значение целевой функции прямойидвойственной задачи:
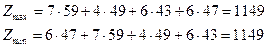
Исходя из первой теоремы двойственности в условии нашей задачи Zmax=Zmin=1149 (Z=Z’) последний план оптимален
Ответ:
1) Чтобы за рабочий день было убрано максимально возможное количество картофеля, следует распределить студентов по полям следующим образом:
– Из СО-1 выделить 59 человек для уборки картофеля на втором поле П2, а 11 человек останутся в СО;
– из СО-2 выделить 49 человек для уборки картофеля на ПЗ и 43 человека для уборки картофеля на П4, а 7 человек останутся в СО;
– из СО-3 выделить 47 человек для уборки картофеля на П1, а 33 человека оставить в СО.
2) При данном оптимальном распределении студентов с четырех полей будет убрано 1149 центнеров картофеля.
|
| Поделиться: |

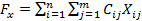
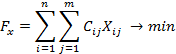
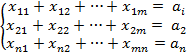
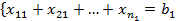
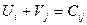 .
.