
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование систем массового обслуживанияСодержание книги
Поиск на нашем сайте
На любую систему массового обслуживания воздействует два потока событий: входной поток и выходной. В установившемся режиме среднее число входящих событий за единицу времени равно среднему числу выходящих событий и оба потока имеют одну и ту же интенсивность λ=1/ T. Обозначим через x(T) количество внешних событий за время Т через y(T) количество обслуженных событий. В момент времени t1 и t4 обслуживается одно событие. В момент времени t2 обслуживается два события, а в t3 заявок нет, и каналы прислуживания простаивают. Z(t)= X(t)- Y(t) представляет собой количество событий, которое обслуживается СМО в момент времени Т. Если t стремится к бесконечности, что среднее число входящих в СМО событий определяется по формуле:
где,
Т. е. для любой системы среднее время обслуживания системы равно среднему числу событий, деленному на интенсивность входного потока событий (λ). Время ожидания
Классификация СМО 1. Одноканальные СМО с неограниченной очередью – такие системы можно представить с помощью графа: λ λ λ λ
μ μ μ μ
Под неограниченной очередью понимается количество заявок, поступивших на обслуживание. Время обслуживания каждой заявки неограниченное и произвольное, но все заявки рано или поздно будут обслужены. Каждая вновь поступившая заявка будет переводить систему в новое состояние S с увеличением индекса на 1, а каждая выполненная заявка будет уменьшать состояние S на 1. Т. к система обслуживает только одну заявку, то Длина очереди Среднее время пребывания заявки в очереди
Среднее время пребывания заявки в очереди: 2. Одноканальные СМО с ограниченной очередью – в отличие от предыдущей системы, после поступления n-й заявки, всем остальным заявкам будет отказано в обслуживании и они покинут систему. λ λ λ
μ μ μ Вычисление характеристик выполняется по тем же формулам, что и в предыдущей системе, но учитывается конечное количество членов геометрической прогрессии. 3. Многоканальные СМО с ограниченной очередью. Обозначим характеристики: p0 – вероятность простоев каналов обслуживания; pотк – вероятность отказа каналов обслуживания; pобс – вероятность обслуживания; nz – среднее число каналов, занятых обслуживанием kz – доля каналов, занятых обслуживанием. A – абсолютная пропускная способность, т. е. среднее количество заявок, обслуженных за единицу времени. Q – относительная пропускная способность, т. е. среднее значение обслуженных заявок. λ λ λ λ
μ 2μ 3μ mμ (m+1)μ nμ
Данная система имеет n-каналов с одинаковы техническими характеристиками и может находится в одном из состояний: S0 – заявки отсутствуют; S1 – поступила одна заявка и она обслуживается первым каналом, остальные каналы простаивают; S2 –во время выполнения первой заявки поступила вторая заявка, вторая заявка обслуживается вторая, остальные каналы простаивают. Sn – во время выполнения n-1 заявок поступила заявка n, которая облаживается n-ым каналом. Все каналы заняты. Последующим заявкам будет отказано в обслуживании.
Заявки на обслуживание поступают произвольно с интенсивностью λ. При поступлении второй заявки ее обрабатывает второй канал, и интенсивность обслуживания удваивается, т. е. становится равной 2μ.
Финальная вероятность события S0: Относительная пропускная способность: Абсолютная пропускная способность: Среднее количество занятых кагалов: 4. Многоканальные СМО с неограниченной очередью. λ λ λ λ λ λ λ λ
μ 2μ 3μ mμ (m+1)μ nμ nμ nμ nμ nμ
S0 – заявки отсутствуют … Sn – все каналы заняты Sn+1 – вновь поступившая заявка встает в очередь и ожидает обслуживания. Все последующие заявки также встают в очередь. Для такой системы должно выполняться условие: Число занятых каналов: Среднее число обслуживаемых заявок Среднее время обслуживания: Среднее время ожидания:
Пример 1. Дежурный администратор города имеет 5 телефонов. Звонки поступают с интенсивностью 90 звонков/час. Средняя продолжительность разговора составляет 2 мин. Определить характеристики дежурного администратора как системы массового обслуживания. Решение: 1. Классифицируем СМО: · с отказами (нет накопителя); · многоканальная (5 телефонов = 5 каналов). 2. Обозначения: λ – интенсивность потока заявок (λ=90зв/60мин=3зв/2мин) n – число каналов (n=5); μ – интенсивность потока обслуживания, т.е. среднее число заявок, обслуживаемых в единицу времени (μ=1/ tобс) tобс – среднее время обслуживания (tобс=2мин) ρ – интенсивность нагрузки; k – номер заявки (число заявок), k=n=5; Р0 – вероятность простоя каналов обслуживания, когда нет заявок; Ротк – вероятность отказа в обслуживании, когда поступившая на обслуживание заявка найдет все каналы занятыми; Робс – вероятность обслуживания. nз = ρ* Робс - среднее число занятых обслуживанием каналов. кз = nз / n - для каналов, занятых обслуживанием. А = λ Робс - абсолютная пропускная способность СМО. 3. Определяем характеристики данной СМО: а) ρ = λ/μ = λ/(1/tобс) = λ tобс = 3/2 * 2 = 3 б) =1/ (1+3/1)+(3*3/1*2)+(3*3*3/1*2*3)+(3*3*3*3/1*2*3*4)+(3*3*3*3*3/1*2*3*4*5) =1/ 1+3+(9/2)+(27/6)+(81/24)+(243/120)=0,054 в) г) Робс = 1- Ротк = 1-0,12=0,88 д) nз = ρ*Робс = 3*0,88=2,6 е) кз = nз / n = 2,6/5=0,52 ж) А = λ Робс = (3/2)*0,88 = 1,31.
Пример № 2. На автомобильной стоянке возле магазина имеется 2 места. Рядом находится площадка на 2 а/м. На стоянку прибывает 1 машина в 3 мин. Среднее время нахождения водителя в магазине 2 мин. Определить характеристики этой СМО. Решение: 1. Классифицируем СМО: - с ограниченной длиной очереди - с накопителем - многоканальная - с ограничением общего времени пребывания заявки в системе СМО с ожиданием и с ограниченной длиной очереди. 2. Обозначения: m=2 - длина накопителя n=2 - число каналов Остальные обозначения - как в Примере № 1. 3. Определяем характеристики данной СМО: а) λ = 1/3; б) tобс = 2 мин; в) ρ = λ/μ = λ/(1/tобс) = λ tобс = (1/3)*2=2/3. г) Вероятность простоя каналов: =1/ ((ρ0/0!)+(ρ1/1!)+(ρ2/2!)+(ρ2+1/1*2(2-ρ))*[1-(ρ/2)2]=1/ ((2/3)/0!)+2/3+((2/3)2/(1*2))+ +((2/3)3/ 2(2-2/3)) [1- ((2/3)/2)]= 1/ 1+2/3+2/9+1/9[1-1/9]=0,52 д) Вероятность отказа в обслуживании: е) Вероятность обслуживания: Робс = 1- Ротк = 0,987 ж) Абсолютная пропускная способность: А = λ Робс = 0,987*1/3=0,33 з) Среднее число занятых каналов: nз = ρ*Робс = 2/3*0,987=0,658 Для каналов, занятых обслуживанием: кз = 0,658/2=0,329. и) Среднее число заявок в очереди:
=(8/27)/4* * (1-1/9*7/3) /(4/9)= 2/27*((20/27)/(4/9))*0.52=2/27*5/3*0.52=0.14 к) Среднее время ожидания обслуживания: л) Среднее число заявок в системе: м) Среднее время пребывания в системе: tсмо= Z/ λ = 0,8/0,33=2,42 или tсмо= tor+ toбс = 0,42+2=2,42 мин ЛИТЕРАТУРА 1. Агальцов В.П. Математические методы в программировании. – М.: Издательский дом «ФОРУМ», 2010 2. Балдин К.В., Брызгалов Н.А., Рукосуев А.В. Математическое программирование. – М.: ИТК «Дашков и К», 2008 3. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование.– Изд. Лань, 2010 4. Кузнецов А.В., Сакович В.А., Холод Н.И. Сборник задач и упражнений по высшей математике. Математическое программирование.– Изд. Лань, 2010 5. Юденков А.В., Дли М.И., Круглов В.В. Математическое программирование в экономике. – М.: «Финансы и статистика», 2010 Интернет ресурсы:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.203 (0.005 с.) |

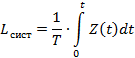

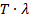 – среднее время пребывания события внутри системы, т. е. среднее время обслуживания системы.
– среднее время пребывания события внутри системы, т. е. среднее время обслуживания системы.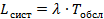
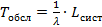
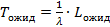
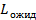 – среднее число событий в очереди.
– среднее число событий в очереди.
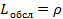
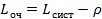
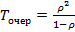
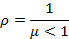
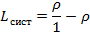
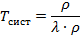
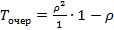

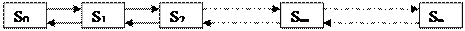
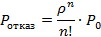
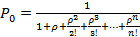
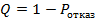
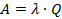
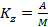

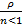
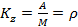
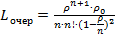
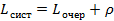
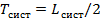
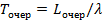
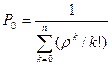 = 1/ (ρ0/0!)+(ρ1/1!)+(ρ2/2!)+(ρ3/3!)+(ρ4/4!)+(ρ5/5!) =
= 1/ (ρ0/0!)+(ρ1/1!)+(ρ2/2!)+(ρ3/3!)+(ρ4/4!)+(ρ5/5!) = 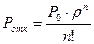 = (35/ 1*2*3*4*5)*0,054=(3*3*3*3*3/1*2*3*4*5)*0,054=(243/120)*0,054=0,12
= (35/ 1*2*3*4*5)*0,054=(3*3*3*3*3/1*2*3*4*5)*0,054=(243/120)*0,054=0,12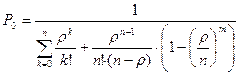 =
=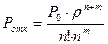 = ((2/3)4/1*2*22)*0,52 =(16/81)/8*0,52=0,013
= ((2/3)4/1*2*22)*0,52 =(16/81)/8*0,52=0,013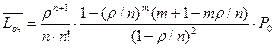
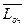 =( (2/3)3/(2*2) ) * 1- ( (2/3)/2)2 ) * ( 2+1-2*((2/3)/2) ) / ( 1-(2/3)/2)2 ) *0.52
=( (2/3)3/(2*2) ) * 1- ( (2/3)/2)2 ) * ( 2+1-2*((2/3)/2) ) / ( 1-(2/3)/2)2 ) *0.52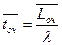 = 0.14/0.33=0.42
= 0.14/0.33=0.42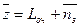 = 0,14+0,66=0,8
= 0,14+0,66=0,8


