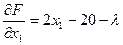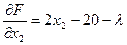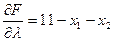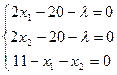Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение с помощью системы MathcadСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Зададим ЦФ: Z(x1, x2):= (х1-7)2+ (х2-4)2 Зададим произвольные начальные значения переменным: x1:= 0 x2:= 0 Начало блока вычислений Given Опишем ограничения: х1 + х2 ≤ 10 2х1 + х2 ≥ 12 х1 – х2 ≥ 2 х1 – х2 ≤ 4 х1 ≥ 0 х2 ≥ 0 Выполним операцию минимизации: P: = Minimize (Z, x1, x2) Выведем на экран значения найденных переменных:
Вычислим целевую функцию: Z (P0, P1) = 0.5 Итак, оптимальные значения переменных: х1 = 6,5, х2 = 3,5. Значение ЦФ Z = 0,5
Практическое занятие № 8 Наименование работы: Решение трехмерной задачи нелинейного программирования с помощью Mathcad Цель работы: Научиться решать задачи нелинейного программирования с помощью Mathcad. Формировать ОК 1 – ОК 9, овладеть знаниями и умениями, необходимыми для освоения ПК 1.1, ПК 1.2. Подготовка к занятию: Повторить теоретический материал по теме «Нелинейное программирование» Литература:
Перечень необходимых приборов, инструментов, материалов: ПЭВМ Задание на занятие: С помощью математической системы Mathcad максимизировать целевую функцию Z, приведенную в таблице в соответствии со своим вариантом. По результатам расчета построить трехмерный график, на котором изобразить поверхности ограничений и поверхность рассчитанной ЦФ. На графике показать точку оптимума.
Примечание. Во всех вариантах считать х1≥0, х2≥0, х3≥0. Порядок проведения занятия:
2. Выполнить задание в соответствии со своим вариантом. 3. Ответить на контрольные вопросы. Содержание отчета:
Контрольные вопросы для зачета: 1. Сформулируйте задачу нелинейного программирования в общем виде. 2. Опишите порядок решения задачи нелинейного программирования с помощью системы Mathcad. ПРИЛОЖЕНИЕ Пример выполнения задания с помощью системы Mathcad. Зададим ЦФ: Z(x1,x2, x3):= 3x1 + 4 х22 + 2x3 Зададим произвольные начальные значения переменным: x1:= 0 x2:= 0 x3:= 0 Начало блока вычислений Given Опишем ограничения: x1 ≥ 0 x2 ≥ 0 x3 ≥ 0 15 х12 + 16 х22-17 x3 ≤ 120 18 х12 + 19 х22+20 x3 ≤ 130 -21х12 + 22 х22+23 x3 ≤ 140 Выполним операцию максимизации: P: = Maximize(Z,x1,x2,x3) Выведем на экран значения найденных переменных:
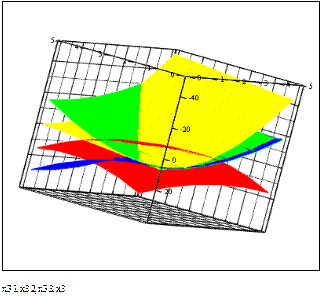
Вычислим целевую функцию: Z(P0, P1,P2) = 14.25 Итак, оптимальные значения переменных: х1 = 0.835, х2 = 0, x3 = 5,873. Максимальное значение ЦФ Z = 14.25 Построим трехмерный график, который показывает ограничения и оптимальное положение целевой функции. Присвоим значение ЦФ переменной R: R:= Z(P0, P1,P2) Создадим циклы для изменения переменных х1 и х2: x1:=0..P0 + 5 x2:=0..P1 + 5 Выразим переменную х3 из трех ограничений и целевой функции:
Графическая иллюстрация полученного решения
Практическое занятие № 9 Наименование работы: Решение задач нелинейного программирования методом множителей Лагранжа Цель работы: научиться решать задачи нелинейного программирования методом множителей Лагранжа. Формировать ОК 1 – ОК 9, овладеть знаниями и умениями, необходимыми для освоения ПК 1.1, ПК 1.2. Подготовка к занятию: Повторить теоретический материал по теме «Нелинейное программирование» Литература:
Перечень необходимых приборов, инструментов, материалов: ПЭВМ Задание на занятие: Решить двухмерную задачу минимизации целевой функции Z методом множителей Лагранжа и с помощью математической системы Mathcad. Сравнить результаты и сделать вывод.
Порядок проведения занятия: 1. Получить допуск к работе. 2. Выполнить задание в соответствии со своим вариантом. 3. Ответить на контрольные вопросы. Содержание отчета:
Контрольные вопросы для зачета: 1. Перечислите методы решения задач нелинейного программирования. 2. Опишите порядок решения задачи нелинейного программирования методом множителей Лагранжа.
ПРИЛОЖЕНИЕ
Рассмотрим частный случай общей задачи нелинейного программирования, предполагая, что система ограничений содержит только уравнения, отсутствуют условия отрицательности переменных и
Такую задачу называют задачей на условный экстремум или классической задачей оптимизации. Чтобы найти решение этой задачи, введем набор переменных
находим частные производные
с m + n неизвестными Таким образом, определение экстремальных точек задачи нелинейного программирования методом множителей Лагранжа включает следующие этапы: 1. Составляют функцию Лагранжа. 2. Находят частные производные от функции Лагранжа по переменным 3. Решая систему уравнений, находят точки, в которых целевая функция может иметь экстремум. 4. Среди точек, подозрительных на экстремум, находят точки, в которых достигается экстремум, и вычисляют значения целевой функции в этих точках.
Рассмотрим пример решения задачи нелинейного программирования методом множителей Лагранжа Пусть дана целевая функция Z = х12 - 20х1 - 20х2 + x22 с ограничениями: х 1 + х 2 = 11 х 1 ≥ 0, х 2 ≥ 0 Требуется минимизировать ЦФ.
Чтобы найти решение методом множителей Лагранжа, вначале следует сформировать функцию Лагранжа: F (х 1, х 2, λ) = х 12 - 20 х 1-20 х 2 + x 22+ λ (11- х 1 - х 2 ) Затем найдем производные по х 1, х 2, λ:
Далее найденные производные следует приравнять к нулю и решить полученную систему линейных алгебраических уравнений.
2 х 1 - 20 = 2 х 2 - 20 2 х 1 - 2 х 2 = 0 х 1 - х 2 = 0 х 1 + х 2 = 11 х 1 = 5.5 х 2 = 5.5 В ответ записываем значения х 1 = 5,5; х 2 = 5,5. Решение с помощью Mathcad осуществляется аналогично заданию из практического занятия 7.
Практическое занятие № 10 Наименование работы: Решение простейших задач методом динамического программирования Цель работы: научиться решать задачи методом динамического программирования. Формировать ОК 1 – ОК 9, овладеть знаниями и умениями, необходимыми для освоения ПК 1.1, ПК 1.2. Подготовка к занятию: Повторить теоретический материал по теме «Динамическое программирование» Литература:
Перечень необходимых приборов, инструментов, материалов: ПЭВМ Задание на занятие: Выделены денежные средства S0 =100 ден.ед. для вложения в инвестиционные проекты для реконструкции и модернизации производства на четырех предприятиях. По каждому предприятию известен возможный прирост fi(х)(i=1, 2, 3, 4) выпуска продукции в зависимости от выделенной суммы. Требуется распределить средства S0 между предприятиями так, чтобы суммарный прирост продукции на всех четырех предприятиях достиг максимальной величины. Параметр | Номер варианта | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f1 (20) | 4 | 2 | 4 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f2 (20) | 2 | 3 | 4 | 4 | 2 | 4 | 2 | 2 | 5 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f3 (20) | 4 | 4 | 4 | 5 | 2 | 3 | 4 | 1 | 4 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f4 (20) | 1 | 2 | 2 | 2 | 3 | 2 | 4 | 2 | 2 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f1 (40) | 4 | 4 | 6 | 6 | 7 | 6 | 3 | 4 | 3 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f2 (40) | 4 | 4 | 4 | 6 | 5 | 5 | 6 | 6 | 6 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f3 (40) | 6 | 3 | 3 | 4 | 6 | 3 | 4 | 4 | 3 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f4 (40) | 4 | 4 | 5 | 5 | 5 | 5 | 6 | 4 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f1 (60) | 9 | 7 | 9 | 8 | 7 | 9 | 5 | 6 | 4 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f2 (60) | 6 | 4 | 6 | 5 | 8 | 10 | 8 | 9 | 7 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f3 (60) | 10 | 8 | 5 | 6 | 5 | 10 | 5 | 4 | 9 | 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f4 (60) | 9 | 5 | 7 | 9 | 8 | 5 | 5 | 6 | 9 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f1 (80) | 12 | 11 | 7 | 11 | 12 | 7 | 11 | 7 | 7 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f2 (80) | 11 | 11 | 9 | 5 | 13 | 8 | 11 | 8 | 10 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f3 (80) | 5 | 8 | 8 | 12 | 7 | 7 | 12 | 7 | 6 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f4 (80) | 6 | 5 | 13 | 7 | 9 | 11 | 9 | 8 | 12 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f1 (100) | 15 | 14 | 14 | 14 | 14 | 15 | 11 | 15 | 14 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f2 (100) | 12 | 11 | 10 | 10 | 12 | 12 | 15 | 15 | 10 | 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f3 (100) | 12 | 13 | 13 | 10 | 10 | 12 | 11 | 10 | 12 | 15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f4 (100) | 13 | 14 | 12 | 13 | 14 | 14 | 13 | 12 | 14 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Порядок проведения занятия:
- Получить допуск к работе.
- Выполнить задание в соответствии с заданным вариантом.
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель работы, задание;
- Выполненное задание;
- Выводы по результатам выполненного задания;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
1. Какие задачи решаются методом динамического программирования?
2. Что означает понятие «шаговое управление»?
3. Как определяются шаги при решении задачи динамического программирования?
4. В чем суть принципа оптимальности Беллмана?
5. Каким образом проводится условная и безусловная оптимизация?
ПРИЛОЖЕНИЕ
Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги). Все шаги могут быть уникальными или одинаковыми и чередоваться друг с другом. Некоторые задачи оптимизации легко разделяются на шаги естественным способом, а для других вводится искусственное разделение на шаги.
Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.
Экономический процесс является управляемым, если можно влиять на ход его развития.
Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.
Операция– управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.
Решение на каждом шаге называется «шаговым управлением». Совокупность всех шаговых управлений представляет собой управление операцией в целом.
Примерами задач, решаемых методом динамического программирования, могут быть: распределение ресурсов (финансовых, сырьевых, материальных и т.д.) между предприятиями, замена или ремонт промышленного оборудования, прокладка коммуникаций (трубопроводов, дорог и т.д.) и пр. В этих задачах, как правило, в качестве шагов выступают отрезки времени, которые явно задаются в условии задачи.
Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:
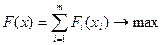
где F – выигрыш за операцию;
Fi(xi) – выигрыш на i-м шаге;
х – управление операцией в целом;
хi – управление на i-м шаге (i=1,2,…,m). В общем случае шаговые управления (х1, х2, … х m) могут стать числами, векторами, функциями.
То управление (х *), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управлений х* = х*1, х*2, … х*m
F* = max {F*(х*)} – максимальный выигрыш, который достигается при оптимальном управлении х*.
Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.
|
| Поделиться: |

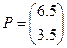
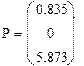
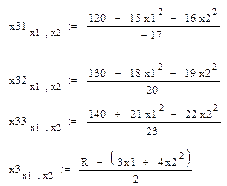
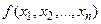 и
и 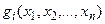 - функции, непрерывные вместе со своими частными производными (по крайней мере, вторая частная производная должна быть непрерывной).
- функции, непрерывные вместе со своими частными производными (по крайней мере, вторая частная производная должна быть непрерывной).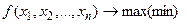
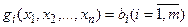
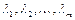 , называемых множителями Лагранжа, составим функцию Лагранжа
, называемых множителями Лагранжа, составим функцию Лагранжа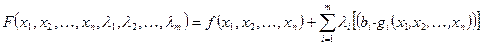 ,
,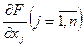 и
и 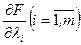 и рассматриваем систему
и рассматриваем систему 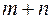 уравнений (здесь привлечём необходимое условие экстремума, заключающееся в том, что первая производная должна быть равна
уравнений (здесь привлечём необходимое условие экстремума, заключающееся в том, что первая производная должна быть равна 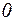 ):
):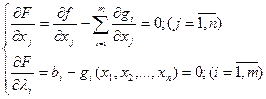
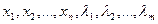 . Всякое решение системы уравнений определяет точку
. Всякое решение системы уравнений определяет точку 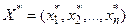 , в которой может иметь место экстремум функции
, в которой может иметь место экстремум функции 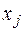 и
и 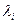 приравнивают их к нулю.
приравнивают их к нулю.