
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вводим матрицу стоимости перевозок, вектор запасов, вектор спросаСодержание книги
Поиск на нашем сайте
Вводим целевую функцию
xm,n:=0 Given
x ≥ 0 x:=Minimize(Z,x) Получим матрицу оптимальных перевозок
Определена стоимость оптимальных перевозок Z(x) =1330
Практическое занятие № 7 Наименование работы: Решение задач нелинейного программирования графическим методом Цель работы: Научиться решать задачи нелинейного программирования. Формировать ОК 1 – ОК 9, овладеть знаниями и умениями, необходимыми для освоения ПК 1.1, ПК 1.2. Подготовка к занятию: Повторить теоретический материал по теме «Нелинейное программирование» Литература:
Перечень необходимых приборов, инструментов, материалов: ПЭВМ Задание на занятие: Графически и аналитически решить задачу нелинейного программирования. Полученные результаты проверить с помощью математической системы Mathcad. Исходные данные необходимо выбрать из таблицы в соответствии со своим вариантом.
Порядок проведения занятия: 1. Получить допуск к работе. 2. Выполнить задание в соответствии со своим вариантом. 3. Ответить на контрольные вопросы. Содержание отчета:
Контрольные вопросы для зачета: 1. Сформулируйте задачу нелинейного программирования в общем виде. 2. Чем отличаются задачи нелинейного программирования от задач линейного программирования? 3. Перечислите основные этапы решения задачи нелинейного программирования графическим способом. 4. Где может быть расположена точка экстремума в задачах нелинейного программирования?
ПРИЛОЖЕНИЕ
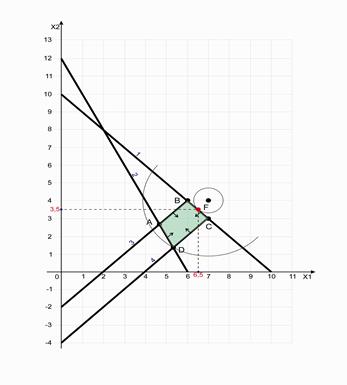
Требуется решить задачу нелинейного программирования тремя способами: графически, аналитически, с помощью математической системыMathcad.При решении нужно найти максимум и минимум целевой функции. Рассмотрим пример графического и аналитического решения задачи нелинейного программирования. Найдем минимум целевой функции: Z = (х1-7)2 + (х2-4)2 с ограничениями: х1+х2 ≤ 10, 2х1+х2 ≥ 12, х1-х2 ≥ 2, х1-х2 ≤ 4 х1≥ 0, х2≥ 0 Графическое решение Чтобы решить задачу графически, вначале следует изобразить многоугольник допустимых решений, построение которого осуществляется так же, как в задачах линейного программирования. Область, удовлетворяющая всем четырем неравенствам, будет областью допустимых решений (трапеция ABCD). . Теперь необходимо построить график ЦФ. Для этого следует отметить центр окружности. В данном примере х1 = 7 и х2 = 4. Затем с помощью циркуля нужно построить несколько окружностей, увеличивая радиус до тех пор, пока окружность не коснется какой либо точки ОДР. В этой точке будет минимум ЦФ. Далее следует найти наиболее удаленную от центра окружности точку ОДР. В этой точке будет максимум ЦФ. Из рисунка видно, что минимум ЦФ находится в точке F, а максимум – в точке D. Определим приближенно координаты точки F: х1 = 6,5, х2 = 3,5. Значение целевой функции в этой точке Z = 0,5. Приближенные значения координат точки D: х1 = 5,3, х2 = 1,4. Приближенное значение ЦФ в этой точке Z = 9,65.
Аналитическое решение На основании приближенного графического решения задачи НПР найдём аналитически точный ответ. Для этого, из уравнения целевой функции Z = (х 1-7)2+(х 2-4)2 найдем частные производные по х 1 и х 2: Производная по х 1: Z| = 2(х 1-7) + 2(х 2-4)∙ х 2| . Приравняем Z| =0. Затем выразим из этого уравнения производную х 2| : х 2| = -(х 1-7/ х 2-4). Определим тангенс угла наклона (производную) для прямой х 1+ х 2 = 10 х 2| = -1 -(х 1-7/ х 2-4) = - 1 х 1-7 = х 2-4 Решим систему уравнений
х 1+ х 2 = 10 2 х 1= 13, х 1= 6,5 х 2 = 3,5 Полученные значения х 1 и х 2 подставляем в ЦФ Z = (х 1-7)2+(х 2-4)2 Таким образом, минимальное значение ЦФ Z=0,5.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

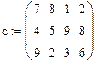
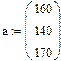
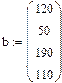
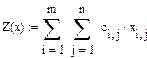
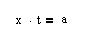
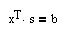
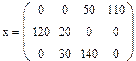
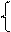 х 1 - х 2 = 3
х 1 - х 2 = 3



